固定式支承头点式玻璃的应力集中分析
2009-08-25董永刚
董永刚
[摘 要]利用有限元软件计算分析了固定式支承头点式玻璃孔边应力集中问题,具体讨论了孔径、孔心边距、玻璃几何尺寸、金属支承头的尺寸、垫层的厚度及物理力学性能等因素对孔边应力的影响,并给出了相应的建议。
[关键词]点式玻璃幕墙 固定式支承头 应力集中
一、概述
点式玻璃幕墙是最近几年在中国开始应用新型幕墙体系,由于其视野开阔、通透性强等优点得到了广泛应用。它由玻璃面板、金属连接件、支承结构等组成。由于点式支承玻璃技术在我国被采用的时间较短,资料还不够完备,它还很不成熟,尚有许多工作有待进行探讨和研究。玻璃是具有代表性的脆性材料,几乎所有的玻璃都是由于拉应力产生表面裂缝而破碎,它的应力应变几乎是呈线性关系,其破坏强度有非常大的离散性。点式玻璃幕墙采用钢化玻璃[1],它的强度和安全性能要优于普通玻璃和浮法玻璃。一般采用4点或6点支承。由于玻璃要开孔,因此玻璃孔周边将产生应力集中,这是点式玻璃的薄弱环节。孔边玻璃应力与支承点构造有关,也与玻璃孔洞加工工艺有关,这些因素的影响往往是不能忽略的。《规范》只是采用限制孔边距等条件来考虑孔边局部应力的影响[1,2],而设计人员往往对孔边应力集中的程度与危害了解不够,因此对孔边应力集中进行深入研究和探讨是必要的。点支玻璃的支承装置分活动式和固定式两种,活动式支承头在工程中应用较多,它允许玻璃板在孔边有部分转动,可有效地减缓孔边应力集中,这方面的资料可参考文献[3,4]。固定式支承头由于限制了板的转动,应力集中现象要严重得多[5]。虽然固定式支承头在工程中应用不多,但《规范》允许在工程中应用。本文主要探讨了玻璃面板在固定式支承头支承条件下,孔边的局部应力集中现象及其影响因素,并提出相应的建议。
二、计算模型
(一)计算模型
采用Ansys有限元分析软件进行分析,不考虑玻璃板自重对孔边应力的影响,采用1/4对称的计算模型,模型材料包括玻璃板,金属支承头和缓冲垫层。
模型单元为三维实体单元,每个单元定义了10个节点,每个节点有三个自由度。本文只考虑玻璃板的应力,因此在处理不同材料的接触面时,支承头与垫层采用粘结方式,而考虑玻璃板与垫层间的接触。用柔体与柔体的面面接触单元进行模拟,垫层为接触面,采用conta174单元,玻璃板为目标面,单元为targe170。通过实常数和单元关键字来控制接触行为,接触算法采用程序默认的扩张的拉格朗日法,每运算一个荷载子步,系统自动调整接触刚度;为简化计算,接触表面采用no-separation方式,即一旦接触就不分开但允许有相对滑动,摩擦系数取为0.2;其余计算参数采用系统默认数值。在玻璃板的两侧面施加正对称约束,在连接件底部施加固定约束,在玻璃表面施加风荷载2.0kN/m2,不考虑连接件对玻璃板的预紧力作用。
(二)计算参数
本文主要分析了孔径、孔心边距、玻璃厚度、玻璃尺寸、金属支承头的尺寸(主要是金属压板的尺寸)、垫层的厚度及物理力学性能等因素对孔边应力的影响。
支承头的尺寸参数见图1,垫层的几何尺寸由玻璃板和连接件的尺寸相应确定。
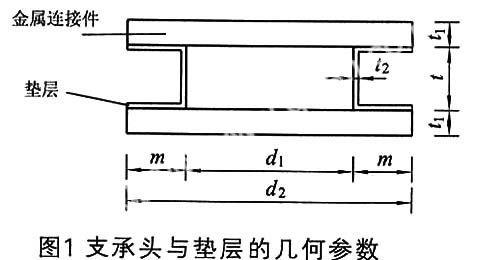
模型中各部分的基本参数如下:玻璃板:尺寸a×b=2.0×2.0m,厚度t=10mm,孔径d=36mm,孔心边距dis=120mm,弹性模量E=0.72×105N/m2泊松比v=0.2;支承头:金属压板厚度t1=5mm,压板直径d2=50mm,弹性模量E=2.06×105N/mm2,泊松比v=0.3;垫层:厚度t2=2mm,弹性模量E=0.10×105N/mm2,泊松比v=0.4。以上述数据为基本,通过某些参数的变化来研究其对孔边应力的影响。
三、计算结果及分析
由于玻璃为脆性材料,一般采用最大主应力原则来判断玻璃材料的破坏状态。因此,在本文分析中,只察看玻璃板的最大主应力。下述的大量算例表明,远离孔的区域主应力很小,而孔附近的应力集中现象很明显。
(一)孔径和玻璃厚度的影响
图2是在相同的孔心边距情况下,孔边应力随孔径和玻璃厚度的变化情况。分析结果表明,应力集中程度随孔径的增大而减缓;当玻璃厚度超过12mm后,孔径对应力集中的影响不明显。从图中可以看出,玻璃厚度不宜小于10mm,孔径宜取大,但孔径的增大意味着连接件的增大,这必然会带来成本的上升。

(二)孔心边距(孔边距)的影响
图3是在不同的玻璃尺寸情况下,孔边应力随孔心边距的变化情况。从图中可以看出,随着孔心边距的增大,孔边应力逐渐减小,且变化梯度也在减小,当孔心边距大于100mm时,可以认为孔边应力减缓的趋势不太明显;随着玻璃尺寸的增大,孔边应力有明显的增大。
图4为不同的孔径及相应的孔边距引起的孔边应力与玻璃边缘应力。孔边距对孔边应力的影响可通过孔心边距的影响来体现,但孔边距的大小对靠近孔的玻璃边缘的应力影响较大,见图4(b)。并且由于外围玻璃板的反翘作用,增大孔边距对玻璃板的大面应力是有利的。在实际工程中,由于玻璃自重会产生对玻璃孔的挤压作用,若孔边距较小,在玻璃自重等剪切荷载作用下,虽然玻璃板被剪断的可能性不大,但应力集中肯定会加剧。有资料要求孔边距不小于70mm[2],从分析中看,是比较合理的。
笔者建议,在使用固定支承头时,玻璃尺寸不应太大,宜控制在2m以下,同时孔心边距宜不小于100mm。

(三)玻璃长宽比的影响

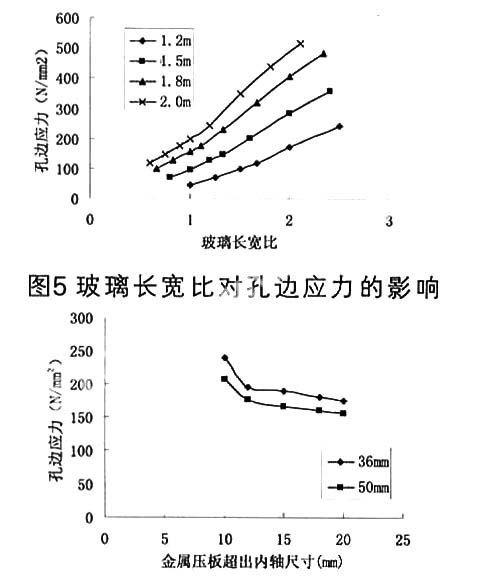
图5为不同玻璃宽度和长宽比对孔边应力的影响,玻璃板的长宽比对最大主应力影响较大,基本上呈线性关系,随着玻璃宽度的增大,其影响增大。一般来讲,玻璃的长宽比不宜超过2。
(四)金属压板尺寸的影响
如图6,随着压板尺寸的增大,孔边应力逐渐较小,最大主应力发生的位置由玻璃孔边缘变化到与压板边缘接触的玻璃板面,但当压板尺寸超过一定尺寸后,加大压板尺寸并不能明显减少孔边的应力集中。压板半径一般要比支承头内轴半径大12~15mm。
(五)垫层厚度及弹性模量的影响
目前垫层材料以塑料材料为主,拉伸模量在200~35000N/mm2范围内,泊松比在0.38~0.49之间,常用垫层厚度为1.2~9mm[6]。
垫层厚度对孔边应力的影响见图7。垫层厚度取1mm左右时,孔边应力出现最小值,垫层厚度小于1mm,孔边应力有急剧的增大。当垫层厚度大于1mm时,从(a)中发现,随着垫层厚度的增大,孔边应力增大,这是因为在金属压板尺寸相同的情况下,垫层厚度的增大意味着压板超出玻璃孔边的尺寸减小,从而导致应力的增大;(b)图中,在保证金属压板超出玻璃孔边的尺寸不变的情况下,垫层厚度对孔边应力的影响很小。因此,垫层不宜取得太厚,但考虑建筑和施工方便等因素,垫层厚度也不能太小,一般在2mm左右。

垫层弹性模量对孔边应力的影响见图8。弹性模量在1000~3000 N/mm2之间时,孔边应力取到最小值,因此实际应用中应在此范围取值;随后随着弹性模量的增大和减小,孔边应力都在增加,但总体来说,工程应用中应选用弹性模量较小的垫层材料。
四、小结
点式玻璃板受力弯曲后边缘翘曲,板面转动,固定式支承头不能随之转动,使玻璃板受到较强的约束,应力集中程度严重。通过以上的分析,可得出:
(一)对固定式支承头点式玻璃,孔边应力集中严重,一般都超过钢化玻璃的设计强度。在分析中没有考虑在形成玻璃孔过程中产生的微裂纹等缺陷,因此实际情况可能更严重。
(二)玻璃板的尺寸及长宽比对玻璃板最大主应力影响较大,因此使用固定式支承头时,玻璃板尺寸不应太大,且长宽比不宜超过2。
(三)孔心边距、孔径和压板尺寸的增大都能有效地减缓孔边的应力集中,但相应的使支承构件的尺寸增大,经济性变差,因此要综合考虑,选取合适的尺寸。
(四)垫层的厚度及弹性模量对孔边的应力也有影响,但影响不大。
(五)本文的分析模型是浮头式支承头,对于沉头式支承头,由于支承头与玻璃板接触面积小,应力集中现象会更明显。
综上,由于固定式支承头导致玻璃受力不合理,因此它在工程中应用不多,主要应用在荷载效应较小和幕墙分格尺寸不太大的情况。实际上,固定式支承头是早期点式幕墙中应用较多的支承装置,随着对点式玻璃幕墙的了解,现在工程中大都采用活动式支承头,相对于固定式支承头,其构造、生产并不复杂,而受力性能却优越的多,因此活动式支承头必将完全取代固定式支承头。从这种意义上讲,相应规范可以不再将固定式支承头列入点式玻璃幕墙所用的支承构件中。
本文虽然是以固定式支承头为例来分析点式玻璃板的应力集中情况,但影响玻璃孔边应力集中的因素及其中的某些结论对活动式支承头点式玻璃板也是适用的。
参考文献
[1]点支式玻璃幕墙工程技术规程 CECS 127:2001
[2]玻璃幕墙工程技术规程 JGJ 102-2003北京:中国建筑工业出版社2003
[3]杨威,王元清等。孔边应力状态对点式支承玻璃板承载性能的影响分析。建筑结构 2001,36(6)
[4]杨威,王元清等。玻璃建筑中带孔点式支承玻璃承载性能研究。工业建筑 2000,30(10)
[5]Andreas Klinkenberg. Untersuchungen zur statisch optimalen Halterposition bei punktge-stutzten Glastafeln. Stahlbau 1998(4)
