河床式电站大坝泄洪流场的三维数值模拟

杨京广，把多铎，林劲松，童 星

（西北农林科技大学水利与建筑工程学院，陕西杨凌 712100）

河床式电站大坝泄洪流场的三维数值模拟

杨京广，把多铎，林劲松，童 星

（西北农林科技大学水利与建筑工程学院，陕西杨凌 712100）

在1∶100水工模型试验的基础上，应用k-ε紊流数值模型，采用VOF方法，对低水头大流量河床式电站大坝泄洪流场进行了三维数值模拟。将计算得出的各工况下泄洪闸闸室及下游流场的流态，水面线，闸室内流速、压力分布等水力特性值与试验数据对比，发现计算值与试验值基本吻合。说明所选择的紊流数学模型，建立基本控制方程以及求解数学模型的离散方法是比较可靠的，可以为工程设计提供参考。

VOF；k-ε；紊流模型；河床式电站

随着计算技术的日趋成熟和计算机性能的不断提高，越来越多的水利工作者将计算机这一工具应用于水利工程的数值计算。数值模拟花费少、速度快、信息完整等优点逐步显示出来，并逐渐被工程界所接受，成为物理模型试验的重要补充手段。

关于数值模拟在水利工程中的应用，国内外学者已经做了不少工作。如李玲［1］等人对溢洪道出口扭曲型挑坎水流进行数值模拟；张盾［2］等人对渥奇面掺气挑坎位置进行二维数值模拟研究；沙海飞［3］等人采用三维紊流模型，对泄洪洞整体进行了数值模拟；吕欣欣［4］采用紊流模型，对低水头大流量厂坝联合泄流消能流场进行了二维数值模拟研究。

1 工程概况

本文对黄河河口水电站［5］泄洪闸泄流进行了三维数值模拟研究。河口水电站是一座中型河床式水电站，枢纽建筑物从左至右依次由安装间坝段、厂房坝段、冲沙闸（2孔）、泄洪闸（5孔）、右岸挡水坝段及GIS开关站组成，具体布置如图1所示，泄洪闸体型如图2所示。

2 数值计算

2.1 数学模型的控制方程

连续方程：

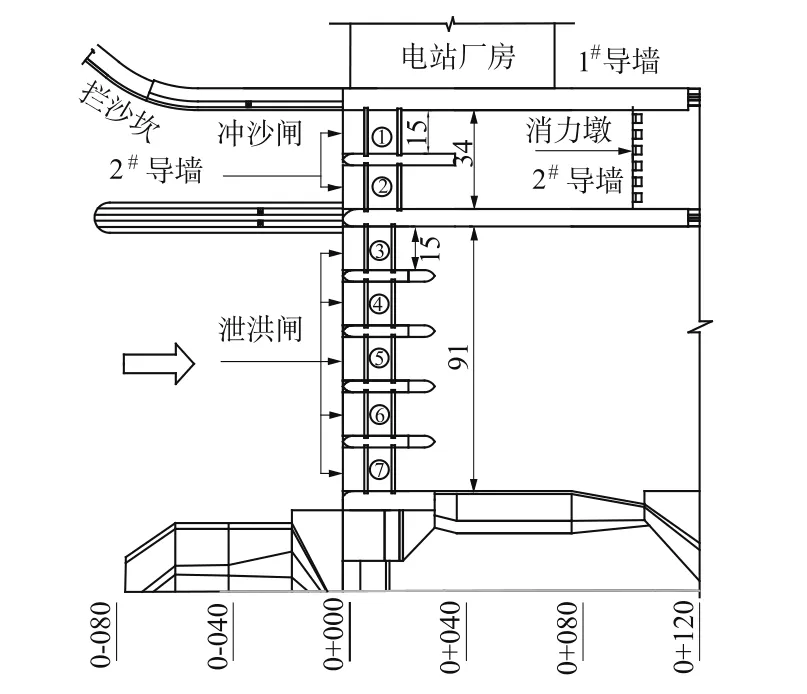
图1 枢纽布置图（单位：m）Fig.1 General layout of Hekou Hydropower Station on the Yellow River（unit inm）

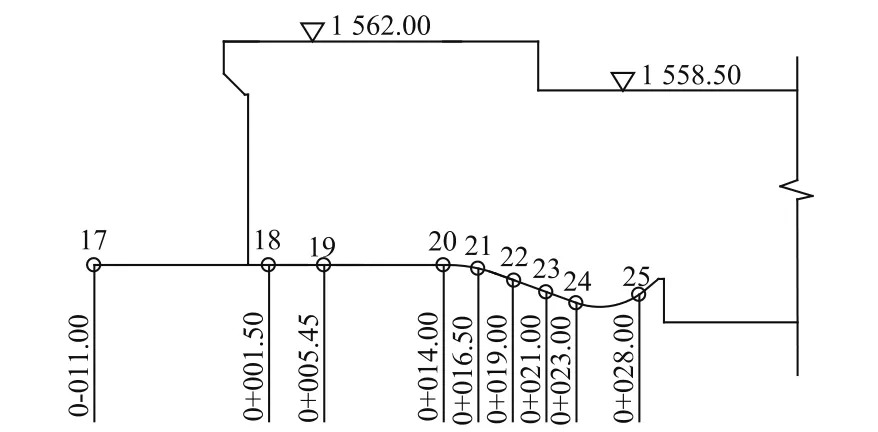
图2 泄洪闸纵剖面及测压孔布设图（单位：m）Fig.2 Profile of release sluice and pressuremeasurement holes arrangement（unit inm）

动量方程：

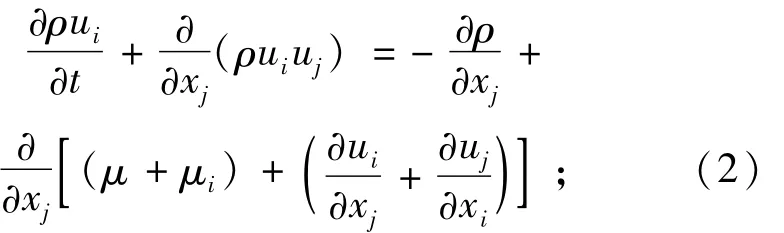
k方程：

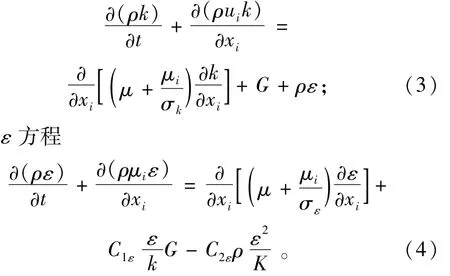
式中：ui为xi方向的速度分量，i，j＝1，2，3；ρ为体积分数的平均密度；p为修正压力值；μ是体积分数平2均的分子黏性系数，u取值为0.09；σk和σε为k和ε的紊流普朗特数，σk＝1.0，σε＝1.33；C1ε和C2ε为ε程常数，取C1ε＝1.44，C2ε＝1.92；G由平均速度梯度引起的紊动能产生项，

式中的ρ和μ不是常数，而是体积分数的函数，计算公式如式（6）和式（7）所示，

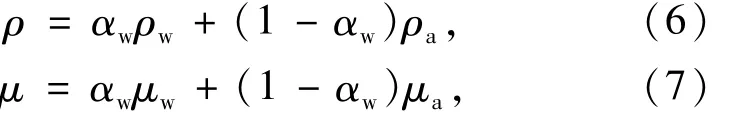
式中：αw为水的体积分数；ρw和ρa分别为水和气的密度；μw和μa分别是水和气的黏性系数。

2.2 数值求解

采用有限体积法（Finite Volume Method）进行数值求解。首先将计算区域划分网格，使每个网格点周围有一个互不重复的控制体积，将控制方程对每一个控制体积积分，再把积分方程线性化，得到各未知变量的代数方程组，求解这些方程组便可以求出各未知变量。各控制方程的通用形式如式（8）所示。

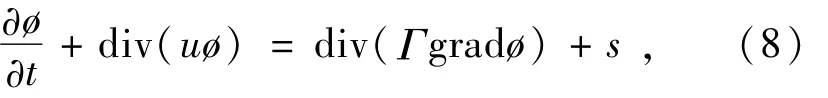
式中：ø为通用变量，可以代表u，v，w，k和ε等变量；Γ为广义扩散系数；s为广义源项。控制方程中，ø和Γ的具体形式如表1所示。

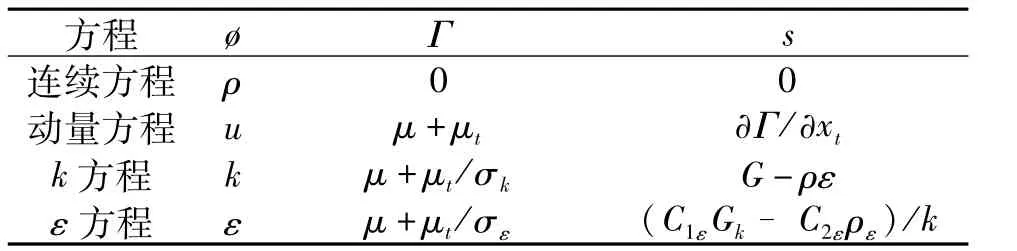
表1 各输运方程中ø，Γ和s的具体形式Table1 The concrete forms ofø，Γand s used in transportation equation

对方程（8）在任意控制体积作体积分，利用高斯定理将体积分化为面积积分。如果令F（ø）＝ρøu-Γøgradø，则有限体积法的基本方程可以写为式（9）形式。

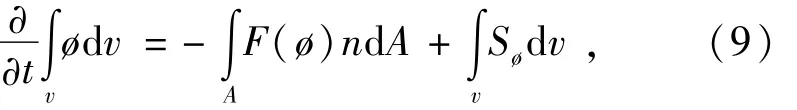
式中：F（ø）n为法向数值通量；A为表面矢量。

在一个给定的控制体中对方程进行离散，得

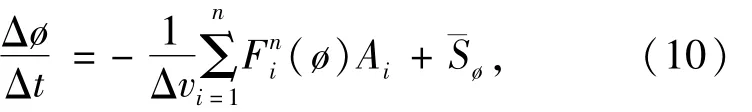
式中：Δv为单元体积；n为围成单元面的个数；Ai为第i个单元面的面积；¯Sø为单元的源相平均值。

3 网格划分及计算条件

3.1 网格划分

本文对泄洪闸进行了数值计算，模拟的区域包括5孔泄洪闸，模拟上游库区30 m和下游河床段70 m，泄洪闸单宽15 m，高16 m。由于模拟的计算区域较大，在某些部位不可避免出现体型不规则，因此，在进行网格划分时采用结构化网格与非结构网格相结合的方法。划分的网格单元数约为37万。

3.2 边界条件

进口边界：进口采用水流速进口，对于某一指定工况下，紊动能k和耗散率ε可由下列经验公式得出。

式中L为紊流特征长度。

出口边界：出口边界条件根据下游流量水位关系确定。

壁面条件：采用Launder&Spalding的壁面函数法。

自由水面：采用VOF方法追踪自由水面。VOF方法认为在每个单元中，水和气的体积分数αw与αa之和为1，水的体积分数为αw，气的体积分数为αa，当αw＝1时，表示该单元内全部是水；当αw＝0时，表示该单元全被气充满；当0＜αw＜1时，表明该单元部分是水，部分是气，有水气交界面。

4 计算结果及分析

按照上述计算条件，对泄洪闸各工况进行了流场计算，由于篇幅限制，只对大流量30年一遇洪水（6 170 m3／s）举例说明。当遭遇30年一遇洪水时，5孔泄洪闸全开，2孔冲沙闸局开7.2 m，库水位为1 558.00 m，下游水位为1 556.08 m，泄洪闸过流量为4 699 m3／s，2孔冲沙闸过流量为1 471 m3／s。计算分别得出了泄洪闸内水面线、压力及流速分布。图3为控制体积内气所占比例的数值计算结果。从图中可以比较清晰地看见水和大气的分界线。

图3 控制体积中气的体积分数Fig.3 Air fraction in control volume

4.1 水面流态

从模型试验可以看出，当泄洪闸遭遇30年一遇洪水（6 170 m3／s）时，水闸上游水面较为平稳，左右各孔进流均匀，无横向水面跌落、回流等，且各闸室内水流对称，左右侧水面线高度基本相等，有弱水跃发生。图4为泄洪闸实测水面线与计算水面线比较。从计算曲线可以看出，水面线较为平稳，在闸室内有弱水跃，与试验观察基本一致。由图还可以看出水流从水库流出，在到达堰顶之前出现水面跌落，这是因为进入堰顶的水流，受到堰顶垂直方向的约束，过水断面减小，流速加大。由于动能加大，势能必然减小，再加上水流进入堰顶时产生局部能量损失，所以进口处形成水面跌落，这是符合宽顶堰出流的特点。

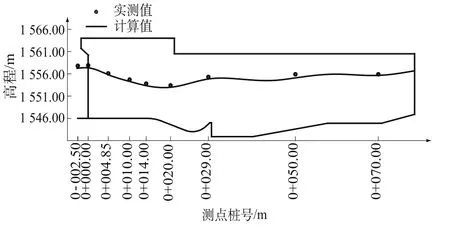
图4 水面线实测值与计算值对比Fig.4 Calculated water surface line compared with themeasured one

笔者还对控制断面处水面高程实测值和计算值作了比较，从比较结果来看，实测值与计算值的差值在0.18～0.55 m之间，大致相差1.3%～5.4%，两者基本吻合。引起误差的原因可能有2点，①试验过程中的测量误差；②网格划分不够细，会引起计算结果偏离真实值。

4.2 压强分布

计算了泄洪闸内沿底板中心线时均压强的分布，泄洪闸内共安装了9个测压孔，其具体分布位置如图2所示。图5是流量为6 170 m3／s时，泄洪闸纵剖面计算得出的压强分布等值线图，从图中可以看出，闸室内压强分布比较均匀。

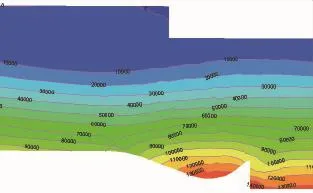
图5 泄洪闸内压强分布等值线Fig.5 Pressure distribution contour lines in release sluice

图6 为泄洪闸底板中线沿程压强分布的计算值与实测值之间的对比。由图可见压强的计算值与实测值在分布趋势和大小上均吻合得比较好，在模型体型突变的位置，压强变化较大。压强分布符合常规宽顶堰和反弧挑坎的压强分布规律。可以看出，自反弧段中心位置至鼻坎出口处，压强呈逐渐减小的趋势；堰面上没有出现负压，在体型突变的位置压强较小。下游压强分布比较均匀，没有突变的位置。说明泄洪闸体型设计是比较合理的。

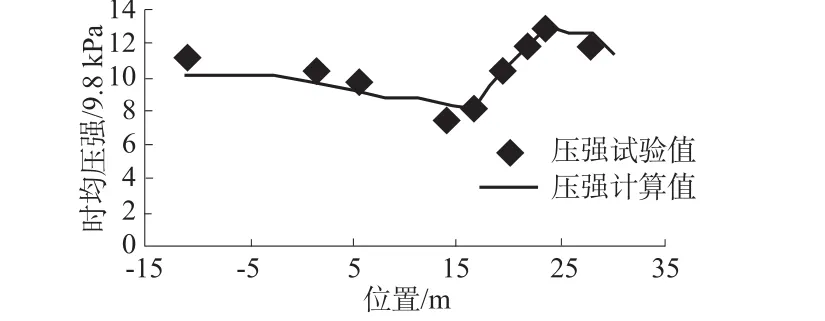
图6 泄洪闸底板压强计算值与实测值对比Fig.6 Calculated pressure values compared with measured data on release sluice floor

4.3 流速分布

图7、图8为泄洪闸内坝轴线线处、坝下0+10 m、0+20 m以及0+26 m处流速沿水深方向，计算值与实测值之间的对比。从图中可以看出，计算值与实测值在大小和变化趋势上基本一致，速度平均值相差不大，大致相差在0.01～0.17 m／s的范围。从图4水面线形状可以看出，闸室内弱水跃跃前位置在坝下0+20 m左右，所以在该处出现流速最大，计算得出的表流速为9.81 m／s，试验得出为9.83 m／s；底流速计算值为9.07 m／s，试验测得为9.36 m／s。从以上对比可以分析得出，数值计算得出的结果是非常可靠的。

图7 0+0m、0+10m处流速试验值与计算值Fig.7 Measured and calculated velocities at0+0m，0+10m

图8 0+20m、0+26m处流速试验值与计算值Fig.8 Measured and calculated velocities at0+20m，0+26m

5 结 论

（1）河口水电站设计的枢纽整体布置是合理的，泄水建筑物位于主河槽上，泄流顺畅，泄洪闸进口水流对称，闸室内水流平稳，无脱壁、立面漩涡等不利流态，出闸水流顺直，两岸无明显回流。

（2）泄洪闸内水面线、流速及压强分布合理，说明枢纽建筑物体型设计是合理的；泄水建筑物及上、下游河道流态平顺。

（3）应用k-ε两方程模型、VOF法对低水头大流量河床式水电站泄洪流场进行了三维数值模拟，计算得出了泄洪闸各工况下的水面线、闸室内压强及流速分布。将模拟结果用试验资料进行了验证，发现该模型可以较精确地模拟泄洪闸内部过流的各项水力要素。应用该数学模拟方法，可以为设计工作者提供第一手快捷、准确的成果信息。

（4）应用成果信息，使水工设计提高效率和节省费用，并为物理模型试验提供前期预测和指导。

［1］ 李 玲，陈永灿，李永红.溢洪道出口扭曲型挑坎水流的数值模拟［J］.水力发电学报，2007，26（2）：79-82.

［2］ 张 盾，刘韩生.渥奇面上掺气挑坎位置的试验与数值计算分析［J］.山东大学学报，2008，38（2）：101-105.

［3］ 沙海飞，吴时强，陈振文.泄洪洞整体三维数值模拟［J］.水科学进展，2006，17（4）：507-511.

［4］ 吕欣欣，牛争鸣.低水头大流量厂坝联合泄洪消能流场的二维数值模拟［J］.西北水力发电，2007，23（2）：10-14.

［5］ 林劲松，刘韩生，许海军，等.黄河河口水电站可研阶段整体水工模型试验报告［R］.陕西杨凌：水利部西北水利科学研究所试验中心，2006.

（编辑：周晓雁）

Three-Dimensional Numerical Simulation on Flood Field of Riverbed Hydropower Station

YANG Jing-guang，BA Duo-duo，LIN Jing-song，TONG Xing
（College ofWater Resource and Architectural Engineering，Northwest A＆F University，Yangling 712100，China）

On the basis ofmodel test，a 3 D numerical simulation on the flow field of low waterhead and big discharge riverbed hydroelectric station wasmade by adopting k-εturbulencemodel and VOFmethod.The calculated flow pattern，water surface line，flow velocities，and the pressure distributions were compared with test results.The results show that the calculated results are in good agreement with the experimental data.It is proved that the turbulentmathematical model，the basic control equation and discrete method are reliable.The results can be used for the engineering design.

VOF；k-ε；turbulencemodel；riverbed hydroelectric station

TV135.2

A

1001-5485（2009）08-0028-04

2008-10-17；

2008-12-20

西北农林科技大学人才培养基金

杨京广（1982-），男，湖南湘乡人，硕士研究生，主要从事水工水力学方面研究。（电话）13720418202（电子信箱）yjg1022＠yahoo.cn。