在小学数学中渗透函数思想的有效途径

汤咏梅

《数学课程标准》的总体目标要求学生在掌握重要的数学知识的同时了解基本的数学思想方法，因此，在小学数学教学中向学生渗透一些函数思想，是培养学生分析、解决问题能力的重要途径，也为学生初中学习函数知识打下基础。

一、在知识与技能的学习中，渗透函数思想

1.在概念教学中渗透函数思想，能使学生理解概念，揭示其本质属性。

小学数学课本中的概念，因受学生知识、年龄、认识水平等因素的制约，大多数概念的引进都采用描述性方法，缺乏完整的内涵和外延。因此，教师在教学中要善于把握教材，善于运用函数思想，以便让学生能从数学思想方法的高度来认识和掌握概念。

如在正比例的教学中：一辆汽车在公路上行驶，行驶的时间和路程如下表：

通过教学让学生理解路程和时间是两种相关联的量，时间变化，路程也随着变化，当路程和对应时间的比值总是一定时，我们就说行驶的路程和时间成正比例。因此，概念的教学中，教师应尽可能从各方面借助各种教学手段，不断充实内涵，扩展外延，渗透数学思想方法，真正揭示概念的本质属性。

2.在解决问题的教学中渗透函数思想，培养学生解决问题的能力。

解决问题教学是小学数学教学中的重要组成内容和环节。通过解题训练，培养学生的思维，更重要的还可以培养学生的创造性思维，达到提高学生解决问题和创造性解决问题的能力。因此，教师更应抓住有利时机，精心巧妙地设计教学，突出和强化函数思想对解题的指导作用。

如：每边坐一人的方桌，2张拼起来可坐6人，3张、4张、5张…拼起来，各可坐多少人?(如下图)

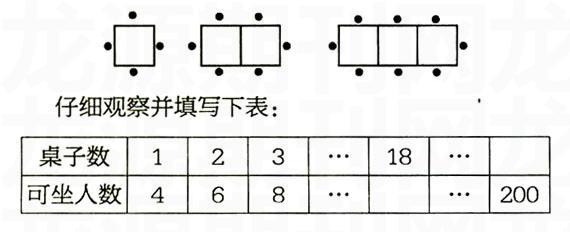
随着桌子数的变化，可坐人数也随之变化。而且是有一定规律的变化。教师在这里要注意引导学生通过观察表格，找出其中变化的规律，并运用函数思想来解决问题。

二、在学习的过程与方法中，渗透函数思想

1.在探索知识的发生、形成过程中渗透函数思想，能使学生运用数学思想和方法进行类推。

例如，在推导圆锥体积公式时，首先回忆平面图形中三角形面积公式的推导过程，明确转化方法是两个完全一样的三角形拼成一个平行四边形，这为圆锥体积中也是由3个等底等高的圆锥体积拼成一个圆柱体积提供内在的类比逻辑和化归的思路。然后引导学生观察等底等高的空心圆柱和圆锥，由直觉猜想两者体积之间的关系。如下图：

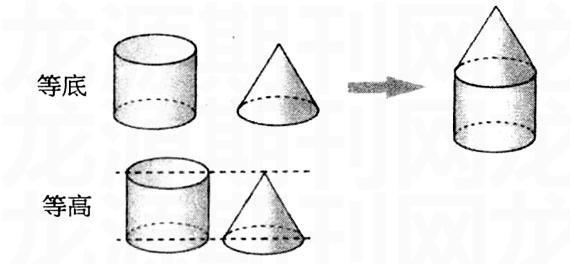
最后引导学生进行实验设计，形成实验思想。像这样有思想深度的课，给学生留下了长久的思想激动和知识的深刻理解，方法也渗透于无形之中。

2.在解决实际问题中领悟函数思想。

加强数学应用意识，鼓励学生运用数学知识去分析解决生活中的实际问题，引导学生抽象、概括，建立数学模型，探求问题解决的方法，使学生在把实际问题抽象成数学问题的过程中，进一步领悟数学中的定义、概念、定理、公式等。

如：用60元去购买笔记本，笔记本的单价和可以购买的数量如下表：

引导学生观察：笔记本的单价变化，购买的数量也随着变化，但可以看出总价是不变的。因此，可以用式子表示上面几个量之间的关系：单价×数量=总价(一定)。单价和数量是两种相关联的量，单价变化，数量也随着变化。当单价和对应数量的积总是一定时，我们就说笔记本的单价和购买的数量成反比例，笔记本的单价和购买的数量是成反比例的量。这样，学生在解决实际问题中不仅掌握了反比例的概念，而且从中领悟到了数学中的函数思想。

虽然，在小学阶段没有出现“函数”这一概念，但在整个小学阶段的数学学习中，无不渗透函数的思想。可以这样说，凡是有“变化”的地方就蕴含着函数思想。函数数学思想相对于教材而言，是隐性工程，它是学生获得数学知识、发展思维能力的动力和工具，是我们进行教学设计和教材重组的指导思想。对学生进行函数数学思想的渗透，不是一朝一夕就能见到学生数学能力提高的，而是有一个过程，必须经过循序渐进和反复训练，才能使学生真正地有所领悟。