几种矩阵逆的连续性

吴池业,黄廷祝

(电子科技大学应用数学学院,四川成都 610054)

几种矩阵逆的连续性

吴池业,黄廷祝

(电子科技大学应用数学学院,四川成都 610054)

非奇异矩阵的逆是矩阵元素的连续函数.学者们也对矩阵广义逆的连续性有所研究.本文应用矩阵分裂和两个矩阵之和的逆的展开式,给出了一般非奇异矩阵,M-矩阵和H-矩阵的逆的连续性．当一些合理的条件满足时,这几种矩阵的逆是连续的.

连续性;矩阵逆;M-矩阵;H-矩阵;广义逆

1 引言

对大多数的数值分析者来说,矩阵逆是不合常理的.不但是因为矩阵逆的工作量接近于一般矩阵乘法工作量的三倍,而且不稳定[1].另外,很少矩阵逆是连续的.当A是非奇异方阵时, Moore-Penrose广义逆等同于A的一般矩阵逆A−1.众所周知[2],对于使得‖I‖=1任意矩阵范数‖·‖,如果‖E‖＜1,则

的充分条件是对于充分大的n,En的行和列位于A的行空间和列空间.广义逆连续性的充要条件是Stewart[4]给出的.他给出了在(2)和(3)的条件下(4)成立的充要条件是对于充分大的n都有rank(A+En)=rank(A).Campbell和Meyer[5]也提供了M-P和Drazin广义逆的连续性性质.

首先,我们提供两个本文所需的定义

其中P是非负的,ρ(P)是P的谱半径且当s＞ρ(P)时,A称为M-矩阵.

M-矩阵有两个主要特征:

(ii)A是稳定的.

n阶矩阵A称为H-矩阵,如果A的比较矩阵µ(A)=(αij)是M-矩阵,其中αii=|aii|且αij= −|aij|(i/=j).

M-矩阵和H-矩阵在数值分析,数学物理,控制论和经济学中有非常重要的应用[68].本文给出了关于一般非奇异矩阵,M-矩阵和H-矩阵逆的连续性的一些结论.明显地,本文的条件比文[9]中的条件简单.

全文中,对A=(aij)矩阵|A|被定义成|A|=(|aij|).

2 一般非奇异矩阵逆的连续性

3 M-矩阵逆的连续性

本节我们给出当满足一些特殊条件时,M-矩阵逆的连续性.

定理2若给M-矩阵A一个扰动△A,|△A|≤ε|A|,ε是充分小的正数且A+△A非奇.则

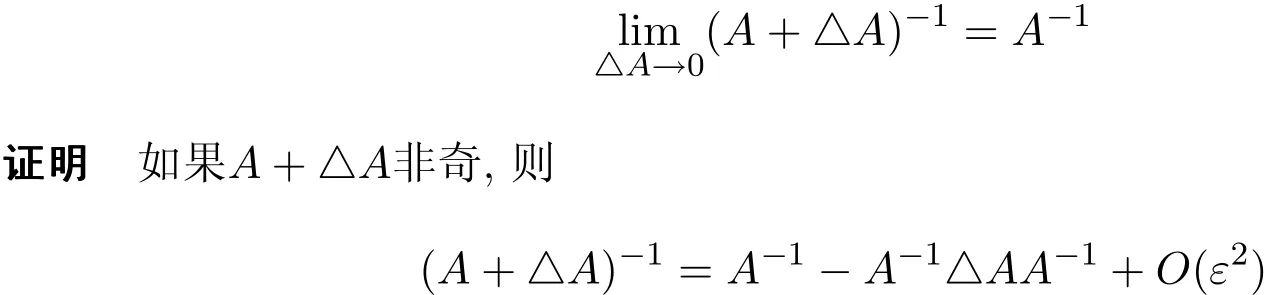
故

定理2的条件明显比引理2的条件要简单.此外,当ε充分靠近于0时,ερ(A−1|A|)＜1总是可以达到的.故在定理2的条件下中,我们将其省略.

4 H-矩阵逆的连续性

本节我们给出当满足一些特殊条件时,H-矩阵逆的连续性.

定理3若给不可约H-矩阵A一个扰动△A使得B=A+△A,其中B是非奇异的且△A= diag(ε1,ε2,…,εn)≥0.则

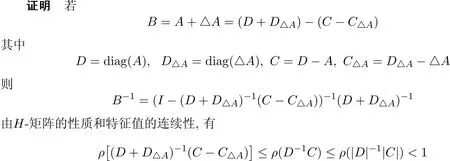
接下来的证明类似于定理3的证明,此略.

[1]Higham N J.Accuracy and Numerical Algorithm[M].Philadephia:SIAM,1996.

[2]Wilkinson J H.Rounding Error in Algebraic Process[M].Englewood Cliff,NJ:Prentice-Hall,1963.

[3]Ben-Israel A,Charnes A.On error bounds for the generalized inverse[J].SIAM J.Numer.Anal.,1966, 3(4):585-592.

[4]Stewart G W.On the continuity of the generalized inverse[J].SIAM J.Appl.Math.,1969,17(1):33-45.

[5]Campbell S L.On the continuity properties of Moore-Penrose and Drazin generalized inverse[J].Ibid,1977, 18(1):53-57.

[6]Windisch G.M-matrices in Numerical analysis[M].Leipzig:Teubner-Texte zur Mathematik,1989.

[7]Takayama A.Mathematical Economics[M].Cambridge:Cambridge University Press,1988.

[8]Horn R A,Johnson C R.Topics in Matrix Analysis[M].Cambridge:Cambridge University Press,1985.

[9]Wei Yimin,Cao Yanhua,Xiang Hua.A note on the componentwise perturbation bounds of matrix inverse and linear systems[J].Appl.Math.Comp.,2005,169(2):1221-1236.

On the continuity of several kinds of matrices inverse

WU Chi-ye,HUANG Ting-zhu
(School of Applied Mathematics,University of Electronic Science and Technology of China, Chengdu610054,China)

The inverse of a nonsingular matrix is a continuous function of the elements of the matrix.The continuity of the generalized inverse A+of a matrix A was also investigated by scholars.In this paper,applying matrices splitting and the expansion of inverse of sum of two matrices,the continuity of matrices inverse,such as general nonsingular matrices,M-matrices and H-matrices,respectively,is provided.Inverses of these matrices are continuous when some reasonable conditions are satisfied.

continuity,matrix inverse,M-matrix,H-matrix,generalized inverse

O241.6

A

1008-5513(2009)03-0481-05

2007-04-02.

国家自然科学基金(10771030),教育部科学技术研究重点项目(107098),四川省应用基础研究项目(2008JY0052),高等学校博士点专项科研基金(20070614001),电子科技大学“中青年学术带头人+创新团队”项目.

吴池业(1978-),博士生,研究方向：数值算法的稳定性和精确性.

2000MSC:65F10