关于Smarandache-Type可乘函数的方程

张小蹦,田清

(1.西安邮电学院应用数理系,陕西西安 710121;2.西北大学数学系,陕西西安 710127)

关于Smarandache-Type可乘函数的方程

张小蹦1,2,田清2

(1.西安邮电学院应用数理系,陕西西安 710121;2.西北大学数学系,陕西西安 710127)

研究了一类包含Smarandache-Type可乘函数Fk(n)与Gk(n)的无穷级数及其算术性质,并利用初等方法及欧拉积公式得到了该级数的两个有趣的恒等式,从而推广了关于Smarandache-Type可乘函数的算术性质.

Smarandache-Type可乘函数;无穷级数;恒等式

1 引言

此外，对于任意的正整数n,Smarandache k次幂剩余ak(n)是指满足nak(n)为一个完全k次幂的最小正整数.即

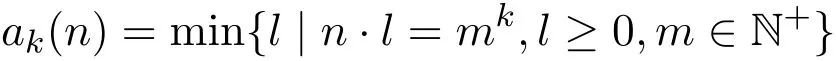
从ak(n)的定义中,我们发现ak(n)仍是一个可乘函数.设A表示满足方程Sk(n)=ak(n)的所有正整数n的集合.即A={n∈N,Sk(n)=ak(n)}.目前,有许多关于Smarandache ceil函

其中ζ(s)表示Riemann-zeta函数.

定理2设k是一个大于等于2的正整数.则对于任意的实数s＞1,有

2 定理的证明

我们直接给出定理的证明.首先,定义算术函数B(n)为

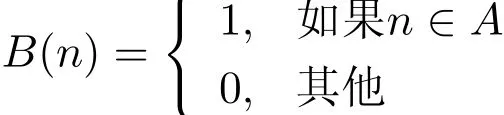
利用同样的方法,也可以得到

于是完成了定理的证明.

[1]Smarandache F.Only Problems,Not Solutions[M].Chicago:Xiquan Publishing House,1993.

[2]Ibstedt Surfinig.On the Ocean of Number-a few Smarandache Notions and Similar Topics[M].New Mexico: Erthus University Press,1996.

[3]Sabin Tabirca,Tatiana Tabirca.Some new results concerning the Samarandache ceil function[J].Smarandache notions Journal,2002,13:30-36.

[4]Apostol T M.Introduction to Analytic Number Theory[M].New York:Springer-Verlag,1976.

[5]易媛,亢小玉.关于Smarandache问题研究[M].USA:High American Press,2006.

[6]苟素.关于Smarandache ceil函数的一个方程[J].纯粹数学与应用数学,2006,22(1):48-50.

Equations on the Smarandache-Type multiplicative function

ZHANG Xiao-beng1,2,TIAN Qing2
(1.Department of Applied Mathematics and Physics,Xi’an University of Post and Telecommunications, Xi’an710121,China;2.Department of Mathematics,Northwest University,Xi’an710127,China)

The main purpose of this paper is using the elementary method and Euler product formula to study the properties of the infinity series involving the Smarandache-Type function,and obtain its two interesting identities.This generalized the properties of Smarandache-Type function.

Smarandache-Type multiplicative function,infinity series,identity

O156.4

A

1008-5513(2009)03-0478-03

2008-09-14.

陕西省教育厅专项科研计划项目(08JK437),西安邮电学院中青年科研基金(105-0449).

张小蹦(1978-),助教,研究方向：数论及其应用.

2000MSC:11B83