关于SSSP(n)和SISP(n)的均值

苟素

(西安邮电学院应用数理系,陕西西安 710121)

关于SSSP(n)和SISP(n)的均值

苟素

(西安邮电学院应用数理系,陕西西安 710121)

研究了Smarandache最小平方数列和Smarandache最大平方数列的均值性质,并用初等方法得到了关于这两个数列均值的渐近公式.

Smarandache最小平方数；Smarandache最大平方数；均值；渐近公式

1 引言及结论

对任意非负整数n,我们用SSSP(n)表示n的Smarandache最小平方数,即就是大于或等于n的最小完全平方数.例如该数列的前几项为:0,1,4,4,4,9,9,9,9,9,16,16,16,16,16, 16,16,25,….用SISP(n)表示n的Smarandache最大平方数,即就是不超过n的最大完全平方数.这个数列的前几项为:0,1,1,1,4,4,4,4,4,9,9,9,9,9,9,9,16,16,16,16,16,16, 16,16,16,25,….令

由以上定理立刻得到下面的:

推论1对任意正整数n,有渐近式及极限式

推论2对任意正整数n,有渐近式及极限式

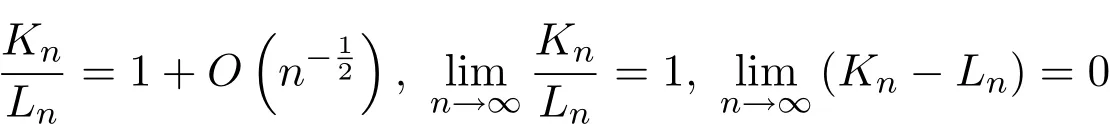
2 定理的证明

于是完成了定理中第一个渐近公式的证明.

同理,对任意实数x＞2,显然存在唯一的正整数M使得:M2≤x＜(M+1)2,于是有

由以上两个式子立刻得到

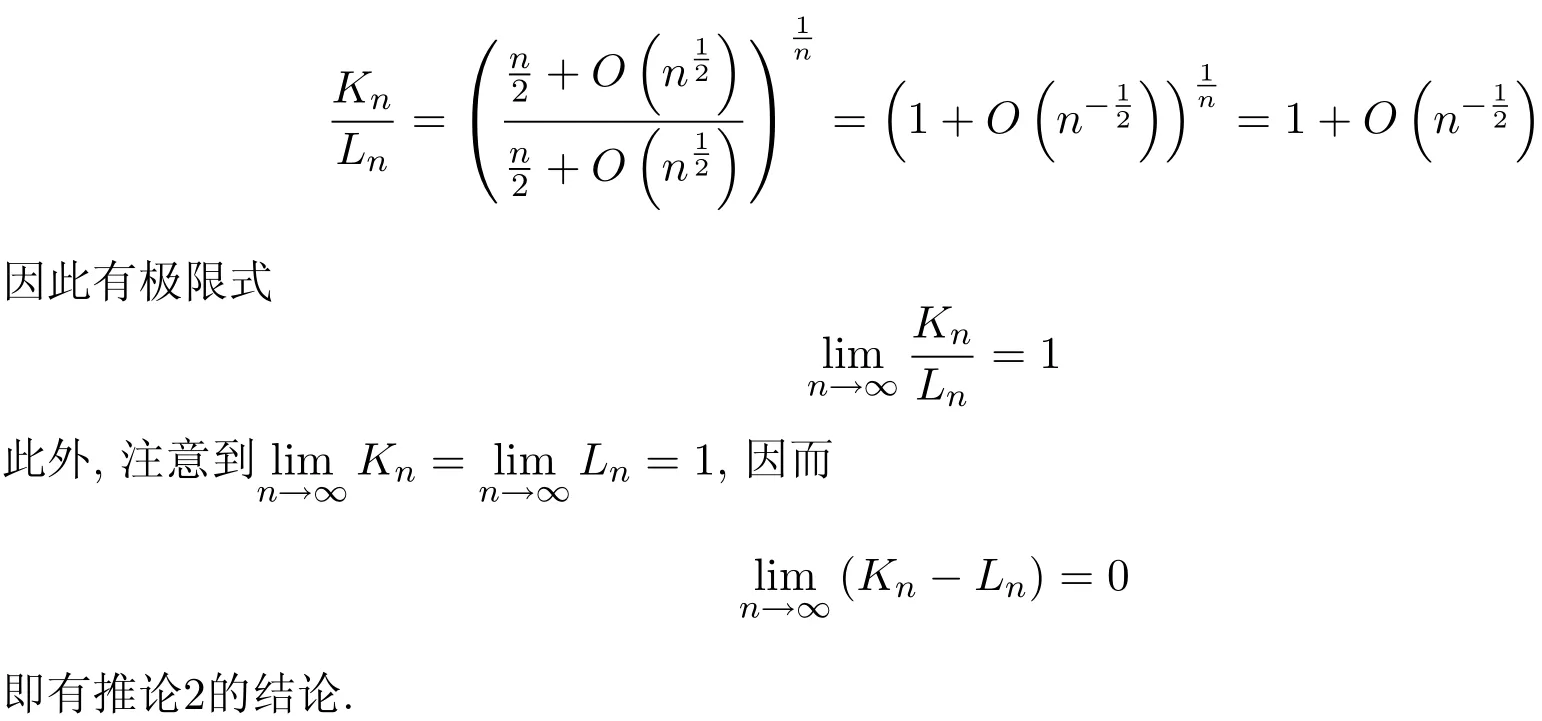
[1]Smarandache F.Only Problems,Not Solutions[M].Chicago:Xiquan Publishing House,1993.

[2]杜凤英.关于Smarandache函数S(n)的一个猜想[J].纯粹数学与应用数学,2007,23(2):205-208.

[3]沈虹.一个新的数论函数及其它的值分布[J].纯粹数学与应用数学,2007,23(2):235-238.

[4]Kenichiro Kashihara,Comments and Topics on Smarandache Notions and Problems[M],USA:Erhus University Press,1996.

[5]Apostol T M.Introduction to Analytical Number Theory[M].New York:Spring-Verlag,1976.

On the mean values of SSSP(n)and SISP(n)

GOU Su
(Department of Applied Mathematics and Physics,Xi’an Institute of Posts and Telecommunications, Xi’an710069,China)

For any positive integer n,the Smarandache superior square part SSSP(n)is the smallest square greater than or equal to n,the Smarandache inferior square part SISP(n)is the largest square less than or equal to n.The main purpose of this paper is using the elementary and analytic methods to study the arithmetical properties of these two sequences,and give two interesting mean value formulas for them.

Smarandache superior square part,Smarandache inferior square part,mean value,asymptotic formula

O156.4

A

1008-5513(2009)03-0431-04

2007-09-09.

国家自然科学基金(10671155),陕西省教育厅科研专项基金(08JK433).

苟素(1972-),副教授,研究方向：基础数学.

2000MSC:11B83