关于位数函数高次均值的计算
2009-07-05李海龙周军
李海龙,周军
(渭南师范学院数学与应用数学研究所,陕西渭南 714000)
关于位数函数高次均值的计算
李海龙,周军
(渭南师范学院数学与应用数学研究所,陕西渭南 714000)
针对1993年美国数论专家Smarandache提出了初等数论及集合论中的105个未解决的问题中的5个关于自然数列的性质问题,就自然数列的位数函数问题进行了研究,给出了在一个正整数的n进制表示中的位数函数定义,采用了归纳、猜想的方法得出了位数函数a(m,n)的高次均值的精确计算公式.
n进制;位数函数;均值
1 引言及结论
在文[1]中美国数论专家Smarandache提出了初等数论及集合论中105个未解决的问题让大家研究,其中有五个问题是关于自然数列的性质问题.文[2-4]给出了在一个正整数的n进制表示中数字之和函数以及它的一次、二次、三次均值的精确计算公式,文[3]主要研究数字之积函数的均值,文[5]给出了位数函数三次均值的计算公式.本文主要用了归纳、猜想的方法研究自然数列的位数函数,得出了在一个正整数n进制表示中的位数函数a(m,n)均值Ar(m,n),(r=1,2,3,···)的精确计算公式,并给出了证明.

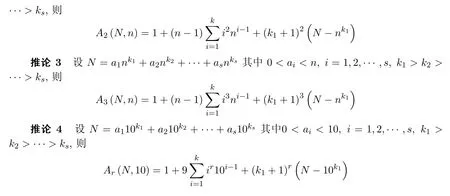
2 引理及其证明


3 定理的证明

参考文献
[1]Smarandche Florentin.Only Problems,Not Solutions![M].Chicago:Xiquan Publishing House,1993.
[2]李海龙,杨倩丽.关于n进制及其有关计数函数[J].纯粹数学与应用数学,2002,18(3):13-15.
[3]杨倩丽,李海龙.关于n进制中数字之和函数均值的计算[J].西北大学学报,2002,32(4):361-362.
[4]李海龙,杨倩丽.n进制中非零数字之积函数的均值公式[J].数学的实践与认识,2002,32(4):683-686.
[5]杨倩丽,仇英利,李海龙.关于位数函数三次均值的计算[J/OL].西北大学学报:自然科学网络版,2006,4(4):0218 [2006-07-10].http://jonline.nwu.edu.cn/wenzhang/206171.pdf.
On high power mean values computations of the location number function
LI Hai-long,ZHOU Jun
(Institute of Mathematics and Applied Mathematics,Weinan Teachers University, Weinan714000,China)
This article was inferred to 105 unsolution questions in primary theory of numbers and set theory which were proposed by American theory of numbers expert Smarandache in 1993 about the nature question of natural sequence,conducted the figure function question of the natural sequence.It was produced n the figure function definition in a positive integer in the system expression,and has used induction suspected methods then has obtained two direct the principle which was related to,also using these directed the principle to obtain Figure function a(m,n);High power mean values as mean as the precise formula on.
base n,function of the location number,average value
O156.4
A
1008-5513(2009)04-0770-04
2007-10-10.
陕西省自然科学基金(SJ08A22).
李海龙(1963-),教授,研究方向:数论.
2000MSC:11B83
