半参数回归模型独立情形的分离法估计
2009-07-05陈乃辉
陈乃辉
(中央财经大学应用数学学院,北京 100081)
半参数回归模型独立情形的分离法估计
陈乃辉
(中央财经大学应用数学学院,北京 100081)
对半参数回归模型,用L2最佳逼近加矩估计的方法,推出其非参数部分的依L2与强相合联合收敛意义下的估计,及参数部分的强相合与相合渐近正态估计,并设计实行了一个模拟实验.
半参数回归模型;随机函数逼近;矩估计;相合渐近正态性
1 引言
上世纪八十年代由Engle等[1]提出了如下的半参数回归模型(以回归函数的形式表现)

对此国内外学者多有很好的研究[26],其中的思想方法,是采用两阶段的想法相继将半参数回归模型化为非参数回归模型与参数回归模型分别予以解决,于后一阶段一般运用最小二乘方法,而于前一阶段有各种不同的手法,如核估计法[2],最近邻估计法[3]与小波估计法[4,6]等.
本文研究半参数回归模型(1.1)在X与(Z1,···,Zd)相互独立的情形,采用分离方法对其估计,即将模型的非参数部分与参数部分的估计完全分开而互不干涉地进行,而后合为对半参数回归函数的L2收敛强相合估计.该文的其它特点有:(a)各定理的题设条件比较简明、自然;(b)非参数部分的估计是全局性的解析函数;(c)所及光滑参数为多项式的次数,它的确定原则为在样本容量足以支撑的前提下尽量取大,这相较于窗宽、惩罚系数、节点等光滑参数要简易.
本文的叙述分6节.第1节为该文内容、思想概述及有关定义,第2节为回归函数的非参数部分与参数部分估计途径的分离,第3、4节为分别对非参数部分与参数部分的估计,第5节最终给出整个回归函数的估计,其是在L2与强相合之联合意义下收敛的,第6节为佐证该文的理论结果,设计实行了一个模拟实验.
本文用到如下定义.
定义1.1设实随机变量X,Y∈L2(Ω,F,P)[7],记
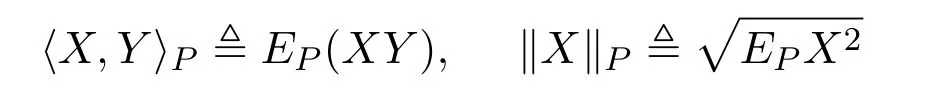
定义1.2若(R,B(R),L)为概率空间,x∈R,∀δ>0成立
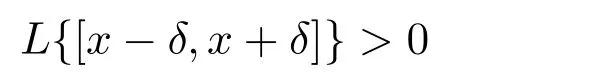
则称x为测度L的增长点.
定义1.3作矩阵的简约记法为

2 非参数部分与参数部分估计途径的分离
定理2.1若Y,X,Z1,···,Zd,W为概率空间(Ω,F,P)上的实随机变量,Y关于X,Z1,···,Zd的回归函数及Y关于X,Z1,···,Zd,W的函数分别为


3 非参数部分的估计
定理3.1若题设同定理2.1,且由X诱导出的测度PX有无穷多个增长点,xn∈L2(R,B(R), PX)(n∈N),PX还满足下列三个条件之一:
(A)代数多项式全体在L2(R,B(R),PX)中稠密;
(B)存在有限区间[a,b]⊂R,使PX{[a,b]}=1;
(C)对Lebesgue测度的密度函数ρ(x)满足存在常数C>0,使ρ(x)≤Ce−x2(x∈R),另记







4 参数部分的估计


5 回归函数的估计
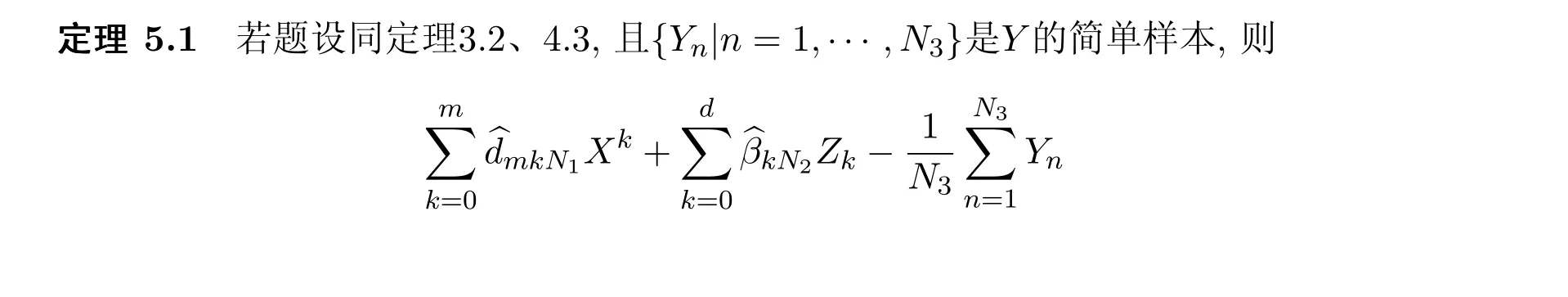

6 模拟实验


表1 参数估计对比
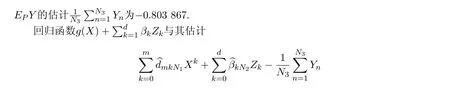
在(Z1,Z2,Z3)分别取值(0.5,1,0.2),(−4,50,12.8)时,它们关于X的函数图象的对比图(不带星号线为被估计函数,带星号线为估计函数)分别为图a,图b.如是结果,可以作为本文理论的佐证.

图a图像的对比图

图b图像的对比图
[1]Engle R,Granger C,Rice J,et al.Nonparametric estimates of the ralation between weather and clectricity sales[J].J.Amer.Statist.Assoc,1986,81:310-320.
[2]Speckman P.Kernel smoothing in partial linear models[J].J.R.Statist.Soc.B,1988,50:413-436.
[3]洪圣岩.一类半参数回归模型的估计理论[J].中国科学:A辑,1991,21(12):1258-1272.
[4]钱伟民,柴根象.半参数回归模型小波估计的强逼近[J].中国科学:A辑,1999,29(3):233-240.
[5]薛留根.半参数回归模型中误差方差估计的Berry-Esseen界[J].数学学报,2005,48(1):157-170.
[6]胡宏昌,胡迪鹤.半参数回归模型小波估计的强相合性[J].数学学报,2006,49(6):1417-1424.
[7]布洛克威尔.时间序列的理论与方法[M].2版.田铮,译.北京:高等教育出版社,2003.
[8]陈乃辉.随机自变量多项式回归函数的估计问题[J].系统科学与数学,2009,29:(3):297-308.
[9]莫国端,刘开第.函数逼近论方法[M].北京:科学出版社,2004.
[10]周民强.实变函数论[M].北京:北京大学出版社,2006.
[11]赵选民.半参数回归模型非参数分量L1模估计的最优收敛速度[J].纯粹数学与应用数学,1997,13(2):6-11.
On separated estimation for semiparametric regression model under independent case
CHEN Nai-hui
(School of Applied Mathematics,The Central University of Finance and Economics,Beijing100081,China)
By using method of best approximation moment estimate,the estimate of non-parameter section for semiparametric regression model is put out and its kind achieve the join of L2convergence and strong consistent, the estimate of parameter section for the model is put out and its kind achieve strong consistent and consistent asymptotic normality.Lastly,a analog experiment is designed and practised.
semiparametric regression model,random functional approximation,moment estimate,consistent asymptotic normality
O212
A
1008-5513(2009)04-0654-11
2008-11-11.
陈乃辉(1959-),副教授,研究方向:概率统计.
2000MSC:62G08,62G20,41A10
