Heisenberg-Virasoro代数的q-形变的量子群结构
2009-07-05程永胜张明亮
程永胜,张明亮
(河南大学数学与信息科学学院,河南开封 475001)
Heisenberg-Virasoro代数的q-形变的量子群结构
程永胜,张明亮
(河南大学数学与信息科学学院,河南开封 475001)
构造了水平为零的扭的Heisenberg-Virasoro代数的一个q-形变Hvirq,证明它是一个quasi-hom-李代数.给出该代数的一个非平凡的量子群结构,即它是一个非交换且余交换的Hopf代数.
量子群;q-形变Heisenberg-Virasoro代数;Hopf代数
1 引言
量子群是在二十世纪八十年代由俄罗斯数学家Drinfeld和日本数学家Jimbo各自独立发现[1],之后它成为数学家和物理学家研究的热门课题.究其原因在于该学科与量子Yang-Baxter方程密切相关,而该方程在共形场论、量子可积系统等研究领域有着非常重要的应用[2].量子群不是群,它是一个非交换且余交换的Hopf代数.
近年来出现了不少有关李代数的q-形变的文章[36].所谓李代数的q-形变就是通过对李代数的结构常数加一个或者多个参数使之广义化,当这些参数趋于1时,李代数的q-形变就回到李代数的情形.一般地,李代数的性质在它的q-形变中还会保持.
有关Virasoro的q-形变的文章很多,关于Heisenberg代数的q-形变的文章也出现过[35].然而有关Heisenberg-Virasoro代数的q-形变及其相应的量子群结构的存在性问题是一个非常有趣的问题,这个问题的解决或许对物理学家很有用.之前第一作者和苏育才教授曾经给出了Heisenberg-Virasoro代数的q-形变的一种实现,并给出其相应的量子群结构,本文我们将构造出Heisenberg-Virasoro代数的q-形变的另外一种实现并给出其相应的量子群结构,这种实现及构造完全不同前者[78].
本文组织如下:第2节先回忆李代数的q-形变的一般定义,然后给出Heisenberg-Virasoro代数的q-形变.第3节给出一个与Heisenberg-Virasoro代数的q-形变的相应的非平凡的量子群结构.
2 Heisenberg-Virasoro代数的q-形变
首先回忆一下李代数的定义.对于复数域C上的向量空间V,定义一个扭映射τ如下

则一个李代数(V,ϕ)是由一个向量空间V和一个双线性映射ϕ:V⊗V→V(被称为V的括积)组成,并且满足下面两个条件

其中1表示V⊗V中的恒等映射,τ12=τ⊗1,τ23=1⊗τ.
现在考虑更广泛的情况.将上面的李代数的定义的反对称性和Jacobi恒等式推广.
定义1[6]一个quasi-hom-李代数由一个三元组(L,φ,ω)组成,其中向量空间L,双线性映射φ:L⊗L→L(被称为L的括积)及映射ω:L×L→LC(L)满足下面的条件

其中(z,x),(x,y),(y,z)∈L⊗L,LC(L)表示向量空间L上的所有C-线性映射的全体.
从定义可以看出,quasi-hom-李代数是一种广义的李代数,它包括李代数,李超代数,ε-李代数及着色李代数等.例如,当ω=−id时就是李代数的情况.
水平为零的扭的Heisenberg-Virasoro代数Hvir最先由文[9]引进,扭的Heisenberg-Virasoro代数是定义在圆上的次数至多为1的微分算子李代数的泛中心扩张
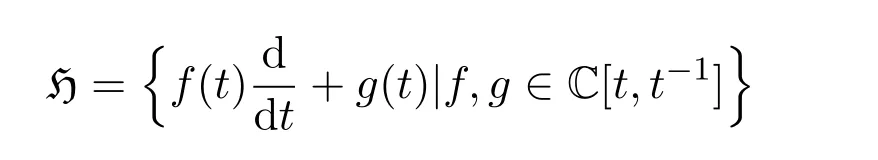
它有一个无限维Heisenberg子代数和一个Virasoro子代数,Virasoro子代数在Heisenberg子代数上的作用是一个2-上循环的自然作用[1013].水平为零的扭的Heisenberg-Virasoro代数Hvir有基CL,CLI,CI,Ln,In(n∈Z)及下面李运算:


由以上推理可得
定理1若向量空间Hvirq有生成元Ln,In(n∈Z),CL,CI,CLI及下面的乘法运算,即(5),(7),(20),(6),(8)和(21)式,则Hvirq依照映射(9)构成一个quasi-hom李代数.
我们称Hvirq是Heisenberg-Virasoro代数的一个q-形变.
3 q-形变Heisenberg-Virasoro代数的量子群结构



[1]Drinfeld V G.Hamlitonian structures on Lie group,Lie algebras and the geometric meaning of classical Yang-Baxter equations[J].Soviet.Math.Dokl.,1983,27(1):68-71.
[2]Drinfeld V G.Hopf algebras and the quantum Yang-baxter equation[J].Soviet.Math.Dokl.,1985,32:254-258.
[3]Hartwig J T,Larsson D,Silvestrov S D.Deformations of Lie algebras using σ-derivation[J].J.Algebra, 2006,295:314-361.
[4]Kassel C.Cyclic homology of differential operators,the Virasoro algebra and a q-analogue[J].Comm.Math. Phys.,1992,146:343-351.
[5]Mansour M,Tahri E H.A q-deformation of Virasoro and U(1)Kac-Moody algebras with Hopf structure[J]. Modern Phys.letters,1999,14:733-743.
[6]Larsson D,Silvestrov S D.Quasi-hom-Lie algebras,central extensions and 2-cocycle-like identities[J].J. Algebra,2005,288:321-344.
[7]Hu N.Quantum group structure of the q-deformed Virasoro algebra[J].Lett.Math.Phys.,1998,44(2):99-103.
[8]Delius D W,Gould M D.Quantum Lie algebras,their existence,uniqueness and q-antisymmetry[J].Comm. Math.Phys.,1997,185:709-722.
[9]Arbarello E,Concini C,Kac V G,et al.Moduli spaces of curves and representation theory[J].Comm.Math. Phys.,1998,117:1-36.
[10]Shen R,Jiang C.Derivation algebra and automorphism group of the twisted Heisenberg-Virasoro algebra[J]. Comm.Algebra,2006,34:2547-2558.
[11]Billig Y.Respresentations of the twisted Heisenberg-Virasoro algebra at level zero[J].Canad.Math. Bulletin,2003,46:529-537.
[12]Su Y.Classification of quasifinite modules over the Lie algebras of Weyl type[J].Adv.Math.,2003,174:57-68.
[13]杨闻起.BCI-代数的拟伴随代数及应用[J].纯粹数学与应用数学,2006,22(2):178-181.
Quantum group structure of the q-Heisenberg-Virasoro algebra
CHENG Yong-sheng,ZHANG Ming-liang
(School of Mathematics and Information Science,Henan University,Kaifeng475001,China)
In this paper,the authors introduce the q-deformed Heisenberg-Virasoro algebra Hvirq,and prove that it is a quasi-hom Lie algebra.In the following,the authors construct its nontrivial quantum group structure, which is a noncommutative and cocommutative Hopf algebra.
Quantum group,q-Heisenberg-Virasoro algebra,Hopf algebra
O152
A
1008-5513(2009)04-0695-06
2008-05-12.
国家自然科学基金(10825101),中国博士后科学基金(20090450810).
程永胜(1973-),博士,研究方向:李代数.
2000MSC:17B37,17B62
