巧妙引导 掌握连比

席旭光

“连比”是两个以上的部分量的连续相比。它反映了各部分所占份数与总份数之间的关系,但连比不是连除。教材中对连比没有作具体的介绍,仅在练习中编排了一道含连比的题目,这说明不要求学生对连比有更多的了解,但又没有舍弃。然而,在近年各地小学毕业(升学)考试的数学试卷中,屡见应用连比解决实际问题的试题,还有一些化成连比能巧解较复杂的分数、百分数或比的应用题。可见,连比应用广泛而简捷,让学习有余力的学生掌握它,将会提高他们解决问题的能力。

1.求三个数连比的方法

一般的,如果甲、乙两数的比是a∶b,乙、丙两数的比是b∶c,那么,表示甲、乙、丙三个数的比可以写成a∶b∶c。a∶b∶c就叫做甲、乙、丙三个数的连比。怎样由两个相关的比求出三个数的连比呢?可分以下几种情况讨论:

①如果前一个比的后项和后一个比的前项相同,可把两个比直接写成连比。

如:甲∶乙=3∶2,乙∶丙=2∶4,甲∶乙∶丙=3∶2∶4。

②如果前一个比的后项和后一个比的前项成整倍数关系,可利用比的基本性质把其中一个比变形后,再写成连比。

如:甲∶乙=3∶4,乙∶丙=2∶1,甲∶乙∶丙=3∶4∶2。

③如果前一个比的后项和后一个比的前项既不同,又不成倍数关系,那么可利用比的基本性质把两个比变形。

如:甲∶乙=3∶5,乙∶丙=7∶8,求甲∶乙∶丙。

只要把两个比中表示乙的份数化成相等即可。

甲∶乙=3∶5=(3×7)∶(5×7)=21∶35;

乙∶丙=7∶8=(7×5)∶(8×5)=35∶40;

所以,甲∶乙∶丙=21∶35∶40。

2.应用连比解决问题举例

例(1) 商店运来橘子、苹果和梨一共290千克,橘子和苹果质量的比是5∶6,梨的质量是苹果的1/10。橘子比梨多多少千克?

分析与解:此题一般解法是把比化成分数,先求出苹果的质量,然后分别按“5∶6”、“1/10”求出橘子和梨的质量,最后才能求出橘子比梨多的千克数。这样解步骤多,且计算麻烦。

运用连比可这样解:把题中的“1/10”转化成梨和苹果质量的比是1∶10,然后按右边求连比的方法求出:橘子∶苹果∶梨=25∶30∶3。题中三种水果共290千克相当于(25+30+3)份,要求橘子比梨多的千克数相当于(25-3)份,这样很易求得橘子比梨多290÷(25+30+3)×(25-3)=110(千克)。

即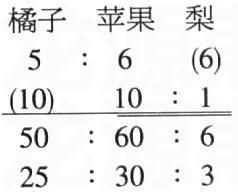

例(2) 袋子里红球与白球的个数之比是3∶2,放入若干只红球后,红球与白球数量之比是9∶4;接着放入若干只白球后,红球与白球数量之比是6∶7。已知放入的白球比放入的红球多7只,那么,原来袋子中有白球多少只?

分析与解:这道题数量关系复杂,且比较抽象,一般化成分数求解,思路繁杂,步骤甚多,属于竞赛类难度较大的题目。但若运用连比求解,思路则简捷明了。

根据:原红球个数∶原白球个数=3∶2=6∶4

放红球后个数∶原白球个数=9∶4

可求:原红球个数∶原白球个数∶放红球后个数=6∶4∶9

再根据放入若干只白球后,放入红球后个数∶放入白球后个数=6∶7,可得四个数量的连比:原红球个数∶原白球个数∶放入红球后个数∶放入白球后个数。

6 ∶ 4 ∶ 9 ∶ (9)

(6) (6)6 7

即 12 ∶ 8 ∶ 18∶21

显然,放白球个数占21-8=13(份),放红球个数占18-12=6(份),则放入白球个数比放入红球个数多7只,相当于13-6=7(份),而原白球个数占8份,所以原白球有7÷(13-6)×8=8(个)。

3.结语

当前适逢数学教学改革,如何掌握连比,除了本文提出的一些方法外,还有许多方法,类似的例子也还有很多。由以上例子就足以看出运用连比解答含两(三)个分率(比)的较复杂题的优越性,且思路清晰,计算十分简便,易于理解和掌握。我们在教学中不仅要教给学生解题的技巧,更重要的应该在于数学思想方法的教学。