从策略性知识的特点谈解决问题策略的教学

沈　超

众所周知，新课程教材中已不再有“应用题”的用语，这并不是因为教材中不再有这样的题型，而恰恰相反，作为数学知识呈现与应用的主要方式，应用题在教材中随处可见。当然，新教材已不再将应用题作为一种独立的知识体系编排，而是作为解决问题的载体纳入数学问题解决教学范畴，这大大超越了应用题作为“解题”的教学功能。这一变化体现了应用题教学价值观的转变，即从过去的学会“解题”，转变到获得“策略”，形成一般的解题能力——“让学生经历观察、分析、操作、交流、实践等学习活动，以及在这些活动中开展比较、综合、抽象、概括等数学思维活动，积累解决问题的经验，获得用数学解决问题时广泛使用的方法和策略。”

新课程对应用题教学的重新定位，使儿童学习应用题由过去的主要获得“程序性知识”转变为主要获得“策略性知识”。然而，这样的转变被一些教师误读或不理解。

学习心理学将数学知识分为三类：陈述性知识、程序性知识和策略性知识。虽然，对“策略性知识”的界定有不同观点，但公认的是，这种知识不同于前两类知识的外在性，是数学学习活动本身在主体的内在反映。“策略性知识”（又称认知策略）侧重于数学学习或问题解决过程中蕴涵在“事实性知识”背后的内在方法，表现为学生对自己在解决数学问题时的信息表征、组织、贮存、提取方式及对思维过程的调节和监控。它主要有两个特点：①作用方向不是“对外办事”，而主要是“对内监控”。即策略性知识的作用对象不是外在的“数学事实”，而是主体的主观内部数学信息加工过程。②基本功能是解决怎么办，即如何学才最好、最有效的问题。比如，在解决应用问题时．运用何种公式（或数量关系式）、采用什么解题步骤与格式是陈述性知识和程序性知识解决的；如何有效地获取数量信息、采取什么方式处理与分析数量信息间关系、建立何种有效的数学模型解决，以及解决问题方法的普遍意义等是靠策略性知识来完成的。

认知心理学认为，策略性知识的掌握需要经历三个阶段：一是了解阶段。在这个阶段，策略性知识以陈述性知识的形式被学生学习，学生首先需要理解有关概念、规则、事实和解决数学问题的步骤等，并纳入到个体的知识结构中。二是知识转化阶段。这一阶段通过多次应用上述知识，使策略的陈述形式向策略的程序形式转化，即每当遇到同类任务时，就能用同一策略去解决。此时，相应的策略已经开始支配学生，策略性知识开始内化，外在的策略开始向内在的、个性化的、自己的策略性知识转化。三是策略熟练应用阶段。策略性知识完全支配人的学习活动，可以达到自动化的水平。这说明，“策略”在开始阶段也具有外在的形态，经由内化过程而形成个体的策略性知识结构。

长期以来，小学数学教学重视对陈述性知识和程序性知识的教学，忽视对策略性知识的教学与研究，教师对策略性知识的教学大多不是有意为之。以应用题教学为例，追求的是学生能按照一定的程序解题，而较少考虑在解题中获得一般的策略。新课程将应用题教学纳入“解决问题”范畴，定位于学生获得策略性知识。然而，由于对策略性知识理解的偏差，一些教师将“田忌赛马”（编在人教版数学课本中，体现一种科学的思维方式）和“打折购物”（例如，某商场搞促销活动，方法一：满500送200；方法二：满300送80；方法三：打7折。妈妈准备在服装柜买1750元的商品。如果三种方法只能选用一种，怎么买最合算?）式的解决问题的技巧理解为“策略性知识”中的主流。致使有些教师对“解决问题的策略”感到很神秘，甚至无所适从。其实，应用题教学中的“策略”大多是老师们在以前的教学中行之有效的方法。对此，我们没有理由放弃。在新课程实施近一轮的今天，我们仍然理直气壮地、创造性地继续发挥其作用。

1.审题中的策略

审题是一个提取有效信息（主要是数量信息）的过程，更是从生活问题转化为数学问题的关键步骤。

审题的实质就是把握“问题”要素。对应用题而言，要素包含四方面：数据——直接或间接给出的量值；关系——量之间的逻辑关系与运算关系；状态——情境状态；目标——问题的定向系统。

让学生学会审题，就是掌握不同数学背景下合理选择不同的信息获取策略。

①实物模拟操作。这里的“实物”通常是小棒、纸片等学具。如：“姐妹二人做了相同朵数的花，姐姐给了妹妹3朵后，妹妹比姐姐多几朵?”学生凭直觉会得出“多3朵”的结论。操作一下，数量间关系一目了然。

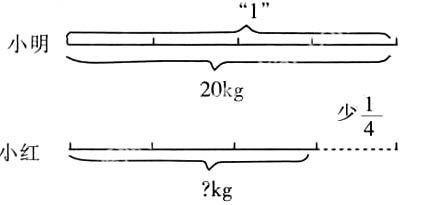
②画图（模拟图、示意图、集合图、线段图等）。画图就是将题目要素直观呈现在图上。利用图形直观既体现了数形结合，更是思维方式转换的需要。它使抽象、隐晦的数量关系具体化，是理解题意最常用的直观辅助手段。目前有些教师忽视甚至放弃对学生用画图分析能力的培养，这是不应该的。当然，作图的形式允许学生选择，作图的要求也不能像过去那样过分规范，避免再成为学生新的负担。比如分数应用题的线段图，过去过分强调“分率”在上、具体量在下，该画一条还是两条、“比多少”时画虚线还是实线等等都有“规矩”（如图）。现在，教师仍然可以这样画，但对学生就不必要求过严。

③摘录条件问题。对有的题，图并不能直观反映数量变化规律，有规律地排列条件与问题是审题更有效的策略。比如“归一”应用题。

④列表。这是对数量具有按“批”规律出现的题一种有效的审题策略。

⑤联想。利用生活经验或在头脑中“操作”。这是思考问题一种常用的“直观”方式。

上述策略在审题目中都是十分有效的，但由于新教材中信息呈现的方式比过去的题丰富得多，如何体现“多样”与“自主”才是老师们需要优先考虑的。

2．分析数量关系中的策略

数量关系是指数学问题中已知量与已知量、已知量与未知量之间具有运算意义的逻辑联系。应用题的数学本质就在于其数量关系。可以说，解题思路的探求过程就是对数量关系从不明了到明了的过程；理解数量关系的过程也是运用各种策略的过程。

分析数量关系的策略十分丰富。一般的策略包括“综合法”与“分析法”、“归纳”与“演绎”、“寻找中间问题”等等。对这些策略的使用，不能再像过去那样简单地作为“工具”教给学生，而应该有意识地在教学过程中始终运用，潜移默化地引导学生有条有理地分析。随着熟练程度的提高，作为一种习惯性的数学思维方式成为学生认知结构中的一部分。

特殊的策略则不胜枚举，如，等量代换、数形结合、化归转化、逆向思考、猜想验证、比较异同、方程思想、模拟假设、对应联想、列举寻源等等。这些策略的运用要因题制宜，除了体现多样化与个性化，教师更应该有意识地引导归纳、比较优劣、灵活应用。

3.列式计算中的策略

（1）算式的多样性与合理性问题。在倡导算法多样化的今天，应用题不同的解题思路会形成不同的算法（算式）。在鼓励学生多角度思考、多样化列式的同时，既要重视对多种解法作合理性比较，也要注意列式策略不“误入歧途”。有这样一则教学案例：“每个书包11元，32元可以买几个这样的书包?”算式为32÷11=2（个）……10（元），答案是可以买2个这样的书包。这时，有学生提出32元可以买3个这样的书包，其理由是买多了可以与售货员讨价还价便宜这1元；有的说可以打折；更有学生提出“可以到别的商店去买”。于是，讨论各种买包的策略成了解决问题的关注点。题目在教师“会创造”的赞扬声和学生的掌声中结束。“生活化”固然给了学生很大的想象空间，但在这样的教学中，小学生学数学本应遵循的许多规矩不存在了，这不利于学生数学策略性知识的学习和儿童科学精神的养成。

随着应用题开放性的增强，现实问题不仅算式多样，有些还无固定答案，对此，要引导学生从信息的利用和答案的合理性角度作算式的优化。

（2）提炼数量关系式的策略。算式以最直接的形式反映了题目的数量关系，“数量关系式”则是对解决同类现实问题具有一般意义的数学模型。对提炼数量关系式不应该遮遮掩掩，因为这既是一个寻找规律的过程，也是获得同类问题解决方案的一个通用策略。当然，要注意两点：①归纳数量关系式不是解题的最重要目的，并且区别于过去的应用，关系式不再仅仅是可以套用的一个公式。②数量关系式有两种类型：情景（常识）型关系式（如“单价×数量=总价”、“工作总量÷工作效率的和=共同工作时间”）；纯数学术语表征的关系式（如“每份数×份数=总数”）。对于前者，作为“现实问题”向用“数学方法解决”过渡的桥梁，这些关系式无疑是十分重要的，归纳、记忆与应用仍然不可忽视。而对于后者，就不一定出现这样的式子，更不用让学生背诵，而可以结合具体题目，逐渐经历抽象过程。比如，“3束花，每束4朵，一共几朵”：每束4朵，“乘”3束，一共12朵→每束朵数乘束数等于总朵数→每份数乘份数等于总数。

4.检验与反思中的策略

检验与反思是应用题作为解决问题目标的重要内容，是学生自我评价的主要方式。要引导学生掌握检验与反思的一些策略，并成为学生的自觉行为。策略性知识就是在这种有意识的自我反省中形成的。

反思最主要的形式是回顾解决问题的全过程，这同样需要教师的引导：“解决这个问题经历了哪几个步骤?”“解决问题的过程中你运用了什么策略?”“能解释一下你的想法吗?”“能不能换个角度思考?”“还有更好的方法吗?”“有什么新的问题?”“这个问题的结果是否合理?”等等。比如，对解题思路的叙述是展示学生思维过程的重要方式，能促使学生从直观感知上升到数学理解。因而，仍然有必要让学生有条理地叙述，“根据……可以知道……”，“先……再……”等。虽然不必再追求形式，但要强调说清楚，同学能听清楚。又如，对于答案合理性的检验，要让学生掌握根据不同问题特点采用“生活常识法”“逆运算法”等策略。

从学会解题到经历解决问题的过程，应用题教学需要实现从程序性知识到策略性知识教学的转变。对此，教师的认识正在逐步完善，而面临的问题仍然不少。比如，①应用题大多融于计算教学中，在这样的课堂中，解决问题的策略教学与计算技能培养关系的度如何把握?②一定量的重复练习是掌握策略的必要步骤，而过多的重复练习又有重回套类型老路之嫌，多少量的练习是恰当的?③对学生学业的评价如何体现学生的策略性知识掌握水平?等等。这些需要各方的共同探索。让传统教学的优势在新课程体系中得以体现，仍然应该是我们努力的方向。