例谈数学操作性实验课

凌 玲

长期以来，人们一般认为“实验”只是物理和化学的事，与数学无关。其实，数学中的许多概念、定理、公式都是通过实验发现的。

数学概念、定理的形成一般来自于解决实际问题或数学自身发展的需要，教材上常常隐去其形成的思维过程，而通过实验可以再现这些过程。教师在教学时，要根据需要设置合理情境，巧搭数学实验平台，引导学生参与数学概念、定理的形成过程，使学生在动手中弄清概念、定理的来龙去脉，从而能对其加深理解，准确把握。数学的实验课有操作性实验课、思维性实验课、计算机模拟实验课等几种类型。本文略谈数学操作性实验课的教学方法。

操作性数学实验教学是在一定的情境中，引导学生通过对一些工具、材料的操作，探索数学知识，检验数学结论(或假设1。这种实验常用于与几何图形有关的知识、定理、公式的探究或验证。操作性实验教学的一般步骤是：教师提出问题→学生实验→观察分析→猜想结论→交流校正→验证或证明。

譬如，在学习椭圆时，可以这样引导学生通过实验操作来探究椭圆的概念：全班每两个学生分为一组，课前准备两枚图钉、一根细线、一张白纸、一支铅笔，课堂上按以下程序进行操作、思考。

试验一：取适当长度(2α)的细线，在细线两端系上图钉，将图钉分别按在铺有白纸的桌面上两点F₁、F₂、处，F₁与F₂距离的选取满足｜F₁F₂｜<2a，用铅笔靠在细线上并拉紧细线，转动一周，画出一个椭圆。

作完图以后，要求学生思考如何给出椭圆的定义。其中，教师可适当提示在作图的过程中，哪些量是变化的，哪些量是不变的，引导学生发现动点、定点和定长，并进一步发现所画曲线上的每个点具有的共同特征。

试验二：改变细线的长度，使2α=｜F₁F₂｜，按照试验一的方法操作铅笔，能得到什么结论?

试验三：改变细线的长度，使2α<｜F₁F₂｜，按照试验一的方法操作铅笔，出现什么现象?

学生们会发现，当2α=｜F₁F₂｜时，画不出椭圆，只能得到一条线段；当2a<｜F₁F₂｜时，画不出任何图形。此时，要求学生思考，椭圆的完整定义是什么，让学生自己体验在椭圆定义中加入2a>｜F₁F₂｜这个限制条件的必要性。

在讨论椭圆的离心率的时候，可以在前面画椭圆实验的基础上，设计以下试验：

1F₁、F₂位置不变，在满足条件2a>｜F₁F₂｜的前提下，改变2n的长度，作出椭圆的图形，并比较这些椭圆的形状有什么不同。

2细线长2α不变，在满足条件2a>｜F₁F₂｜的前提下，改变F₁F₂的位置，作出椭圆的图形，并比较这些椭圆的形状有什么不同。

通过这两个试验，学生们发现，有些椭圆的形状比较“圆”，有些比较“扁”，而这显然与细线长2α、｜F₁F₂｜即焦距2c有关。进一步再引导学生通过探讨得出：当c与α相比很小，即离心率e=c／a越接近0的时候，椭圆越“圆”；当c与α越接近，即e=c／α越接近1的时候，椭圆越“扁”。

在上述实验过程中，椭圆的概念、性质不是作为结果直接告诉学生的，而是通过学生动手操作、探究获得的，这是一个主动构建知识的过程，在这一过程中课堂真正还给了学生。学生之间的分工协作，既加强了数学交流，培养了团队合作精神，又使学生思维的深刻性得到加强。

又如，在概率教学中学习等可能事件的时候，可以引进按以下步骤进行的实验：

步骤一：创设情境，提出问题

本周末有个学术报告会，小张和小王都很想去，但是只有一张票，大家能否帮小张、小王想个办法来决定谁去听报告会。甲同学建议采取掷硬币的办法，任意抛出一枚均匀的硬币，若其正面朝上，小张去，若反面朝上，则小王去。大家想一想：这个办法公平吗?

步骤二：进行实验，收集数据

1同桌两人做20次掷硬币的游戏，一人掷硬币，一人负责记录数据，两人合作借助计算器计算硬币正面朝上的频率和反面朝上的频率，并填写记录表格。

2汇总各组实验数据，累计全班同学的试验结果，分别计算试验累计进行到20次、40次、80次、120次……400次时硬币正面朝上的频率，并完成折线统计图。观察这个统计图，你发现了什么规律?

步骤三：验证猜想，形成概念

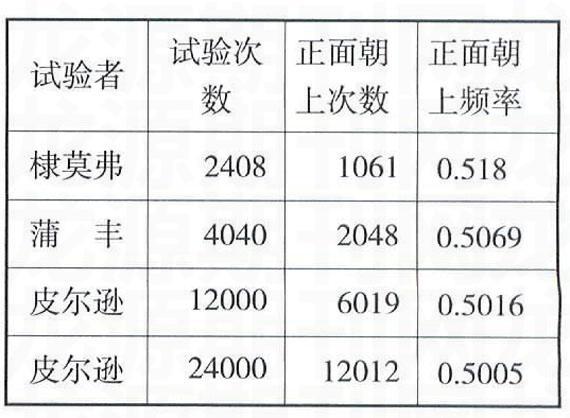
以下是几位数学家所作的掷硬币试验的数据统计，它与你所发现的规律相符合吗?

通过这个实验让学生体会到：任意掷一枚均匀的硬币，在大量重复的实验中，它正面朝上的可能性和反面朝上的可能性都相等，都趋向于0.5。由此引出“等可能事件”和“概率”的概念。

在数学实验中，学生由于亲自动手操作，从一个旁观者和听众变成了一个参与者，因此，学生对实验的结果、产生结果的原因、涉及的新知识、方法等产生强烈的兴趣，这就有利于培养学生的创新思维。另外，在实验中还涉及很多数据和实验信息，学生通过几个不同范围的合作互动，探索出实验的结果，从而培养了学生搜集、处理信息的能力以及合作精神。

(责编王学军)