数学课上要力求做到“三多”
2009-04-21朱春雷
朱春雷
学生的数学学习过程是一个以学生已有的知识和经验为基础的主动建构过程,只有学生主动参与到学习活动中,才是有效的教学。数学教学是数学活动的教学,组织有效的数学教学活动,是数学课堂教学改革的重要目标,也是构建素质教育数学课堂教学模式的关键性环节。在教学实践中要想达到上述目标,数学课上必须做到三点:学生说的话要比老师说的话多;思考训练的时间要比说话的时间多;学生的数学活动要比教师的讲解总结多。下面就结合课例具体阐述。
第一,学生说的话要比老师说的话多
课堂教学中,教师的教是为学生的学服务的。当然,课上教师要用语言去组织教学,要启发学生,还有必要的知识传授,因此教师的说也是必不可少的,也要用去一定的时间。一堂课的时间是一定的,除了说话,还有其他事要做,有限的说话时间必然会出现谁多说谁少说的问题。我想,老师应当把说话的时间给学生多些,让学生自己拥有话语权,要让每个学生都有发言的机会,并促进每个学生都去争取发言,这也就是学生说的话要比老师说的话多。老师说的话虽然少了,更要注意该说的话的表达,如启发的话,点睛的话,要力求言简意赅、恰到好处地表达,可说可不说的话不要说,学生会说能说的话不说。下面我们就利用《乘法分配律》教学实例来比较在成功课堂上老师说的话和学生说的话。
电脑出示:一件儿童上衣的价格是5元,一条儿童裤子的价格是4元。买3套儿童服装应付多少钱呢?
师:你能用几种方法解答?请列式计算。(生各自独立计算,不一会儿,纷纷举手)
生1:我先算出一套服装的价钱,再求出三套的价钱,算式是括号5加4括号乘以3。还有一种方法是先分别算出三件上衣和三条裙子的价钱,再算出三套服装的总价钱。算式是5乘以3的积加上4乘以3的积。(结合学生回答教师板书:(5+4)×3;5×3+4×3)
生2:我的方法是:5+5+5+4+4+4=27
生3:我的方法是:5+4+5+4+5+4=27
生4:我觉得这两个同学的想法与前面同学的两种想法是一致的。但是上面的算式比较简便。大家都同意生4的意见。
出示:小强摆木块,每行摆6个绿木块,9个红木块,共摆了4行。
师:小强一共摆了多少个木块?你能用几种方法解答?
学生再次列式计算,并很快说出两种不同的思考方法和算式,结合学生的回答,教师接着上题板书如下:(6+9)×4;6×4+9×4
对于上述两题,老师只用一句问话:你能用几种方法解答?而学生在经历了两种不同思考方法的计算后,并用多种方式表达出来,且在讨论和表达中,发现新的知识规律。同时,产生一种体验,乘法分配律的知识存在于实际问题的解决中。
第二,思考训练的时间要比说话的时间多
数学的学习在于思维的训练,在于做数学。因此老师的功夫体现在如何促进学生有兴趣、有深度的思考上,教师在学生的思考上和做数学上要舍得花时间。
接上面《乘法分配律》案例看看学生在老师启发引导下的思考和训练。
师:从上面的算式中你有没有发现什么规律?
同学们的双双眼睛注视着黑板上的算式,在寻找着其中的规律。渐渐地,一些学生举起了手,有些学生开始有些激动,急着与周围的同伴说起了悄悄话。此时,教师没有急于指名回答,而是示意学生继续认真思考。
又过一会儿,师才说,你们真的发现了这些算式里隐含着的规律,请与你的同桌交流一下好吗?
教室里的气氛顿时热烈起来了,同学们之间指点着、交流着,一些心急的同学忍不住又高举着小手。
师为了让学生进入学数学和做数学的过程,没有让学生发言,而是让他们做另一件事。师说:从大家的神态和脸部表情中,老师知道你们一定觉得自己发现了什么规律。同学们,你们发现了什么,我能猜到。不过,你们所看到的也许只是一种偶然现象,是一种猜想而已。你们能再举些例子对自己的猜想进行验证吗?
同学们认真地在本子上任意地写算式,进行着计算。很快他们举起了手,积极汇报自己验证的结果。
生1:(7+2)×4=7×4+2×4
生2:(1+6)×7=1×7+6×7
生3:(3+9)×5=3×5+9×5
师:从同学们举的大量的例子中,可以确定你们的发现是正确的。
有生说:老师,虽然举了许多例子,可万一还是碰巧,怎么办?他的话引起了不少同学的赞同。
师:会有这种“万一”吗?你能举出一个反例吗?
教师的反问,引起了同学们的深入思考……
有生说:不可能有反例出现。以“(7+2)×4=7×4+2×4”为例,左边算式括号内是9,表示有9个4,右边算式的“7×4”表示有7个4、“2×4”表示有2个4,加起来共有9个4。等号两边的算式形式不同,但它们的意思是相同的,都表示9个4,所以是相等的。其他的式子里道理也是一样的。
师:同学们还有不同意见吗?生摇头以示没有意见。
师:你们发现的这个知识规律,叫做乘法分配律。什么叫乘法分配律?请同桌再交流一下。
学生积极地与同桌交流,又踊跃参加集体讨论。
生l:把括号里的两个数加起来后乘以一个数,等于把括号里的两个数都去乘以一个数,再把乘出来的积加起来。
生2:乘法分配律是:左边把两个数加起来乘以乘数,等于括号里的一个加数乘以乘数加上括号里的另一个加数乘以乘数。
师:你们想表达的是这样的意思吗?师板书:两个数的和与一个数相乘,可以用两个加数分别与这个数相乘,再把两个积相加,结果不变。
师:这叫做乘法分配律。能用字母来表示乘法分配律吗?结合学生回答,教师板书:(a+b)×c=a×c+b×c
对于乘法分配律的教学,教师没有把重点放在数学语言的表达上,反复地进行所谓的严格、准确和简明的表达,而是把重点放在学生通过多种方法的计算去完整地感知,对所列算式进行观察、比较和归纳,大胆提出自己的猜想并举例进行验证……只有经过这样的探究活动,学生才会真正有所体验,才能建构自己有意义的知识,用语言表达乘法分配律也就水到渠成。这个过程也就是学数学、做数学、数学化的过程,也就是建构数学模型的过程。
第三,学生的数学活动要比教师的讲解总结多
教师讲、学生听,教师演示、学生模仿的教学在新的教学理念下,肯定是不行的。但在学生积极参与数学活动基础上的,教师的必要讲解和总结却又是不能少的。教师的讲解和总结在于引起思考、调动学生参与数学活动、画龙点睛和提升主题。如何通过自主、合作、探究性的学习活动激起学生有效学习是当前课堂教学应该优先、突出考虑的问题。
以《正、反比例的意义》教学实例为例阐述学生的数学活动和教师的讲解总结。为了便于较好地参与数学活动,教师特以改变教材的呈现形式,把正反比例的意义放到同一课时进行。本课重要的理念就是为学生提供“做”数学的机会,让学生在学习过程中去体验数学和经历数学。
教师对学生自主、合作、探究性的学习活动进行有效的设计。
在导入以后,学生进行第一个数学学习活动。(探究合作,初步感知)
教师出示下列表格:
①一辆汽车每小时行驶60千米。
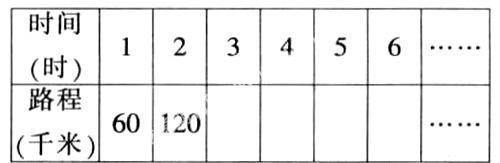
②工厂加工600个机器零件。
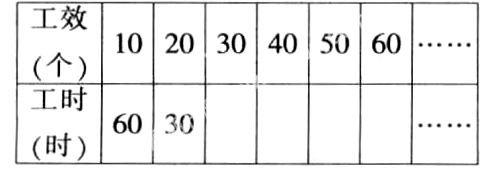
学生自己填,集体校对填正确。
师:在填写表格的过程中,不少同学已经感觉到两个表格中数据的变化情况有所不同,下面我们就进一步研究它们到底有什么不同。请各小组同学合作完成下面的问题:
①找一找:表中有相关联的量吗?如果有是哪两种?
②想一想,一种量发生变化,另一种量是怎样随着变化的?
③算一算:计算相对应的每组数的和、差、积、商。看看有什么发现。
学生分前后四人一组合作学习,教师行间巡视,并相机参与学生的小组讨论。
师:我们一起来讨论上述问题。
生1:有相关联的量,分别是时间和路程、工效和时间。
生2:两个表中数据的变化情况不同。表1一个量变大,另一个量也变大。表2一个量变大,另一个量反而变小。
教师简要总结,并用箭头在黑板上形象表示。
师:讨论第三个问题前,请同学们先把算式写出来再讨论。
选择几个同学到黑板上分别写出表1的除法和比的不同算式,表2的乘法算式。
师:他们写得对吗?观察这些算式,你们有什么发现?
生3:表1中几组相对应的数的商或者比值是相同的。
生4:表2中几组相对应的数的乘积是相同的。
师:你们知道这些相同的商或者积,实际上是什么量吗?
生5:汽车的速度和零件的总数。
师:谁能把大家的发现概括一下?
学生用自己的语言进行表述,教师总结并板书,表中相关联的两种量的变化规律分别是:路程÷时间=速度(一定)和工效×时间=总量(一定)
