遗传算法在船舶电缆布局优化设计中的应用研究

汪雪莲 黄 君

中国舰船研究设计中心，湖北武汉430064

遗传算法在船舶电缆布局优化设计中的应用研究

汪雪莲 黄 君

中国舰船研究设计中心，湖北武汉430064

船舶电缆布局优化是实现船舶布线自动化的一项技术难题，这一问题的解决可节省大量电缆布局设计的时间和费用。建立优化模型，并对传统遗传算法中初始种群的产生方法、选择算子及变异算子进行改进，增加检测操作，从而构造求解该模型的改进遗传算法。仿真结果表明，该算法是一种具有全局寻优能力的布局优化方法，具有高效性、实用性，并可扩展于解决船舶设计中的其它优化问题。

遗传算法；优化；电缆敷设；船舶

1 引言

船舶设计中存在复杂的电、气、液缆线或管路布局设计（简称“布线设计”）问题。布线设计不仅直接影响布局空间的结构设计、线路总长度和总费用，而且还关系到整个系统的可靠性、可维修性和电子设备间电磁兼容性等。由于船舶线路数量庞大、约束复杂，因而布线设计非常困难与耗时。可以看出，实现布线设计的自动化和优化对提高船舶设计质量、缩短造船周期有着重要的意义。本文所要解决的问题就是在大型CAD系统CADDS5中，实现自动布放电缆功能时所遇到的路径分配的全局优化问题（简称“电缆布局优化问题”）。这里的全局优化是指，在已铺设好的电缆通道网络中，给定电缆的起止结点 （即终端电子设备），如何分配各根电缆的路径以使布放电缆的总费用最低，并保证不超过各通道段的容量限制。

近年来，以遗传算法、模拟退火、禁忌搜索以及人工神经网络为代表的智能优化技术发展迅速，受到人们普遍关注。其中，遗传算法是基于进化理论发展起来的一种广为应用的、高效的优化算法，它以其优良的计算性能和显著的应用效果而特别引人注目［1］。本文给出了电缆布局优化问题的数学模型，并选用遗传算法进行求解，同时对传统遗传算法中的诸多方面进行改进，仿真结果证明了该算法的有效性。

2 遗传算法的基本原理

遗传算法（Genetic Algorithm，GA）是由美国科学家John Holland［2，3］提出来的，它是以自然选择和遗传理论为基础，将生物进化过程中适者生存规则与群体内部染色体的随机信息交换机制相结合的一种概率搜索算法。

用遗传算法求解问题的一般步骤如下：

1）确定染色体（即个体）的编码方案，将解空间的解数据通过编码表示成遗传空间的基因型数据串；

2）随机产生一个初始群体，群体中每个染色体都满足约束条件；

3）计算每个染色体的适应值；

4）选择进行交叉和变异的父代染色体，即把当前群体中的个体按与适应值成比例的概率复制到新的群体中，用于提高群体的平均适应值；

5）对选出的染色体进行交叉操作，即从交配池中随机选取两个个体作为父代串，交换父代串中的若干基因位，得到两个新的子串，用于产生新的个体，保持群体的多样性；

6）对选出的染色体进行变异操作，即以很小的概率随机地改变个体上的某些基因位，用于进一步增加和恢复群体的多样性；

7）重复3）～6）条直至满足终止条件。

3 问题描述及数学建模

本文要解决的船舶电缆布局优化问题，就是在已铺设好的电缆通道网络中，在考虑通道容量约束的条件下，实现电缆路径的最佳分配从而使布放电缆的总费用最低。

这里，电缆通道网络可表示成一个加权无向图G（N，E），其中N表示结点数，E表示连接结点的通道数。假设在该图中共需布放S根电缆，则上述布线问题就可转化为具有S个变量，E个约束条件的组合优化问题，具体数学模型如下：

式中，i为电缆编号（i＝0，1，…S－1）；qi为电缆i所需容量，这里指电缆的横截面积 （即截面大小）；pi为电缆i每单位长度所需费用，这里假设电缆每单位长度的费用与电缆截面大小成正比，为简单起见，取电缆所需容量值为电缆单位长度费用，即pi＝qi；Xi为电缆i所选定的路径矩阵，即Xi∈｛Xi1，Xi2，…，Xin｝，n为电缆i的候选路径数目，其中Xij（j＝1，2，…，n）为电缆i的第j条候选路径矩阵，Xij＝［I1，I2，…IE］T，Ik∈｛0，1｝，0表示电缆i不经过第k段通道，1表示电缆i经过第k段通道（k＝1，2，…，E）；L为通道段长度矩阵，即L＝［L1，L2，…LE］；Q为通道段容量矩阵，即Q＝［Q1，Q2，…，QE］T；C为布放电缆的总费用。

4 改进遗传算法的构造

针对传统遗传算法的不足，本文构造改进遗传算法来求解上述数学模型。

1）确定染色体编码方案

首先对每根待布放电缆的所有候选路径按长度从小到大进行编号，然后将每根电缆的每条候选路径的编号视为一个基因，这样由所有电缆的某条候选路径编号所组成的序列，就可以作为一个染色体，即一种电缆布放方案。例如表1，染色体（0，0，0）表示3根待布放的电缆（AB、AC、AD），均取编号为0的路径 （A→B、A→E→C、A→E→C→D），即全部选取最短路径。为简单起见，本文所有表中的数据均不带单位。

表1 电缆布放方案编码

2）产生初始种群

理论上，初始种群可以随机选取，这也是最常用的办法。但就本文布线问题的特点而言，在最终的解决方案中，即在全局最优路径中必然包括了某些单根电缆的最短路径。所以本文先对每根电缆的所有候选路径按长度从小到大排序，然后按概率为每根电缆指定初始路径：

式中，n为当前电缆的候选路径数目；i为候选路径编号，i＝0，1，…，n－1。

这样编号越小的路径，即长度越短的路径被选中的概率就越大，从而有利于更快速地找到合适的解。本文设种群规模（即群体中个体数目）为100。

3）计算每个染色体的适应值

对于每个染色体所对应的路径方案，要判定其优劣，一是要看其是否满足问题的约束条件，即判断每种电缆布放方案的每段通道实际占用容量是否不超过最大容量的限制；二是要计算其目标函数值，即计算每种电缆布放方案的总费用。

4）选择操作

在应用遗传算法解决实际问题时，有时会出现早熟收敛现象，即种群中的大部分个体都在某一个局部极值附近［4］。过早收敛的主要原因是超级个体的存在，这些超级个体的适应值要比种群的平均适应值大得多，以至于它们拥有大量的后代。由于种群规模是固定的，它们就会阻止其他个体的子代在下一代中出现。经过不多的代数，一个超级个体可能会排除其他有希望的染色体，并造成快速收敛到可能是局部的最优解。因此，必须设计可调节选择压力的算法。本文根据Baker［5］和Whitley［6］等人提出来的基于“排名”的选择方法，设计了一个符合本文布线问题特点的选择机制，其步骤如下：

（1）排除完全重复的个体；

（2）对剩下的互不相同的个体按照目标值从小到大排序 （假设ni为第i个个体的序号，i＝1，2，…，h；h为互不相同的个体总数）；

（3）找到满足约束条件并且目标值最小的个体即当前最优解（假设其序号为nk）；

（4）对于序号小于nk的个体，执行ni＝nk－ni；对于序号大于或等于nk的个体，执行ni＝ni－nk；

（5）按概率选择用于繁殖下一代的个体：

式中，m为经过第（4）步序号变换后最大的序号值。

上述步骤（1）是为了避免已经拥有大量后代的个体繁殖出更多的后代，从而保证种群中个体的多样性。步骤（4）是基于当前最优解调整所有个体的序号，使目标值越接近于当前最优解的个体其排序就越靠前。步骤（5）中的个体选择概率可以使目标值越接近于当前最优解的个体其繁殖机会越大。

5）交叉操作

本文采用了一般的简单交叉算子，而交叉概率则根据不同情况是可变的。当种群中符合约束条件的个体数目很少时，使用较大的交叉概率使个体更新更快从而产生更多的新个体；当种群中符合约束条件的个体数目较多时，则使用较小的交叉概率，以免较好的个体被很快地破坏掉。

6）变异操作

通常，变异操作是以较小的概率将某些个体的某些位简单、随机地变成其他值［7］。本文结合布线问题的特点，借鉴了免疫遗传算法［8］中接种疫苗的思想，使变异操作不是对某些基因位进行随机盲目地修改，而是使这些基因位的修改更有可能产生出适配度更高的个体。其具体实现与产生初始种群时的改进方法相似，将随机选定的发生变异的基因位的值（对应于某根电缆的布放方案）按概率修改为值i，即：

式中，n为当前电缆的候选路径数目；i为候选路径编号，i＝0，1，…，n－1。

也就是说，通过变异使某根电缆的布放方案以较大的概率变为选择长度更短的路径，而不是完全随机地换成其他路径。通过这种改进的变异方法，不仅可以达到通常通过变异加大种群多样性的目的，而且可以达到接种疫苗、提高后代个体适应度的效果。另外，将变异概率设计成随种群中符合约束条件的个体数目的多少而变化。

7）检测操作

传统的遗传算法并没有这一操作，这是本文的另一项改进，目的是防止在交叉、变异的过程中出现退化现象。该操作借鉴了De Jong的“杰出人才模型”［9］及免疫遗传算法中免疫检测的思想。具体方法是对经过交叉、变异后的新一代个体进行检测，如果其最佳个体反不如上一代最佳个体的适应度高，那么就复制上一代的最佳个体取代新一代个体中适应度较低的某一个体。

8）确定算法终止条件

由于最大进化代数很难进行合适的设置，为适应算法性能的动态变化，较好地兼顾算法的优化性能和时间性能，可采用佱阈值法设计算法的终止条件［10］，即若最优解经过连续若干代（本文设为100）进化仍保持不变，则终止搜索过程。

5 仿真结果

5.1 实例计算

图2表示一个6结点8通道的简单电缆通道网络，其中括号内的数字为各段通道的编号，括号外的数字为各段通道的长度，即通道段长度矩阵L＝［3，3，1，2，5，5，2，3］。

假设要在图2中每两个结点间都布1根电缆，电缆可走任意路径，但要符合各段通道的容量约束要求。由于该图是无向图，全连接时最多存在N·（N－1）／2（N为结点数）条链路，故共需布放15根电缆。已知每段通道的最大容量均为20，即通道段容量矩阵：

Q＝［20，20，20，20，20，20，20，20］T

图2 电缆通道网络图

所有电缆的基础信息如表2所示。

表2 电缆基础信息

在实际操作时，通常要首先搜索出每根电缆的全部可行路径，但在进行全局优化时，并不一定要把所有的可达路径都列为候选路径，因为有些路径在实际中根本不可能被选中，例如连接结点A和B的电缆，虽然存在路径A→E→C→D→F→B，但这种路径并没有多大实际意义。另外，在有些情况下，用户可能需要为某些电缆指定特殊的布线规则，例如要求连接结点A和D的电缆必须经过（或禁止经过）结点B。所以在选择候选路径时，可以指定一个候选路径数目，例如每根电缆都只自动搜索长度最短的两条路径作为该电缆的候选路径，或者先给出某根电缆的所有可达路径，然后由用户指定几条路径作为候选路径。在本文中，为了测试算法的最终性能，将所有可达路径都作为候选路径以增加搜索难度。

采用上述构造的改进遗传算法对该例求解，计算结果如下（详见表3、表4）：

优化变量：

X∈｛（0，0，0，0，0，0，0，0，0，0，0，0，0，0，0），（0，0，0，0，0，0，0，0，0，0，0，0，0，1，0）｝；

最小费用：

C＝216

实例计算结果表明本算法能够快速、准确地找到全局最优的电缆布放方案，证明了该算法对求解电缆布局优化问题是可行、有效的。

5.2 性能分析

针对上述实例，应用传统遗传算法和改进遗传算法分别求解。两种算法都基于C语言编程并在同一台计算机上运行，其中种群规模和终止代数（即最优解连续出现代数）均设为100。两种算法各随机运行20次，其测试结果如表5所示。

表3 电缆最优布放方案所需费用

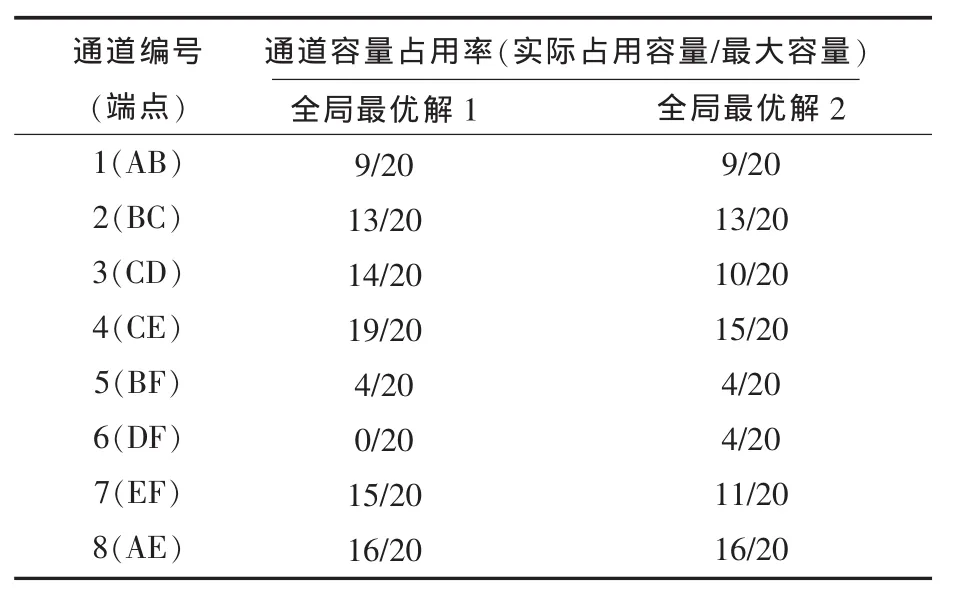
表4 电缆最优布放方案所需容量

表5 两种算法性能测试结果

从表5可以看出，与传统遗传算法相比，应用改进遗传算法能够在获得相同最优解 （即最小目标值）的同时大大减少迭代次数，计算时间也相应减少。若将某些关键通道的最大容量减小，如：

Q＝［15，20，20，20，10，20，20，15］T

则这种收敛速度的差距还将更大，而且传统算法还常会出现收敛于某些局部最优解的情况。另外，随着电缆通道网络中结点数量的增加，本算法的优势还将更加明显。

6 结束语

本文采用遗传算法进行船舶电缆布局优化设计，具有很高的实用性，使得船舶设计中复杂的布线工作实现自动化和最优化，以达到提高效率与降低成本的目的。与传统遗传方法不同的是，本文对产生初始种群的方法、选择算子及变异算子进行了改进，并增加了检测操作，大大提高了算法的收敛速度和准确性，而且避免了传统算法容易陷入局部最优的不足。当然，该方法还有许多值得进一步研究的地方，例如在数学建模时可以考虑更多的实际因素，使其具有更强的适用性，另外仍需不断提高算法自身的寻优能力，以更好地发挥其优越性。

［1］杨新敏，孙静怡，钱育渝.城市交通流配流问题的遗传算法求解［J］.昆明理工大学学报（理工版），2002，27（5）：144－146.

［2］HOLLAND J H.Genetic algorithms and the optimal allocations of trials［J］.SIAM Journal of Computing，1973（2）：88－105.

［3］HOLLAND J H.Adaptation in natural and artificial systems［M］.Ann Arbor，MI：The University of Michigan Press，1975.

［4］钱志勤，滕弘飞，孙治国.人机交互的遗传算法及其在约束布局优化中的应用［J］.计算机学报，2001，24（5）：553－559.

［5］BAKER J E.Adaptive selection methods for genetic algorithms ［C］／／Proceedings of the First International Conference on Genetic Algorithms and Their Applications. Hillsdale：New Jersey，1985.

［6］WHITLEY D，et al.The GENITOR algorithm and selection pressure：why rank base allocation reproduction trials is best［C］／／Proceedings of the 3rd International Conference on Genetic Algorithms.LosAltos：Morgan Kaufmann Publishers，1989.

［7］姚文俊.遗传算法及其研究进展［J］.计算机与数字工程，2004，32（4）：41－43.

［8］王小平，曹立明.遗传算法——理沦、应用与软件实现［M］.西安：西安交通大学出版社，2004.

［9］李敏强，寇纪凇，林丹，等.遗传算法的基本理论与应用［M］.北京：科学出版社，2002.

［10］王凌.智能优化算法及其应用［M］.北京：清华大学出版社，2001.

The Application of Genetic Algorithm in Optimal Design for Ship Cable Routing

Wang Xue-lian Huang Jun
China Ship Development and Design Center，Wuhan 430064，China

Local optimization on cable layout is a technical obstacle to achieve automatic cabling in ships.The solution to this problem can save both time and cost dramatically so that the technology is significant.This paper establishes the optimizing model on cable routing problem.On the basis of analyzing the weakness of traditional genetic algorithm，the paper builds an improved genetic algorithm which improves population initialization，selection and mutation operator，and adds detection operator.The simulation results show that this genetic algorithm is a method of routing optimization which has the global optimum seeking ability.At the same time，the method has high efficiency and practicability，and can be extended to solve other optimization problems concerning ship design.

genetic algorithm；optimum design；cable laying；ship

U665

A

1673－3185（2009）04－72－04

2008－11－12

汪雪莲（1978－），女，工程师，硕士。研究方向：船舶优化设计。E-mail：lily1128＠126.com

黄 君（1980-），男，工程师，硕士。研究方向：船舶系统设计