舰船典型节点参数化建模及形状优化

冯国庆 任慧龙 李巧彦 李 辉

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

舰船典型节点参数化建模及形状优化

冯国庆 任慧龙 李巧彦 李 辉

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

给出一种船舶结构典型节点的参数化建模及形状优化方法，利用APDL建立某典型节点参数化模型的方法，将该节点形状参数定为设计变量，节点的应力集中系数作为优化设计的目标函数。通过不断改变形状参数，找出较小的应力集中系数。结果表明，该方法可有效降低应力集中，为舰船典型节点结构设计和优化提供参考。

参数化建模；APDL；应力集中；形状优化

1 引言

船舶结构设计中，往往会有减小应力集中系数的要求，特别是针对疲劳强度问题，降低节点的应力集中系数，可有效地提高节点的疲劳寿命［1］。为了降低节点的应力集中系数，工程上采用了很多种方法，一般可通过改变节点形状（过渡肘板形状）达到这一目的。本文针对船体上的典型节点，利用参数化建模方法，将节点形状参数定为设计变量，节点的应力集中系数K则作为优化设计的目标函数。通过不断改变形状参数，可找出较小的应力集中系数。

2 节点结构参数化建模

本文所选的节点是船体典型节点之一，为T形纵骨穿过非水密舱壁板处节点，如图1所示。该结构的各构件几何尺寸：船底板2 600×400× 14.5（mm）；非水密舱壁板1 200×400×14（mm）；穿过舱壁板的T形纵骨12×300／20×90（mm）；舱壁板上的垂向加强筋150×12（mm）；开孔处的两块补板，开孔的圆角半径取为25 mm，补板下沿距底板高度取为e＝50 mm，补板上沿距纵骨面板为c＝0.2腹板高，补板与舱壁板搭接宽度为50 mm；无折边肘板的初始值为12×200×200（mm），两角处削宽20 mm。

图1 纵骨截面图

2.1 参数定义

用APDL语言实现参数化建模的过程，首先要定义各个尺寸参数。参数可以在建模过程中的任何部分定义，它们将会在建模过程中被使用。下面介绍参数化建立节点模型时所定义的部分参数［2］。

1）T型纵骨腹板高度

T型纵骨腹板的建造高度是300 mm，这意味着在ANSYS中采用板单元建模时，必须考虑每个翼板厚度的1／2，所以，模型上下翼板板单元间的距离就是317.25 mm。参数设定如下：

*SET，h1，0.3＋T1／2＋T3／2！纵骨腹板的模型高度

2）肘板椭圆线定义

肘板采用的是一段椭圆线，见图2。令椭圆中心坐标（Z，Y），椭圆上两点坐标A（ZZ1，YY1），B（ZZ2，YY2）。椭圆长边长度为a，短边长度为b，由椭圆方程易知：

选用Y，Z，YY1，ZZ1，YY2，ZZ 2来表示椭圆方程参数a，b，可减少后面节点优化的设计变量，提高优化效率和精度。

在APDL中定义设定椭圆参数方法如下：

a＝SQRT （（（ZZ1－Z）**2* （YY2－Y）**2－（ZZ2－Z）**2* （YY1－Y）**2）／（（YY2－Y）**2－（YY1－Y）**2））！椭圆的长半轴

b＝SQRT （（（ZZ1－Z）**2* （YY2－Y）**2－（ZZ2－Z）**2* （YY1－Y）**2）／（（ZZ1－Z）**2－（ZZ2－Z）**2）） ！椭圆的短半轴

2.2 几何模型参数化生成

定义了参数后，就要在建模过程中调用参数，实现参数化建模的目的。值得注意的是，建模的过程必须在PREP7前处理器中完成。肘板曲线参数化建模主要语句如下：

／PREP7 ！进入前处理器

K，，，yy1，zz1 ！用由参数表示的坐标（0，yy1，zz1）来建立关键点，点号缺省，则将当前最小标号赋给新建点

K，，，yy2，zz2 ！建立坐标为（0，yy2，zz2）的关键点

WPOFF，0，Y，Z ！将工作平面坐标偏移到椭圆中心点

WPROT，0，0，90 ！再将工作平面绕X轴旋转90°

CSWPLA，11，1，RATIO，，！根据当前定义的工作平面的圆点定义局部坐标系，该坐标系的标号为11，是椭圆坐标系，由参数RATIO控制椭圆形状。

L，45，48 ！在局部坐标系下由两点45，48建立线，即为椭圆的一部分。

图2 肘板曲线各参数示意图

2.3 参数化网格划分的实现

1）单元类型及材料属性

在划分网格之前首先要定义单元类型，在本模型中所选单元均为 SHELL63弹性板单元。ANSYS中板厚是通过实常数定义，定义方法为：

T1＝0.0145 ！设定厚度参数

R，1，T1，T1，T1，T1，0，0！为板单元定义实常数1，板厚是T1

节点结构材料为钢材，属于各向同性的线弹性材料，其性能参数定义：

MP，EX，1，2.06e11 ！定义材料的杨氏模量为2.06e11

MP，PRXY，1，0.3 ！定义材料的泊松比为0.3

2）网格划分［3］

网格数量的多少将影响计算结果的精度和计算规模的大小。一般来讲，网格数量增加，计算精度会有所提高，但同时计算规模也会增加，因此在确定网格数量时应权衡这两方面因素综合考虑。兼顾这两方面的要求后，本模型在应力变化梯度比较大的肘板端部与纵骨面板相接的区域，单独划出一小块面积，实施细网格划分。为了便于在计算应力集中系数时提取应力，划分的细网格单元边长取为腹板厚度的1／4。考虑到网格数量过多，消耗机时大，在应力分布相对较平稳的其它区域，采用了稍粗的网格，边长取为20 mm。

参数化网格划分主要命令如下：

LESIZE，77，T2／4！ 定义线号是77的线的单元大小为T2／4

REAL，1 ！指定单元实常数，在下面生成的单元将默认使用该实常数

ASEL，S，LOC，Y，0 ！选择y坐标为0处的面

AESIZE，ALL，EL ！划分的面单元边长由参数EL决定，这是控制单元大小的一种方法

AMESH，ALL ！用自由网格划分所选集合内的面

当把一个面的边线都用LESIZE命令划分好线单元的大小后，再用AMESH划分该面时，在边线处还是会按照线单元的大小来划网格。所以，要想很好地控制一个面的网格大小，有时要先划分它的边线。本模型中，在应力变化梯度大的肘板和面板相接处专门建立的一小块面积的网格大小就是用这种方法来控制的。事实证明，用这种方法划出的网格还是比较均匀的（图3）。

图3 结构细节局部细网格

2.4 参数化加载的实现

对于该节点结构，边界条件为纵骨一端完全刚性固定，在另一端面内，限制5个方向的自由度，即将该面建成刚性面。

1）求该截面形心位置，以便提取位于此处的节点，施加刚性约束和集中载荷。形心坐标公式如下：

2）用APDL语言的NSEL命令分别选取Z＝1 500 mm截面上的所有节点及形心附近的节点，用CERIG命令把截面上所有节点以形心附近节点为基点建立刚性约束。

3）用F命令在形心节点上施加沿Z向的集中载荷。

4）对于位移边界条件，直接选取纵骨两端截面用D命令施加。节点有限元模型载荷及边界条件见图4。

图4 有限元模型的载荷及边界条件

以上操作的主要命令流如下：

NSEL，S，LOC，Z，1.5 ！选择Z坐标是1.5的面内的所有节点

NSEL，R，LOC，Y，H0－EL／2－0.002，H0＋EL／2＋0.002！在所选集合里面再选Y坐标在H0－EL／2－0.002和H0＋EL／2＋0.002之间的节点。

＊GET，N0，NODE，0，NUM，MAX ！ 提取所选节点集合中节点的最大编号，并赋值给参数N0

NSEL，S，LOC，Z，－0.9 ！重新选取新的节点集合，Z坐标是－0.9的面内的所有节点

D，ALL，ALL，0，，，， ！对该集合中的节点约束所有六个方向的自由度

NSEL，S，LOC，Z，1.5 ！重新选取新的节点集合，Z坐标是1.5的面内的所有节点

D，ALL，UX，0，，，，UY，ROTX，ROTY，ROTZ！对该集合中的节点约束所有五个方向UX，UY，ROTX，ROTY，ROTZ的自由度

CERIG，N0，ALL，UZ，，，，！将集合中所有节点以节点N0为基点，建立的刚性约束

F，N0，FZ，F ！对节点N0施以z向合力F

2.5参数化提取结果的实现

1）应力提取

节点参数化建模完成后，用以下命令就可以完成分析计算：

／SOLU ！进入求解器

SOLVE ！开始求解计算

FINISH ！计算结束，退出求解器

模型计算结束后，提取应力、查看结果都要在后处理器中进行。后处理器有通用后处理器POST1和时间历程后处理器POST26两种，POST1用于分析整个模型在某个载荷步的某个子步、或者某个结果序列、或者某特定时间或频率下的结果。前面节点计算分析后结果应力云图（图5）。

图5 结构细节应力云图

参数化提取结果的部分主要命令：

／POST1 ！进入通用后处理器

NSEL，S，LOC，X，0

NSEL，R，LOC，Y，

NSEL，R，LOC，Z，B2＋X1＋T2／4－0.0002，B2＋X1＋T2／4＋0.0002 ！按坐标（0，H1，B2＋X1＋T2／4）选取第一个节点。

NSORT，S，1 ！将所选节点按照最大主应力S1来排序

*GET，S11，SORT，，MAX ！在排好序的节点集合里，提取最大的主应力，并赋值给参数S11

*GET，N1，SORT，，IMAX ！提取主应力最大的节点号，并赋值给参数N1

2）应力计算方法［4］

在焊缝附近受力构件的表面上选取4个有限元节点（图6），插值点处的最大主应力应根据所选有限元节点处的最大主应力用拉格朗日插值法求得。但插值点应位于4个有限元节点之间。最大主应力应按下式计算：

式中，σ1为有限元节点1处的最大主应力；σ2为有限元节点2处的最大主应力；σ3为有限元节点3处的最大主应力；σ4为有限元节点4处的最大主应力；C1、C2、C3和C4为系数，应按下列各式计算：

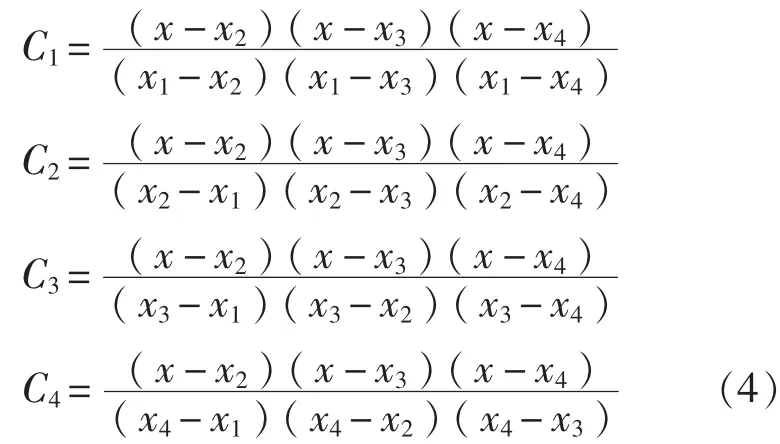
式中，x为插值点距焊趾的距离；x1为有限元节点1距焊趾的距离；x2为有限元节点2距焊趾的距离；x3为有限元节点3距焊趾的距离；x4为有限元节点4距焊趾的距离。

图6 应力插值示意图

应力σh应按下式计算：

式中，σt／2为按式（3）计算的距焊趾t／2处的最大主应力；σ3t／2为按式（3）计算的距焊趾3t／2处的最大主应力；t为板厚。

3 形状优化

3.1 基于APDL的节点形状优化过程

1）生成分析文件

分析文件生成是ANSYS优化设计过程中的关键部分。ANSYS程序运用分析文件构造循环文件，进行循环分析。在分析文件中，模型的建立必须是参数化的（通常是优化变量为参数），结果也必须用参数来提取 （用于状态变量和目标函数）。优化设计［5］中只能使用数值参数。前面已经完成了节点参数化建模，把整个过程的命令流连起来存在一个文件里，如保存在名为NODEOPT.LGW的文件中，就可以作为优化的分析文件了。

2）进入优化处理器OPT，指定分析文件

／OPT

OPANL，NODEOPT，LGW

3）声明优化变量

节点形状优化过程中，可选用的设计变量很多。然而设计变量越多的需要迭代次数越多，从而需要更多的机时。所以应该尽量减少优化变量数目，在本结构模型中，参数化建模的各个参数都可以作为设计变量，通过把椭圆方程参数a，b用参数YYY、ZZZ、X1和X2来表示，对设计变量进行合并。这样，设计变量缩减为肘板曲线的椭圆中心的相对坐标值YYY和ZZZ以及肘板的两边长X1和X2。设计变量X1，X2（肘板的两边长）的变化范围是参照相关规范而定的。对于椭圆中心的相对坐标值YYY和ZZZ，考虑建造和工艺的要求，肘板曲线必须是1／4椭圆上的一部分，因此YYY和ZZZ要大于等于0；而上限则考虑椭圆中心离肘板越远，椭圆越大，这样肘板曲线就趋近直线，导致目标函数K增大，显然不是优化收敛的方向，因此上限不必取得太大，否则会无谓地增大优化的搜索空间，从而影响优化效率。

以下是针对本结构模型的主要命令流：

OPVAR，K，OBJ，，，5E－6 ！目标函数

OPVAR，YYY，DV，，1.0，0.005 ！设计变量

……

4）选择优化方法及循环控制

ANSY提供了两种优化方法：零阶方法和一阶方法。这里选用一阶方法。设定优化方法的命令流如下：

OPSAVE，NODEOPT，OPT！将所有的优化数据写入名为NODEOPT.OPT的文件中，以便查看

OPKEEP，ON ！存储最佳序列

OPTYPE，FIRST ！指明优化方法为一阶方法

OPFRST，100 ！最大循环次数，超过这个次数，循环会中止

5）执行分析察看分析结果

完成以上步骤，就可以开始进行优化分析，命令流为：

OPEXE ！执行优化

分析完成后，用命令

oplist，all

列表显示所有的设计序列，查看优化变量随迭代过程变化；或者用图显示指定参数随序列号的变化。

3.2 优化设计计算的结果及分析

1）优化设计结果

图7和图8分别是优化过程中应力集中系数K随迭代序列号和肘板曲线椭圆中心相对坐标YYY的变化曲线。

图7 K－Set number关系曲线

表1 优化前后的优化变量和参数值

图9 优化前后的肘板形状

结果表明，优化后节点结构的应力集中系数K减小了4.6%；同时，虽然没有刻意追求肘板的面积，但优化后肘板的面积却大幅度减小65.10%，比优化前节省材料，降低成本。

2）优化设计结果的分析

首先，从最优参数序列来看，优化以后肘板曲线的形状接近圆形，而且，椭圆的尺度也接近搜索域中最小值，这说明该曲线的曲率增大对应力集中系数的减小是有利的。

第二，肘板的边长也接近设计变化范围中的最小值0.12 m。为了考察肘板底边长X1对于K的影响，作者又计算了当X1＝0.2 m，而其他设计变量值均不变（同第19序列）时的节点集中应力系数，得K＝1.383 5。与优化结果K＝1.387 5十分接近，相差不足0.3%。这说明K对肘板的边长并不敏感。为了提高优化效率，可以考虑将对目标函数影响不明显的设计变量删掉，再进行优化，这是后续工作。

第三，关于网格精度对结果的影响。其一，单元多少影响到加载后计算出的节点应力值；其二，计算K时提取的4个有限元节点的位置及应力值对该处的网格密度 （或者说单元边长）较为敏感。鉴于这两个原因，网格划分的不同，计算的结果肯定有差异。前面已经详细论述了网格疏密和数量的确定原则，综合考虑了在应力变化急剧的地方网格能够反映出应力的变化规律，以及网格数量不能过大两方面的因素后，采用了疏密不同的网格方案。为了寻求更好的方案，特在粗细网格之间进行网格过渡，如图10，计算出应力集中系数比没有过渡网格时降低了1.0%，这为寻求更加稳定合理的结果，提供了又一个努力方向。

第四，肘板曲线采用椭圆线，主要是出于方便加工制造的考虑。当然，采用样条曲线可能会优化出更好的结果，这也是节点优化的后续工作之一。

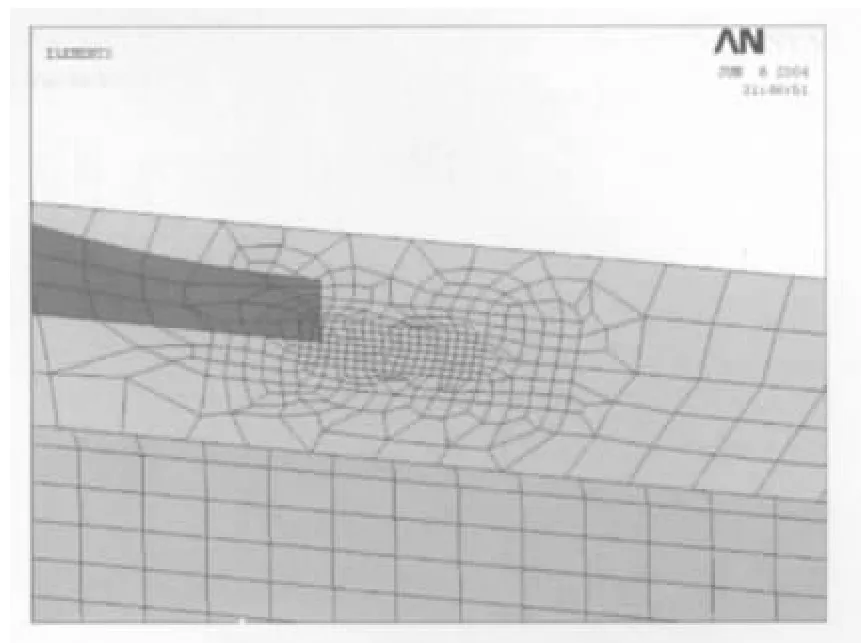
图10 网格过渡

4 结论

ANSYS的APDL语言为结构的模型化提供了良好的接口工具，可以利用APDL语言方便地实现结构的参数化建模。利用APDL建立典型节点参数化模型，并将该节点形状参数定为设计变量，节点的应力集中系数作为优化设计的目标函数。通过不断改变形状参数，能够找出较小的应力集中系数。结果表明，基于参数化建模的优化方法可以有效解决结构的优化工作，为舰船典型节点结构设计和优化提供参考。

［1］冯国庆.船舶结构疲劳评估方法研究 ［D］.哈尔滨工程大学博士学位论文，2007.

［2］博弈创作室.APDL参数化有限元分析技术及其应用实例［M］.北京：中国水利水电出版社，2004.

［3］施丽娟，崔维成.集装箱船舱口角隅应力集中系数的有限元分析的精度［J］.中国造船，2003，44（1）：31-38

［4］中国船级社，船体结构疲劳强度指南［S］.北京：人民交通出版社，2001.

［5］任慧龙，冯国庆，娜日萨.船舶甲板横梁翼板和腹板开口形状优化设计 ［C］／／ANSYS中国用户年会论文集，2002.

Parametric Modeling and Shape Optimization of the Typical Structural Details of Ships

Feng Guo－qing Ren Hui－long Li Qiao－yan Li Hui
College of shipbuilding engineering，Harbin Engineering University，Harbin 150001，China

A parametric modeling and shape optimization method of a typical structural detail of warship is presented in this paper.First，a parametric model of a typical structural detail of warship is built by APDL.Then，the shape parameters of the structural detail are defined as design variables and the stress concentration factor of the structural detail is defined as the objective function of the optimization design.By changing shape parameters，a relatively small stress concentration factor is obtained.The results show that stress concentration can be effectively decreased using this method.This method can offer reference in the design and optimization of typical structural details of warships.

parametric modeling；APDL；stress concentration；shape optimization

U661.42

A

1673－3185（2009）04－28－06

2008－04－08

冯国庆（1976－），男，博士，讲师。研究方向：船舶与海洋工程环境载荷预报及结构强度评估。E-mail：fengguoqing＠hrbeu.edu.cn

任慧龙（1965-），男，教授，博士生导师。研究方向：船舶与海洋工程环境载荷预报及结构强度评估