半潜船概率破舱稳性浅析

郝威巍 宗 智，2 林 哲 陈 伟

1大连理工大学船舶工程学院，辽宁大连116024 2工业装备结构分析国家重点实验室，辽宁 大连116024

半潜船概率破舱稳性浅析

郝威巍1宗 智1，2林 哲1陈 伟1

1大连理工大学船舶工程学院，辽宁大连116024 2工业装备结构分析国家重点实验室，辽宁 大连116024

应用国际通用的概率破舱稳性理论对半潜船的分舱情况和破舱稳性进行初步分析。通过大量计算研究舱室垂向水平分隔限制、初始装载状态和边舱几何形状对分舱指数A的关系及影响，得到相关要素间的关系曲线图表和船舶设计指导原则。结合一艘半潜船破舱稳性概率方法的计算实例，针对概率衡准（SOLAS）做出计算结果的理论解释。最后给出半潜船的设计要素，对船舶设计初期指导压载水舱划分和评价概率破舱稳性具有参考价值。

新船型；半潜船；破舱稳性

1 引言

随着能源、经济、通信事业等在全球范围的深入发展，半潜船的营运市场日益扩大。随着各国对海洋石油开发力度的加大，各工程船，诸如无动力系统的海洋平台等的快速移动，成为海洋石油开发进程的关键环节。如今，半潜船的发展可以将海洋工程结构物安全快速、平稳送达指定海域，从而达到移动钻井平台的目的［1］。另外，目前世界大多数海洋石油钻井平台正处于保修期，需用半潜船将它们运送到船厂。同时全球通信业的迅猛发展，提供了海底光纤电缆等大量铺设的工作，由于拥有半潜特性，半潜船可以更方便地执行铺设任务。据统计，有动力且能远航的半潜船全世界仅有30多艘，因此对半潜船新船需求量很大。

半潜船属高技术含量、高附加值船舶，世界上为数不多，国内相对缺少母型船作技术参考，部分船东、船检以及海事局对于此类船舶也缺少实际经验。为此，结合一艘半潜船的改装设计，本文对半潜船的破舱稳性做专门的探讨，为半潜船的设计提供更加合理和可靠的技术支撑。

2 破舱稳性概述

在正常航行时，半潜船的货物是放在甲板上的，而不是在舱内。因此，半潜船主要的舱室几乎都是压载舱。同时，为了方便压载水的调整，半潜船一般设置很多舱室。比如，我国第一艘半潜船，其压载水舱有40多个。众多的压载水舱给破舱稳性的计算带来了很大的困难。根据目前的SOLAS规定，破舱稳性的核心是计算不同舱室以及它们不同组合发生破坏时的稳性［2］。随着压载水舱的增多，可能的破损组合数成指数增加，破舱稳性的计算就越困难。

破舱稳性计算的最终目的是得到一定载况下的稳性曲线，从而对船舶稳性进行评价。其计算过程可归纳如图1所示。

图1 破舱稳性计算过程

目前，国际上尚无针对半潜船的规范约定，半潜船的载货特性决定了其属于目前ICLL66规范中的B型货船，按SOLAS规范，该类型船舶的破舱稳性应采用概率方法进行校核计算。航行状态下的半潜船情况和常规船舶有相似之处，如可能受到风浪流、礁石、碰撞等造成船舶破损的情况。对于作业状态，设计要求就是在平静海况下进行货物的装载，所以船舶破损情况概率较低，但本文仍给出此状态下的概率破舱稳性，旨在探讨半潜船的稳性特质，以及现有规范所设定参数对其所产生的影响。

船舶破损稳性的基本问题是船舶破损后浮态的确定。按损失浮力法，浮态及稳性计算采用“自由纵倾”方式，也就是三维方法确定船的总复原力臂，即重力作用线与浮力作用线之间的水平距离。传统的复原力臂是这个水平距离在船体横剖面方向的投影，没考虑纵倾对稳性臂的影响。

3 半潜船的航行破舱稳性

3.1 要求指数R和船舶所能达到的指数A

概率方法是基于大量海损统计资料得到的，实际上是进行一种分布函数的计算。实际上，船舶在航行作业中破损的位置是相当随机的，但知道破损位置就可以求得该处破损后船舶的稳性即破舱稳性。概率方法就是求出船舶某处破损的概率乘以该处破损后船舶生存的概率的集合——达到的分舱指数A，与最低分舱标准——要求的指数R作比较。对于计算数据，BV建议使用五位小数计算，最终结果用至少三位小数计算。

船舶所要求的指数R公式表示为：

对于Ls（m）超过100 m的船舶

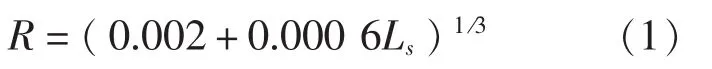
对于Ls（m）超过80 m，但不超过100 m的船舶

式中，R0为式（1）算出的R值。

船舶所能达到的分舱指数A公式表示为：

式中，i表示所考虑的每一个舱或舱组；Ls为船舶处于最深分舱载重线时限制垂向浸水范围的甲板及其以下部分最大投影型长度，即船舶分舱长度；pi表示所考虑的舱或舱组可能浸水的概率，不考虑任何水平分隔；si表示所考虑的舱或舱组浸水后生存概率，包括任何水平分隔的影响。

需要指出的是，计算A时采用的是无纵倾平浮状态，且其计算仅包括有助于增加达到的分舱指数A值的浸水情况——整船长范围内涉及单个舱或多个相邻舱的所有浸水情况，包括边舱浸水情况［3］。这也是随着舱室增多破舱稳性计算成指数增长的主要原因。

在正式计算之前，需要对规范要求的两种船舶吃水状态：即最深分舱载重线状态和部分载重线状态进行加权计算，前者是指核定的船舶夏季吃水，即航行时的设计吃水状态；后者是指空船吃水加上空船吃水与最深分舱载重线之间差值的60%的吃水状态。求得了上述两种载况下船舶破损后能够生存的概率sl和sp，就可以根据所考虑的吃水，对每一舱或舱组的si按下式计算：

式中，sl为在最深分舱载重线处的s因数；sp为在部分载重线处的s因数。

破舱稳性的计算是以舱组为单元的，舱组的概念是以SOLAS公约中对船舶破损范围的限制为基础，并按相邻两道有效水密舱壁划分舱组。IMO.A534中关于破舱稳性规范有如下要求，相邻两道有效水密舱壁是指满足相邻两道水密舱壁的间距大于1／3L2／3或14.5 m取小者。不满足距离要求时为了满足舱壁间最小间距的要求，相邻两道水密舱壁之间的一道或两道应视为无效，破损时考虑相邻两舱同时破损。舱组划分完成后即可进行纵向、横向和垂向三维破损范围的确定。

普通船舶的破损范围没有异议，但是半潜船由于货物甲板的特殊性需要对破损的垂向范围展开讨论。

3.2 水平分隔对残存概率的影响

对于航行状态的半潜船，水线在货物甲板之下，与普通船舶无异，但用于提高强度而增设的垂向分布的多层水平甲板将对破损范围产生一定的限制，从而对半潜船所能达到的指数产生影响［4］。对水平分隔以下的舱或舱组，其s值应乘以该水平分隔以上处所不浸水的概率的缩减因数νi求得。对于水平分隔以上处所同时浸水能使指数A增加一个正值的情况，该舱室或舱组的s值应在s基础上加上一个因同时浸水得到的s值乘以因数（1－ν）求得的值。

水线以上设有水平分隔时概率因数νi应按下式计算：

式中，H为受Hmax限制的一个高度，m；Hmax为在基线以上最大可能的垂向破损范围，m；或Hmax＝，如Ls≤250 m或Hmax＝d＋ 7，如Ls＞250 m，取小者。当假定的破损范围的最上层水平分隔是在Hmax以下时，νi＝1。

该式说明吃水对于概率因数νi起着决定性作用，Hmax并不是船舶的型深D，而是一个统计公式得到的值，通常比D小。νi所反映的垂向破损范围假定分布函数如图2所示。

图2 垂向破损范围的假定分布函数

在规定破损范围之后需要对划分的舱组进行组内和组间的所有可能的破损舱室组合。半潜船主要是压载水舱间的组合，包括主、辅压载舱室，对于存在多层甲板的船舶其组合情况更多［5］。

明确了舱组间的破损组合就可以进行概率方法破舱稳性最耗时的工作——船舶能达到的分舱指数A的计算。如公式（1）所示，这一部分的计算包括船舶可能浸水的概率pi和浸水后的生存概率si。

3.3 概率因数pi

可能浸水的概率因数pi主要由Ls的后端点到所考虑的舱室后端最前部位、前端最后部位的距离决定，并受到某一边舱和其相邻的内侧舱室同时浸水的情况的缩减影响。技术细节在于舱室横向分隔的考虑，以及纵向限界之间平均横向距离的量取。前者不仅考虑把Ls分隔成各破损区域的已有横舱壁，也考虑单独的较小局部水密舱室浸水对破舱稳性的影响。计入局部分舱的考虑虽然会使计算量增大 （因为需要做更多的舱室组合和破损概率计算），但是这样处理的好处是得到一个大于 （或至少等于）不计局部分舱时的分舱指数。后者的量取较为繁杂，对于破损区域内含有宽度突变的情况则需要对该区域进行划分，每个区域内距离的量取应在最深分舱载重线处由船壳板至与纵舱壁平行的平面之间在水平面上向中心线垂直量取。由于半潜船的舱室在载货区多为压载水舱，舱室的构成相对整齐，所以计算耗时相对较少。这一部分的计算包括一舱和多舱计算，对于3个或更多相邻舱室为一组的舱组，如果该舱组的无因次长度减去该舱组最前和最后舱室的无因次长度大于Jmax，则其因数pi等于0。因数pi的形成如图3所示。

3.4 残存概率s

在概率方法的破舱稳性计算中，分舱指数A的计算最耗时的地方在于浸水后生存概率s的计算。

通常对任一初始装载情况的任一浸水情况的生存概率s应按下式计算：

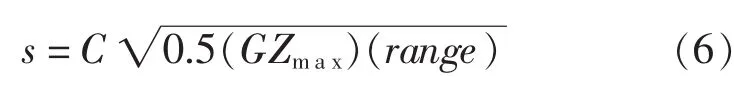
式中，C＝1，如θe≤25°；C＝0，如θe＞30°，C＝，其他情况；GZmax为以下（range）所给的最大正复原力臂（m），但不大于0.1 m；range为超出平衡角的正复原力臂的范围 （°），但不大于20°；但是此范围应在不能被风雨密门关闭的开口被淹没的角度处终止。θe为最终横倾平衡角（°）。

从公式可以看出，生存概率s主要依赖于最终横倾平衡角θe这个变量。这一变量是通过模拟船舶进水后的浮态获得的，与船舶的吃水（即之前所述的载况）及进水点密切相关。船舶倾斜时，自身将找到位能为最小值的位置，从而消耗在倾斜船舶的功取得最小值。船舶的这种倾斜状态被称为“自由漂浮”或“自由纵倾”，该状态下的稳性曲线计算称为“自由纵倾稳性计算”或“最小稳性计算”。计算表明，吃水较大时生存概率s的数值普遍降低，这是由于大吃水下，船舶剩余干舷减少，水线离船舶的空气管、通风筒、风雨密门或舱口盖关闭的开口距离减少，稍有风浪作用及较小的横倾角也会引起相关舱室的累积进水，从而增加船舶进水的舱室，也就恶化了船舶破损后的剩余稳性［6］。生存概率s还与诸如进水角、复原力臂、稳性正值范围等剩余稳性有关。计算残存概率如图4所示。

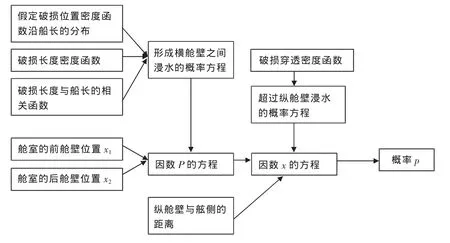
图3 因数pi的形成

图4 计算残存概率的示意图

需要指出的是，式（6）中GZmax对生存概率s的影响也是举足轻重的。对于部分吃水的载况，由于水线面面积相对较小，进水后船舶稳性较差，补救措施是增加排水量以达到增加水线面面积的效果。一旦船舶发生破损，可以用自由液面较小的边舱进行调节［7］。如果用双层底的压载舱进行调节，会导致较大的自由液面，从而对GM产生较大的修正，得不到较大的GZmax值。增加的压载水也会带来相应问题，首先自由液面的修正会降低船舶的复原力臂，而且随着压载水的增加，排水量也增加，KG值在下降，储备浮力也跟着减少。

在计算中，所选取的载况相应的参数，诸如该吃水下的GM值是需要手动输入的，这意味着可以在一定范围内找到最佳的GM值，也就是破舱情况的极限重心曲线问题。最佳GM值可以得到较好的破舱稳性的计算结果（得到最佳的GZmax）。因为GM、KG满足关系式

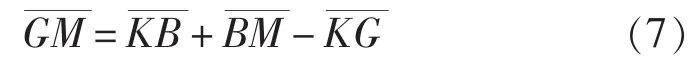
式中，KB为浮心高度；BM为初稳心半径；KG为船舶重心高度。

增加压载水⇒KG↑⇒GM↓⇒WB↑⇒KG↓DIS↑⇒GM↑。

不同船舶有不同的特性，需要wdt针对性的破舱控制计算，是否能找到指导性的控制方法是个值得深入讨论的问题［8］。

上文对概率方法求解船舶破舱稳性做了基本陈述，需要指出的是不同机构对舱室渗透率的定义不同。半潜船的多数舱室为压载水舱，对于压载状态不佳需要载固体压载的半潜船，其舱室的渗透率有待进一步讨论。

4 半潜船的作业破舱稳性

虽然作业状态工作环境相对安全，但为了讨论半潜船的破舱稳性及其特殊性 （上升下潜过程中，船舶中部的货物甲板将完全沉入水中），本文也对作业状态下的半潜船进行讨论并给出与航行状态的结果对比。作业破舱稳性的计算流程与航行状态基本相同，但具体参数的选取不大相同。

对于基本载况的选取，最深分舱载重线情况取的是船舶能够下潜的最大深度。由于舱室功能结构没有变化，舱组的划分同航行状态。可能浸水的概率pi与航行状态无异，关键是浸水后生存概率s的计算［9］。

由于作业升沉时水面没过货物甲板，这一区域内的水平分隔对s的影响不计，即νi＝1。由于作业时吃水较大，船舶处于非常危险的平衡状态，操作稍有不慎，即可造成船舶的倾覆，一旦发生破损，浸水后的生存概率s很不乐观。

对半潜船，虽然方形系数比较大，稳性比较好，但是由于作业状态下需要上升下潜，在相当长的时间范围内，船舶都只有艏艉楼两部分浮在水面上，水线面面积相对较小，而且这两部分的线型没有太大变化，所以常规的通过增加排水量以达到增加水线面面积的方法在此处失去效果［10］。所以从稳性考虑，非风雨密开口和非水密开口应遵循“少或无、靠中和舯、高可关”的原则布置［11］。这样可以改善诸如进水角、复原力臂、稳性正值范围等剩余稳性。

5 半潜船的实例

5.1 半潜船算例

下面给出国内某半潜船计算实例。表1所示。

表1 国内某半潜船主尺度参数

舱组的划分以自然横纵舱壁为界。利用现有压载水舱、机舱、防撞舱壁的横舱壁将船舶分成12个区域（zones）。与常规船舶不同之处在于，该半潜船中部有一段非连续水密甲板，舱组划分时将甲板突变处作为舱组前后壁。

对于航行状态取部分吃水（PLL）和夏季吃水（DSLL）两种状态；作业状态参考SOLAS对航行状态吃水定义，取最大下潜深度和其与最大下潜深度与空船吃水差60%之和的两种吃水状态（19 m，13.646 m）。GM值根据所选吃水载况给出。需要指出的是，同一吃水对应多种装载状况，相应有一系列的GM值，GM值的选取对破舱稳性计算结果有着直接影响［12］。

对于所有会导致累计进水的管路、通风、开口、最低进水点等都一一设置。不同于普通货船各舱室通风口的设置，由于半潜船货物甲板需要严格的水密完整性，所以本船各舱室（压载水舱、泵舱、机舱等）的通风口设置在上层建筑所在甲板。集中排列管路对破舱稳性提出新的要求，因为如果不在各舱安装单舱控制阀，就会对拥有共同空间的管路产生一损俱损的影响，这是设计者不愿意看到的。

各舱室的渗透率依据SOLAS规范选取。泵机舱等机械处所取0.85，各液体舱室取0.9。

规范规定该半潜船概率横准计算要求达到的分舱指数，R＝0.579 89。

表2～表6分别提供了半潜船概率破舱稳性计算清单及汇总。

表2 1个舱组破损下半潜船4种吃水的破舱稳性计算结果

表3 2个舱组破损下半潜船4种吃水的破舱稳性计算结果

表4 3个舱组破损下半潜船4种吃水的破舱稳性计算结果

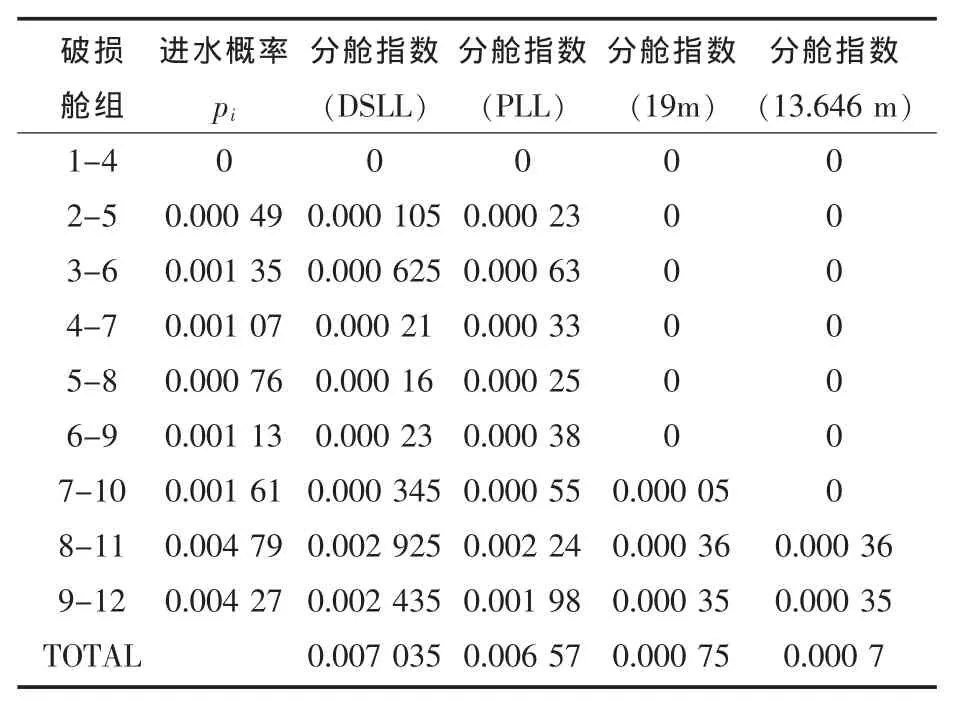
表5 4个舱组破损下半潜船4种吃水的破舱稳性计算结果

表6 各种舱组破损下半潜船4种吃水的破舱稳性计算结果汇总

由计算可知，对于航行状态：

A＝∑Ai＝0.432 38＋0.563 05＝0.995 43

即A＝0.995＞R＝0.580，满足破舱稳性要求；

对于作业状态：

A＝∑Ai＝0.453 64＋0.195 65＝0.649 28

即A＝0.649＞R＝0.580，满足破舱稳性要求。

5.2 半潜船破舱稳性讨论

本文给出某半潜船航行和作业状态下四种不同吃水情况的破舱稳性计算结果。结合上文对概率方法破舱稳性要素的分析，我们可以得到以下结论：

1）相对于航行状态，作业状态吃水较大，在此基础上，一旦发生破损，吃水增加直接导致进水角的减小，GZ曲线将提前截断，船舶破舱稳性下降；

2）对于设计好的半潜船，其横向舱壁都是确定的，破损区域划分相同，航行状态和作业状态的破损概率就相同；

3）因为破损后船舶的残存概率较小，连续多个舱组破损的情况对船舶总体破舱稳性达到的指数A的贡献较小，由于吃水较大，作业状态下这种情况更明显；

4）概率方法计算破舱稳性是建立在给定船舶吃水状态基础上的，而同一吃水可对应一系列的装载状态，这就给破舱稳性的计算提供了一定的空间，选取较佳的GM值进行破舱稳性计算；

5）与普通船舶相比，半潜船的舱室多为压载水舱。需要指出的是，在船舶航行状态，为保持船舶最佳浮态，个别压载水舱存在非满载情况。作业状态下，由于压载过程性决定了压载舱室自由液面的存在，所以在半潜船的破舱稳性计算中自由液面对稳性的修正很大程度上影响了船舶的破舱稳性，这是确定性方法中很明确的问题，由于本文主要讨论概率破舱稳性，采用浮力损失法，自由液面的影响不参与计算，本文不展开更深入的讨论。

6 破舱稳性的改进措施

船舶破损是船舶营运最担心遇到的问题，因为一旦发生海损事故，就会对人员、货物、环境造成巨大的经济损失。半潜船又多以运输昂贵的海洋结构物为主，业界对其破舱稳性尤为关注。

我们可以在船舶设计过程中注意下述事项：

1）设计适当的部分载重线时的KG值，最大载重线时的KG值应根据用途选择；

2）提高上层建筑物开口距水线面的位置，将进水角对GM的截断推后；

3）优化船舶边舱的设计，利用边舱的几何特性调节船舶平衡。

7 总结与展望

本文对半潜船航行和作业状态的破舱稳性进行了讨论，得到以下结论：

1）半潜船的破舱稳性与普通船舶类似，随着吃水的增加，破舱稳性下降；

2）半潜船作业状态的破舱稳性较差，因为出入水过程中只有艏艉楼两部分提供浮力，剩余干舷较小；

3）货物甲板在作业状态下对船舶残存概率的影响不计；4）鉴于上层建筑对深吃水下破损后的稳性影响较大，可以将更上层的甲板舱室做水密处理。

干货船、集装箱船等常规船舶的舱室的划分，如在全船的位置分布，舱室数目都已经有大量的参考文献，对船舶设计初期舱室的划分起到一定的指导作用，但是半潜船的破舱稳性几乎没有文献，随着半潜船市场的扩大，半潜船的概率破舱稳性优化分舱问题将成为热点。

我们还注意到，当今海事机构对半潜船的破舱稳性计算没有一个明确的衡准，所以加快对半潜船的破舱稳性衡准的研究将是各船级社的紧迫任务。

［1］冯志根.半潜船船型特点及其发展前景 ［J］.上海造船，2006（1）：49-51.

［2］KOELMAN H J，PINKSTER J.Rationalizing the practice of probabilistic damage stability calculations［J］.International Shipbuilding Progress，2003，50（3）：239-253.

［3］李晓，何炎平.压载舱的布置对FPSO破损稳性的影响［J］.中国造船，2005，46（5）：287-293.

［4］胡铁牛.货船概率破舱稳性研究－货船划分对分舱指数A的影响 ［C］／／第一届全国船舶与海洋工程学术会议，2000.

［5］严家文，吴永昌.货船破舱稳性概率算法软件（DAMCARGO）［J］.船舶，1996（1）：45-50.

［6］盛振邦，刘应中.船舶原理［M］.上海：上海交通出版社，2003.

［7］周晓明，张明霞，林焰，等.驳船的影响概率破舱稳性单因素研究［J］.中国造船，2007，48（4）：11-19.

［8］杨军.浅谈集装箱船的破舱稳性［J］.船舶设计通讯，2005（2）：49-51.

［9］林焰，纪卓尚.干货船分舱和破舱稳性概率衡准计算［C］／／第一届全国船舶与海洋工程学术会议第一届全国船舶与海洋工程学术会议论文集，2000.

［10］贾慧荣，何炎平，谭家华，等.南海2号半潜式平台深水改造方案破舱稳性研究 ［J］.中国海洋平台，2004，19（5）：28-31.

［11］贺俊松，胡铁牛，陈震，等.五体船破舱稳性计算与分析［J］.中国造船，2008，49（2）：29-36.

［12］曹才轶，严家文，蔡新功.基于遗传算法的船舶破舱稳性扶正措施优化研究［J］.中国造船，2008，49（2）：36-40.

Analysis on Damage Stability of Semi-submersible Vessel Using Probability Method

Hao Wei－wei1Zong Zhi1，2Lin Zhe1Chen Wei1
1 School of Naval Architecture，Dalian University of Technology，Dalian 116024，China 2 State Key Laboratory of Structural Analysis for Industrial Equipment，Dalian 116024，China

The ship subdivision and damage stability of semi－submersible vessels were studied by using worldwide general probability theory to the ship damage stability.After a number of computations，limit of compartment vertical separation，initial loading condition and geometry of side compartment were obtained and their relations and influences to the index A were established.The plots among related factors and general guidelines to ship design were generated.The computational results of stability requirement（SOLAS）were explained theoretically through an example of a semi－submersible vessel with probability calculation.Some design elements are listed which have value to evaluate index A in this paper.

new ship type；semi－submersible vessel；damage stability

U674.941

A

1673－3185（2009）04－12－06

2009-03-10

郝威巍（1984－），女，硕士研究生。研究方向：船舶与海洋工程设计制造。E-mail：xingzheid520＠gmail.com

宗 智（1964－），男，教授，博士生导师。研究方向：船舶与海洋工程。E-mail：zongzhi＠dlut.edu.cn