元认知理论在数学复习课中的运用

王 莉

美国儿童心理学家弗莱维尔指出：“元认知通常被广泛地定义为任何以认知过程与结果为对象的知识，或是任何调节认知过程的认知活动，它之所以被称为元认知，是因为其核心意义是对认知的认知。”可以说，元认知就是认知主体对自身心理状态、能力、任务目标、认知策略等方面的认识。同时，元认知又是认知主体对自身各种认知活动的计划、监控和调节。在复习课中运用元认知理论，能更有效地提高复习课的效率。

一、教师的“教”

1构建网络，掌握规律

在复习课教学中，教师必须揭示教材中各部分知识的内在联系，使学生从不同的角度加深理解，并通过比较以“求其异”、“求其同”，使学生掌握的知识系统化、深刻化，形成知识网络，同时从不同的方面去激活学生思维的灵活性、独创性和批判性，发展学生的元认知能力。为此，教师在教学中应采用“整体一部分一整体”的方法，重视学生正迁移能力的培养，防止负迁移的干扰。例如，中考中必考的现实背景的问题，一般是通过列方程或方程组、列不等式或不等式组、找函数关系二三种方法来解决。三种方法覆盖了初中三年的教学，教师当然要指导学生详细复习每一种方法，但更重要的是要提高学生在实战中的判断能力，使学生熟练地掌握规律，知道在什么情况下该用什么方法。这样可以帮助学生提高对任务目标、认知策略的认识。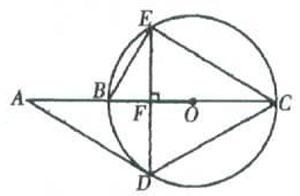

2展示思维，互相交流

讲解例题有两种方式。一是教师展示自己的思维过程，告诉学生解题时自己如何利用已知条件，遇到困难时如何做策略调整等，让学生借鉴。

例题：如图，已知AD是⊙O的切线，切点是D，直线AC经过圆心O，交⊙O于B、C两点，弦DE⊥AC。垂足为F，∠A=30°。(1)求LBED的度数。

(2)ADCE是否是等边三角形?请说明理由。

读完题目，教师可以这样说明自己的思路：“有切线的问题一般要连接圆心和切点，得∠ADO=90°。因为AA=30°，所以∠AOD=60°。要求LBED的度数，在这道有圆的题目中优先考虑圆周角，它等于所夹弧对的圆心角的一半，因此LBED=30°。第2问等边三角形的判定方法常用的有两个，我选择……”即使是错误的思路也可展示，重要的是展示教师是如何将思路调整到正确的解题方向上的。

二是教师通过如“你是怎么想的?”“你为什么这样想?”这些问题来引导学生展示自己的思维过程，让学生互相交流、启发，学会对问题解决的进程进行积极的、自觉的监控。

3组织反思，总结经验

一节复习课不仅要让学生重温已学过的知识，还要使学生知道各知识点之间的联系，一般的问题思考方法，老师、同学的方法是否能借鉴，自己的方法好在哪里，它能不能用于解决其它问题等。

如在上例讲解完例题后，教师向学生提问：“解题时我们首先应该关注什么?”学生回答：“题目提到的已知量和未知量。”教师继续提问：“本题涉及的量是什么?”学生回答：“与圆相关的线和角。”教师追问：“这些线与角是怎样联系在一起的?”学生会给出一系列定理，说出它们的关系。教师点出，这就是一般的解题思路。接下来请学生分析第2问两种证法的优劣，与其他同学共同品评。由于学生问存在差异，因此在做课堂小结时，教师的点拨应循序渐进，兼顾先后，让不同的学生在数学上有不同的发展。

学生的思维能力就在这样的不断探索和回顾反思中得到提高，学生的元认知能力因而也得到培养和开发。

二、学生的“学”

除在课堂上接受老师的引导之外，学生自己本身也应该有意识地掌握一些元认知方法。这里介绍美国数学家波利亚的自我提问法。这个方法以各个认识阶段的一系列问题帮助学生进行自我观察、自我监控、自我评价，不断促进学生自我反省。

理解问题阶段的问题：未知条件是什么?已知条件是什么?用已知条件足以求出未知量吗?

拟定计划阶段的问题：过去见过这类题吗?若见过，它是否以稍微不同的方式出现?我能用与未知条件相同或相似的熟悉问题的解法来解决这道题吗?如果不能，我能从已知条件中找到(推导出)什么有用的东西?我是否用上了所有的条件和数据?

执行计划阶段的问题：能清楚地认定每一步都是对的吗?能证明它是对的吗?

回顾阶段的问题：我能检验结果的正确性吗?我能检验推理过程吗?我能在其他问题上运用这个结果或方法吗?

这个方法不妨印发给学生人手一份，让学生做作业时先看看，配合课堂教学，加深印象。如上例的课后作业可布置两道与例题相似(有与圆相关的线和角)的作业，再布置一道有特殊四边形还有圆的题目。学生若遇上困难，可对照以上方法看哪些环节自己没考虑周全，以加强自我意识，提高知识迁移能力。这样做，学生综合运用知识的能力会提高，心理素质也会提高，从而保障了学生在考试中的稳定发挥。

(责编王学军)