基于冲量变轨原理的地球同步卫星有限推力变轨策略

彭 坤，徐世杰

（北京航空航天大学宇航学院，北京100191）

基于冲量变轨原理的地球同步卫星有限推力变轨策略

彭 坤，徐世杰

（北京航空航天大学宇航学院，北京100191）

推力有限时，地球同步轨道卫星在远地点变轨的弧段很长，会导致较多的燃料消耗。基于冲量变轨原理，研究了地球同步轨道卫星远地点有限推力多次变轨问题，提出了具有星下点约束的最省燃料变轨方案，给出了每次变轨的推力方向和点火起止时刻及最优中间过渡轨道。仿真结果验证了该方案的有效性。

冲量变轨；地球同步卫星；有限推力；远地点变轨

1 引 言

从近地椭圆停泊轨道进入地球同步轨道是一种常见的变轨方式，工程上一般采用在远地点多次变轨的策略。以往地球同步轨道卫星都利用固体发动机来进行变轨。其特点是推力大，作用时间短，可认为是冲量式变轨。现在，卫星多采用液体发动机进行变轨，这种发动机可进行多次点火，前一次点火中产生的误差可在以后多次点火期间修正，而且在变轨期间其低推力特性使卫星容易维持其三轴稳定性。这时，冲量假设不再成立，而最省燃料的有限推力变轨问题归结为求解大型的非线性两点边值问题，但求解过程非常复杂。

文献[1]应用递推二次规划算法进行有限推力远地点变轨参数寻优，但算法比较复杂。文献[2]研究了推力较小时在远地点采用多次变轨的最优变轨过程，但存在初始猜测问题，且入轨时没有精度限制。文献[3]利用动态规划技术研究了多冲量推力作用下的最优交会问题，但采用了冲量式变轨且仅适用于共面椭圆轨道。文献[4]利用极大值原理给出了交会问题中最优推力弧段的几个性质。文献[5-6]研究了三轴稳定模式下的有限推力轨道转移问题，及交会时卫星在三维空间的最省燃料有限推力轨道转移问题。文献[7]讨论了求解有限推力轨迹优化问题的直接打靶方法。文献[8]运用遗传算法对有限推力轨道拦截问题进行了优化。上述讨论中，文献[5-8]均只研究了一次变轨的过程，没有涉及多次变轨问题，这将使变轨误差无法得到修正。

由文献[6]可知，卫星在最省燃料异面有限推力轨道转移过程中推力方向在惯性空间几乎成固定值。为了简化计算，可假设变轨过程中发动机的推力方向在惯性系中不变，且始终在节点惯性系的xoy平面内。在此基础上，可利用冲量变轨的原理估算每次变轨中轨道要素的变化所需的燃料消耗和点火信息，通过优化中间过渡轨道的轨道要素来减少燃料消耗。此方法避开了求解两点边值问题，简化了计算过程，而由于推力弧问题产生的误差可通过以后几次变轨进行补偿。

本文利用上述方法研究了卫星从近地椭圆轨道到地球同步轨道最省燃料的多次变轨策略。基于推力大小不变、推力方向在节点惯性系的xoy平面内不变的假设，讨论了每次变轨时有限推力点火信息的求取方法（包括点火时刻、熄火时刻和推力方向）。仿真算例中考虑了卫星在进入地球同步轨道时的星下点约束，仿真结果验证了该方法的有效性。

2 轨道动力学模型

在整个变轨过程中，卫星始终绕地球飞行，因此卫星的动力学方程可用第一组轨道摄动方程[9]表示

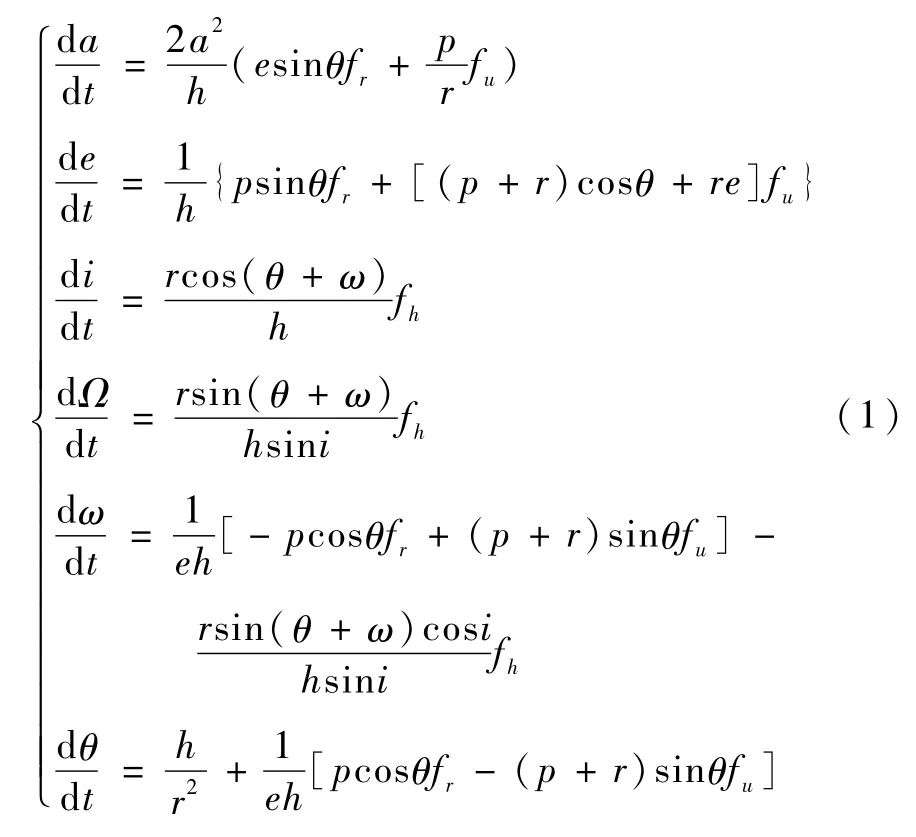
式中，a、e、i、Ω、ω和θ分别为轨道半长轴、偏心率、轨道倾角、升交点赤经、近地点辐角和真近点角。p是半通径，p=a（1-e2），h是轨道角动量μ为地心引力常数，r是卫星到地球中心的距离，r=p/（1+e cosθ），fr、fu和fh分别为地球扁率、日月引力及发动机推力的合加速度在径向、切向和角动量方向的分量。

由文献[6]的结论，可设推力方向只在节点惯性系的xoy平面内变化，故可用偏航角ψ来表示推力加速度的径向分量fT_r、切向分量fT_u和角动量方向分量fT_h，其关系式为

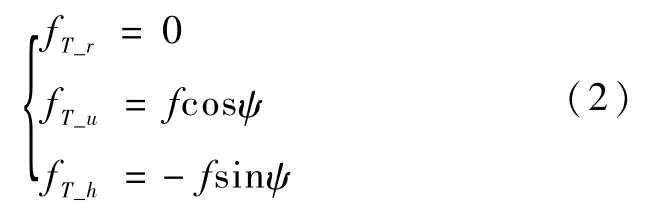
其中，节点系和轨道系的关系如图1所示。

3 基于冲量变轨的变轨点火信息求取方法

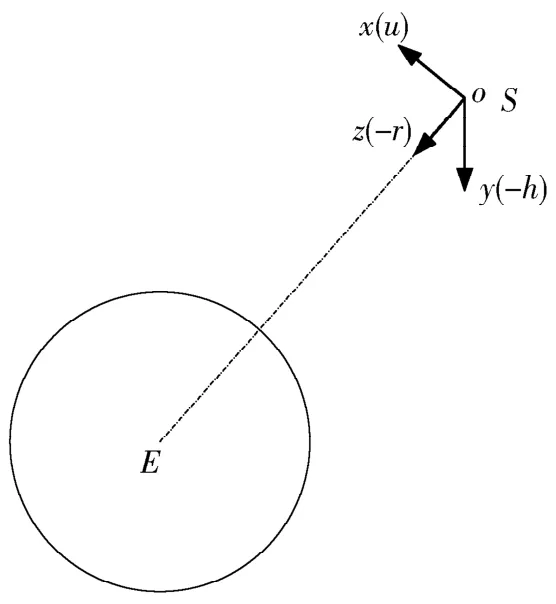
图1 节点系和轨道系的关系图

一般单冲量变轨方式有以下三种：一是仅改变轨道倾角，不改变半长轴时（在升或降交点施加冲量），需要的速度增量是Δvi=2v0sin（Δi/2）；二是仅增大轨道半长轴，不改变倾角时（在远地点施加冲量），需要的速度增量是Δva=vf-v0；三是既变倾角又变半长轴时，需要的速度增量是Δv=其中，v0为施加冲量前速度，vf为施加冲量后的最终速度，Δi为轨道倾角变化量。

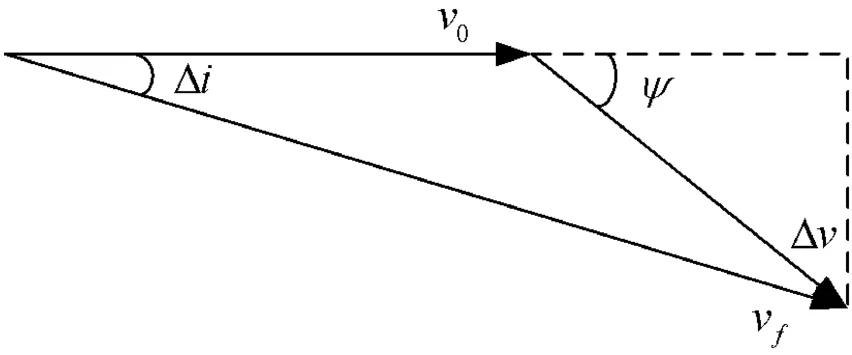
图2 变轨的速度增量

根据文献[6]，可设最省燃料的推力方向在惯性系上是不变的。在变轨时间不长（即推力弧不长）的情况下，可用冲量变轨原理来算出改变卫星轨道要素所需的速度增量Δv，把Δv的方向作为变轨过程的推力方向。由此可求得发动机的偏航角为ψ=arcsin（vfsin（Δi）/Δv），如图2所示。同时，可由Δv的大小算出变轨过程的燃料消耗Δm和点火时间Δt，其计算公式如下

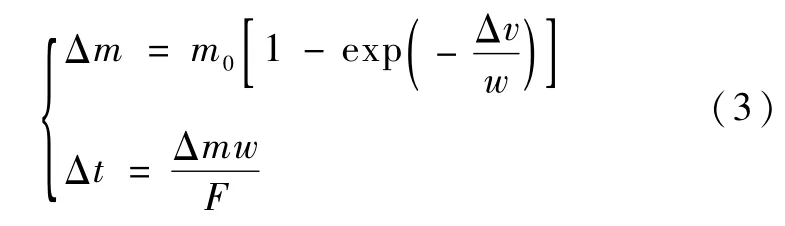
式中，m0为卫星的初始质量，w为发动机的排气速度，它是发动机比冲与重力加速度的乘积，即w=Ispg，F为发动机的推力。

有了推力方向和点火时间，只需求出点火时刻就能知道完整的变轨点火信息。为了减小变轨过程中推力弧产生的误差，可将远地点时刻设为变轨过程的中间时刻，即点火时刻和熄火时刻对称地设在远地点时刻两侧。

4 最省燃料的多次变轨方案设计

在变轨过程中，如果采用一次变轨方案，需要很长的点火时间，会产生一段很长的推力弧段，造成大量燃料损失。如果采用多次变轨，推力弧段会比较短，有利于节省燃料，但推力发动机的工作次数有一定限制，多次变轨开关机会缩短其寿命，而且多次变轨过程比较复杂，不利于优化。一般可采取3～4次变轨完成任务，前两次变轨将椭圆轨道的轨道要素调整至地球同步轨道的轨道要素，最后1～2次变轨用于微调以消除前两次变轨产生的误差。

由于最后1～2次变轨的主要目的是微调轨道要素，故而关键是优化前两次变轨的轨道要素。而第一次变轨的初始轨道要素为已经给定的近地椭圆轨道的轨道要素，第二次变轨的最终轨道要素为地球同步轨道的轨道要素，因此只需优化第一次变轨后的最终轨道要素。其中，前两次变轨总的燃料消耗Δm与第一次变轨后的半长轴a和轨道倾角i的关系如下式所示

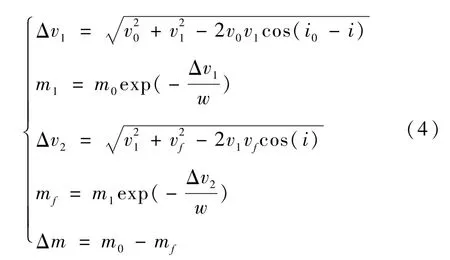
式中，v0，v1，vf的表达式分别为

下面考虑一项具体的变轨任务。设近地椭圆轨道的轨道参数为：a=24546km，e=0.7319，i=28.49°，Ω=323°，ω=180°。卫星在格林威治时间2009年12月30日16时整的平近点角为M=1.06°，以此时刻为变轨过程的初始时刻。地球同步轨道的轨道参数为：a=42164km，星下点经纬度为（100°，0°）。卫星的初始质量为m=3200kg，发动机的推力为F=490N，比冲为Isp=309s。以下采用基于冲量变轨的变轨点火信息求取方法来设计变轨方案。

燃料消耗Δm随第一次变轨后的半长轴a和轨道倾角i变化的曲面关系如图3所示。由图可知，对应于燃料消耗Δm最小的第一次变轨后的参数为：a=2.454632×107m，i=28.49°和a=4.25×107m，i=0°。但这两组数据都相当于一次变轨完成。而一次变轨在用有限推力推进的情况下会浪费燃料，故不采取。

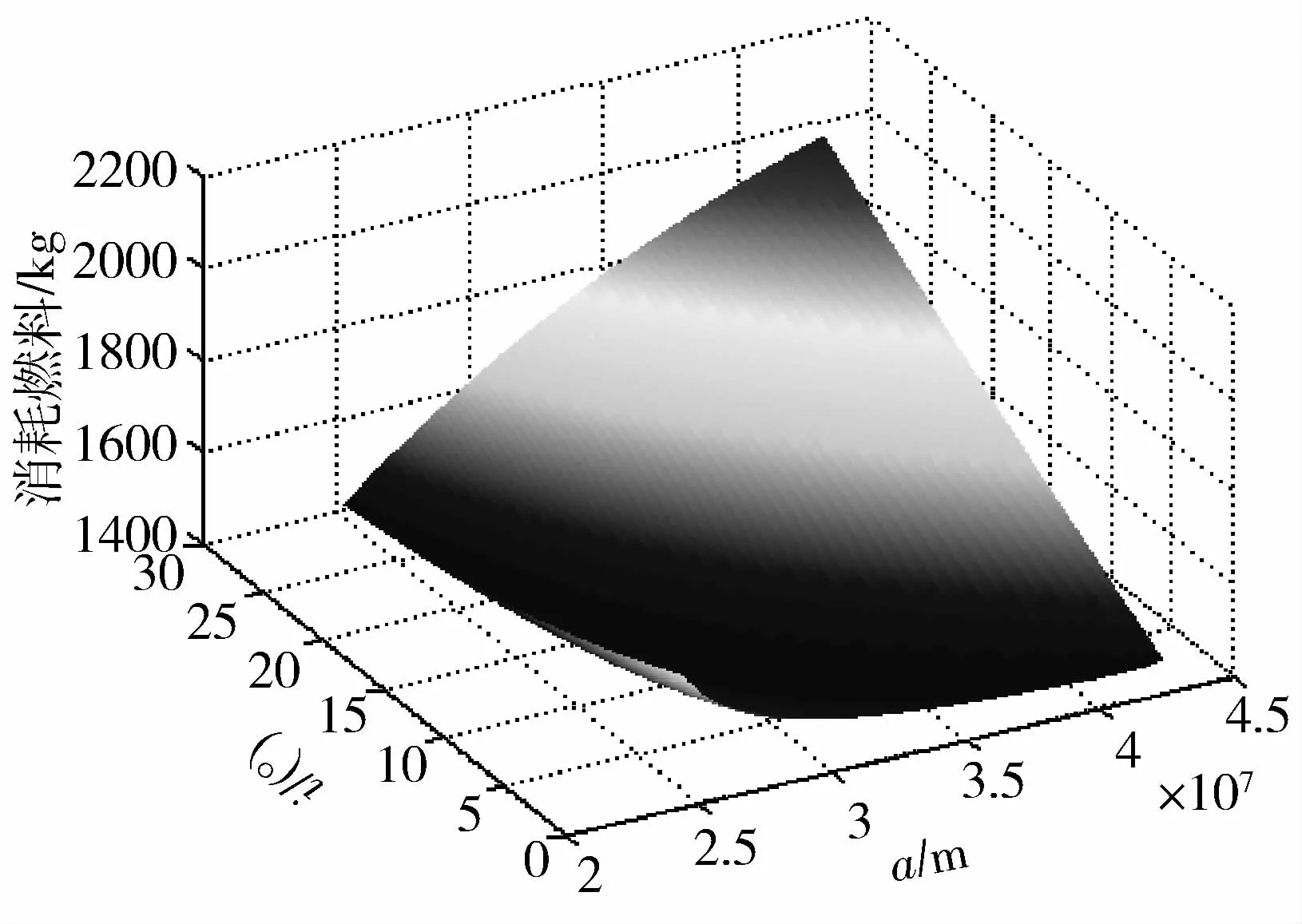
图3 Δm随a和i变化的曲面图

在这种情况下，可每隔2°取一个倾角值，计算每个倾角值下最小的Δm值及相应的a值，并求出前两次变轨的点火时间Δt1和Δt2。为了避免变轨时间过长，应使两次变轨的时间大致相同。通过计算可知，当a=2.805×107m，i=12°时，燃料消耗最小且两次变轨时间大致相同。

5 各变轨段的点火信息设计

（1）第一次变轨点火信息

取第一次变轨后的半长轴和轨道倾角为a=2.805×107m，i=12°，则可由第2节中的变轨点火信息求取方法计算出第一次变轨的变轨参数：M=159.3846°，ψ=52.8656°，Δt1=4383.4s。仿真可得当t=16740s时，平近点角M=159.3817°，因而其变轨参数如表1所示。仿真可得变轨后实际的轨道半长轴和轨道倾角为a=2.7912×107m，i=12.0757°。

（2）第二次变轨点火信息

为减小变轨误差，取第一次变轨后的实际轨道要素a=2.7912×107m，i=12.0757°计算第二次变轨的变轨参数，可算得M=161.8888°，ψ=36.0639°，Δt2=4669.5s。取t=63303.732s（M=161.8599°），仿真可得a=4.2542×107m，i=0.2038°。但平近点角产生突变（如图4所示），故对点火时刻进行调整。经过反复调整可得，取M=168°为点火时刻时，平近点角变化曲线比较平缓（如图5所示）。当M=168°时，t=64092s，故取它为第二次变轨点火时刻。

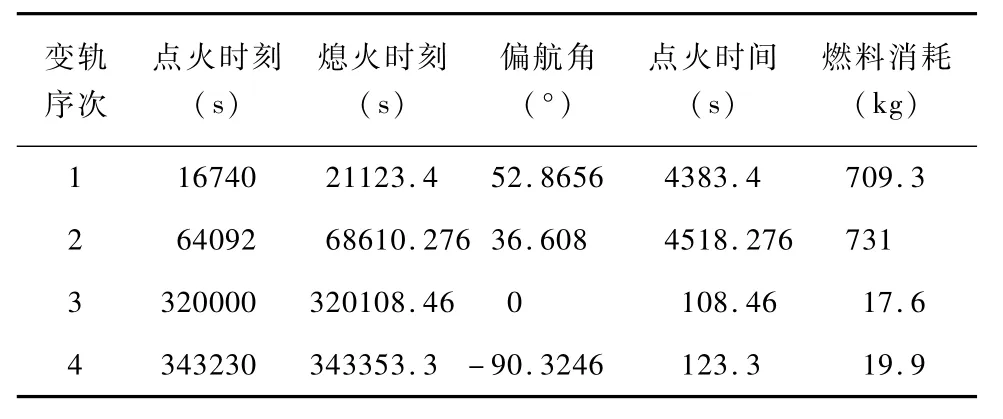
表1 四次变轨的变轨参数

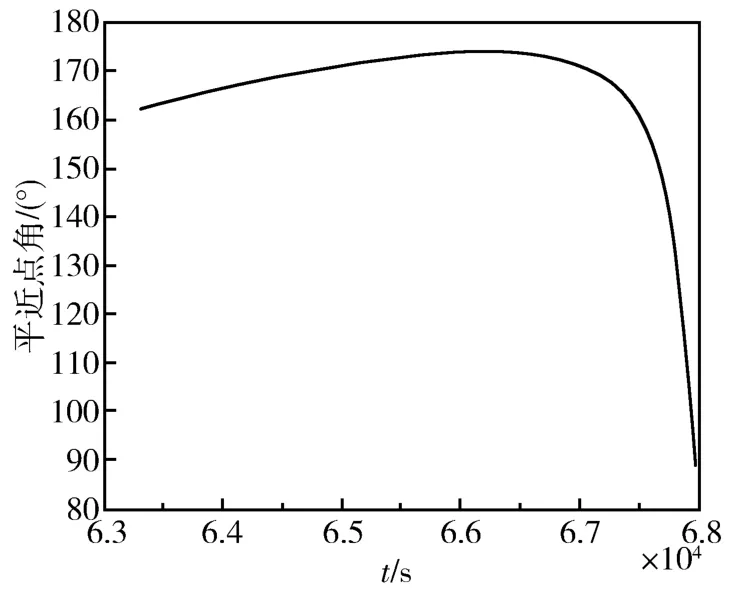
图4 M=161.8599°时的平近点角变化曲线

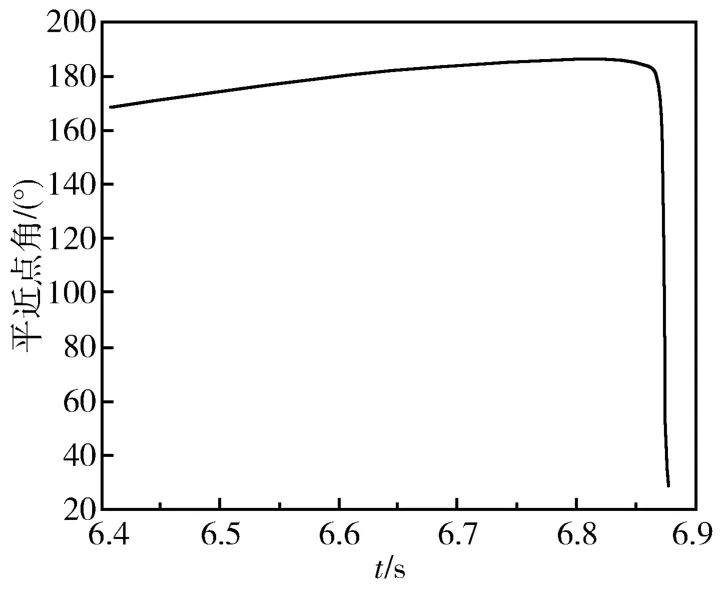
图5 M=168°时的平近点角变化曲线

在确定第二次变轨熄火时刻时，应兼顾星下点位置要求，使卫星在经过第三次漂移后正好在远地点时的星下点位置为（100°，0°）。表2列出了卫星分别漂移1、2、3圈到达指定经度时对应的第二次变轨熄火时刻的半长轴acoast和漂移时间tcoast。

表2 漂移圈数不同时的轨道半长轴和漂移时间

如取熄火时刻tf=68657s（M=180°），可算得a=4.1766×107m，与表2中第三组数据相近。仿真得t=68610.276s时，a=4.1462×107m。用第三组数据进行第三次漂移仿真得M=182.9639°。当t=320000s时，M=180.0046°，星下点经度为95.9836°。若能调整a=4.13553×107m，则漂移后星下点经度为100.0002°。此时固定点火时间，调整偏航角使ψ=36.608°时，a=4.13553×107m。综上所述，第二次变轨的变轨参数如表1所示。

（3）第三次变轨点火信息

第三次变轨的主要目的是调整a，i的值，其中轨道倾角调整比较难，且有增大的趋势，故主要调整半长轴。当半长轴增大到目标值时，停止变轨。仿真可得其变轨参数如表1所示。

（4）第四次变轨点火信息

当卫星完成三次变轨时，轨道倾角i还存在0.6492°的误差，因此必须再次变轨以修正轨道倾角误差。而要改变轨道倾角，不改变半长轴，应在升或降交点施加冲量。同样运用第2节的方法可求出此次变轨的变轨参数，如表1所示。

6 仿真结果

在数值计算中，采用四阶龙格—库塔积分算法，变轨段步长为0.3s，漂移段步长为10s。卫星在四次变轨中总计的燃料消耗为1477.8kg，由于产生推力弧，比理论的燃料消耗最优值（1452.5kg）多1.74%。四次变轨后卫星到达指定星下点位置的地球同步轨道，其中前两次变轨主要是大范围改变半长轴a、偏心率e和轨道倾角i，后两次变轨分别修正了半长轴a和轨道倾角i的误差。图6描绘了卫星的整个飞行轨迹，从图中可看出前三次变轨基本在远地点位置附近，第四次修正轨道倾角的变轨在卫星轨道的降交点位置附近。

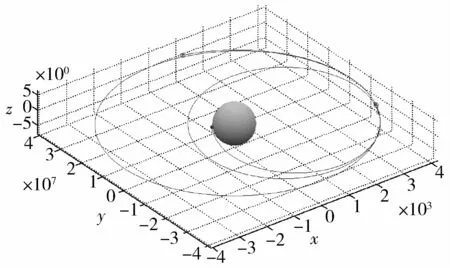
图6 卫星飞行轨迹

7 结 论

通过引入最省燃料异面有限推力轨道转移过程中推力方向在惯性空间不变这一假设，利用冲量变轨原理处理了有限推力轨道转移问题。这种方法可以避开求解大型的两点边值问题，使计算过程大大简化。本文给出了利用冲量变轨原理求解最省燃料的每次变轨点火信息和最优中间过渡轨道的方法。在第二次变轨时选择合适的轨道半长轴和适当的漂移时间，使卫星的星下点在第三次远地点变轨时到达指定的经度位置。算例表明，本方法能够得到较精确的变轨结果，包括每次变轨的最优推力方向和点火起止时刻及最优中间过渡轨道。由于推力弧的存在，实际仿真的燃料消耗比理论最优值要稍多一些。

[1] 赵旭，李果，李铁寿.基于递推二次规划算法的燃料最优有限推力远地点变轨[J].航天控制，1997，15（2）：23-28

[2] 王小军，吴德隆，余梦伦.地球同步卫星远地点最省燃料小推力多次变轨[J].中国空间科学技术，1995，15（4）：1-9

[3] 谌颖，黄文虎.多冲量最优交会的动态规划方法[J].宇航学报，1993，14（4）：1-7

[4] 谌颖，陈祖贵，刘良栋.常推力作用下飞行器固定时间最优交会[J].中国空间科学与技术，1998，18（4）：1-7

[5] 荆武兴，吴瑶华，王学孝，杨涤.小卫星三轴稳定模式下的有限推力轨道转移[J].中国空间科学技术，1996，16（5）：51-57

[6] 荆武兴，吴瑶华.基于交会概念的最省燃料异面有限推力轨道转移研究[J].哈尔滨工业大学学报，1998，30（2）：124-128

[7] 王华，唐国金，雷勇军.有限推力轨迹优化问题的直接打靶法研究[J].中国空间科学技术，2003，23（5）：51-56

[8] 汤一华，陈士橹，徐敏，万自明.基于遗传算法的有限推力轨道拦截优化研究[J].西北工业大学学报，2005，23（5）：671-675

[9] 肖业伦.航天器飞行动力学原理[M].北京：宇航出版社，1995

Finite Thrust Maneuver Strategy for the Geostationary Satellite Based on Impulse Orbit Transfer

PENG Kun，XU Shijie
（School of Astronautics，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

In the case of finite thrust apogee maneuver for the geostationary satellite，the fuel consumption increases due to the long burn arc.Based on the impulse orbit transfer principle，the finite thrust multi-impulse apogee maneuver for the geostationary satellite is studied in this paper.The minimum fuelmulti-impulse apogeemaneuver strategy with the constraint of sub satellite point is obtained.The thrust direction and firing time of each maneuver and the optimal intermediate transition orbits are given.Simulation results validate the effectiveness of the proposed method.

impulse orbit transfer；geostationary satellite；finite thrust；apogee maneuver

V448

A

1674-1579（2008）06-0048-04

2008-08-15

彭 坤（1984-），男，湖北人，博士研究生，研究方向为小推力轨道转移的控制、建模与仿真研究（e-mail：bhkpeng@126.com）。