高姿态稳定度敏捷卫星的VSCMGs操纵律研究

2008-12-20邢林峰孙承启

空间控制技术与应用 2008年6期

关键词：姿态控制标称稳定度

邢林峰，孙承启，汤亮

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

高姿态稳定度敏捷卫星的VSCMGs操纵律研究

邢林峰1，2，孙承启1，2，汤亮1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

研究采用变速控制力矩陀螺群（VSCMGs）作为姿态控制执行机构的高姿态稳定度敏捷卫星的操纵律设计问题。将VSCMG分为控制力矩陀螺（CMG）和动量轮（MW）两种工作模式，针对每种工作模式进行奇异性分析，并给出逃避奇异的方法。为了获得较好的控制效果，还研究了VSCMGs转子转速向标称转速平衡的方法以及通过调整转子轴构型使转子转速快速返回到标称值的方法。最后通过对算例进行仿真，验证了所设计的操纵律的有效性。

变速控制力矩陀螺；奇异；操纵律

1 引言

从航天应用需求分析可知，未来的高分辨率传输型成像卫星需要具有快速姿态机动能力，此类卫星也称为敏捷卫星。采用控制力矩陀螺（CMG，controlmoment gyro）作为姿态控制的执行机构可满足敏捷要求，但由于CMG的力矩输出精度较低，较难满足姿态稳定度优于0.001（°）/s的要求。转子转速可变的单框架控制力矩陀螺通常也称为变速控制力矩陀螺（VSCMG，variable speed control moment gyro），采用VSCMG可以较好地解决卫星快速、大角度机动与稳态附近的高姿态稳定度之间的矛盾。在快速机动时，主要由框架角变化提供很大的控制力矩，但快速机动时转子转速也在变化，并对控制力矩提供补充，此时为CMG工作模式；在稳态附近通过转子转速变化提供高精度控制力矩，框架角不再发生变化，此时为动量轮（MW）工作模式。文献[1]描述了美国预研中的激光中继卫星，对采用VSCMG作为执行机构的姿态控制展开了一系列的研究。文献[2]提出用框架轴不平行的两个VSCMG构成变速控制力矩陀螺群，就能解决SGCMGs的构型奇异问题，并给出系统的动力学模型。文献[3]给出系统的动力学模型，并设计了一种基于Lyapunov方法的姿态控制律。文献[4]描述了在VSCMGs的操纵律中引入加权广义逆。

本文以敏捷卫星高姿态稳定度控制问题为背景，将VSCMG分为CMG和MW两种工作模式，CMG模式可满足敏捷要求，MW模式可满足高姿态稳定度要求；设计了相应的操纵律解决了奇异问题；最后以采用金字塔构型VSCMGs的卫星为例，并在考虑了执行机构的力矩输出能力和精度的前提下进行了数值仿真，验证了所设计的操纵律的有效性。

2 系统动力学模型简介

在星体坐标系中，内部装有N个VSCMG的刚体卫星的角动量为[2-3]

式中，Te为作用于系统的外力矩，ω的上标“×”表示ω的叉乘反对称方阵。

3 Lyapunov方法姿态控制律介绍

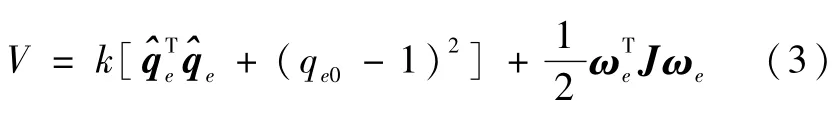
式中k为正的参数，J同式（1）中的定义。

将式（2）代入式（4），并忽略作用于航天器的外力矩Te后可得

式中，

显然，若

式中K为对称正定的系数矩阵。则有

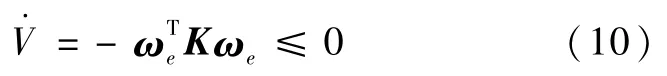
由式（10）可知，当且仅当ωe=03×1时，=0。为负半定，系统是李亚普诺夫稳定的。由式（4）可知，当ωe=03×1，=0时=03×1。根据拉萨尔不变集定理可知，系统对于误差姿态和误差角速度ωe是渐近稳定的。令

则稳定条件（9）可写为

式中Tr即是期望的姿态控制力矩，这一控制力矩由VSCMGs提供。

4 VSCMGs的操纵律

式（11）中矩阵C的列向量的模远大于矩阵B的列向量的模，且一般框架角加速度很小，在此前提下，忽略式（11）中的项。这样，VSCMGs的力矩输出方程可写成如下形式

4.1 VSCMGs的奇异性分析

本文从快速姿态机动和高姿态稳定度的需求考虑，定义了引言中描述的CMG和MW两种工作模式，每种模式都需要有逃避奇异的能力。

VSCMG在CMG模式下的奇异与SGCMG的奇异相似，奇异度采用下式描述

VSCMG在MW模式下，框架轴不动，即.γ=0，通过调节转子转速输出高精度控制力矩。此时式（13）变为E˙Ω=Tr，结合式（8）可知，通过调节转子转速输出的力矩使之分别平行于As中的各列向量。rank（As）＜3称为VSCMG的MW模式陷入构型奇异，此时转子轴共面或平行，仅靠调节转子转速已不能保持三轴姿态控制能力，所以在进入MW模式前，须调整转子轴构型，以避免MW模式奇异。定义MW模式奇异度为

4.2 CMG模式与MW模式之间的切换条件

航天器在稳态附近可以描述为：误差角速度的模‖ωe‖2和误差四元数矢量部分的模都小于某一预定的阀值，即

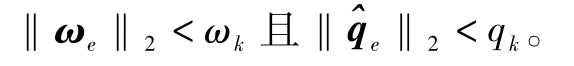
式中，ξk为MW模式下有较好三维控制能力时的ξ阀值。

4.3 输出力矩的操纵律

式（13）的加权最小范数解为[1，4]

式中加权矩阵为

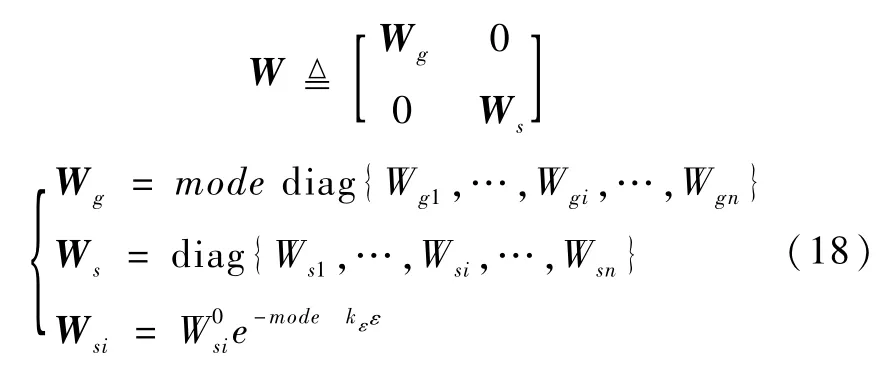
加权矩阵W既可以实现在CMG和MW方式之间的切换；又可以在CMG模式下的控制律中起到在框架转动和转子转速变化输出力矩之间的分配和调节的作用。

4.4 VSCM Gs的零运动

与SGCMG相似，VSCMG在CMG模式下的零运动总是存在的。根据广义逆定理逃离CMG模式奇异的零运动为

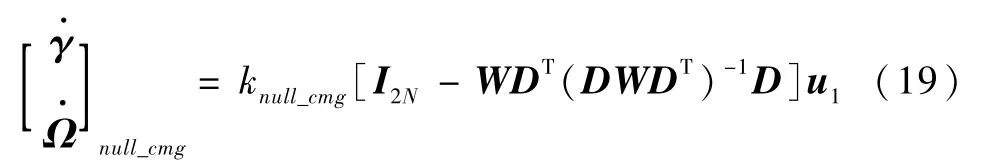
式中，knull_cmg为待定系数，且knull_cmg＞0，u1为2n维矢量的列向量。空转运动的要点在于选择待定系数knull_cmg和矢量u1，要使奇异度ε的增值为正，需有效地避开CMG模式陷入奇异。

待定标量knull_cmg取值越大，框架脱离CMG模式奇异的速度就越快。但是框架转动角速度是有上限的，因而knull_cmg选取如下：

式中，αnull_cmg为一正常数，εnull为是否需要空转的阀值。

令避免MW模式奇异的零运动指令为

knull_mw为待定系数，且knull_mw＞0，u2为2n维矢量的列向量，转子轴构型空转指令为

在进入MW工作模式前，需要提前调整好转子构型，所以越接近稳态，这种需求就越迫切。而当大角度机动时，为CMG工作模式，逃离CMG模式奇异比逃离MW模式奇异更重要。knull_mw选取如下：

式中αnull_mw为一正常数。

4.5 转子转速向标称转速平衡的功能

系统应有转子转速向标称转速平衡的功能，即应使各转子的转速尽量相互接近，且尽量向标称转速接近。这样可以使系统具有CMG模式下均匀的三轴姿态控制能力和MW模式下的较大的角动量容量。令为标称转速。定义一个表征转子转速相对标称转速误差分布的指标函数

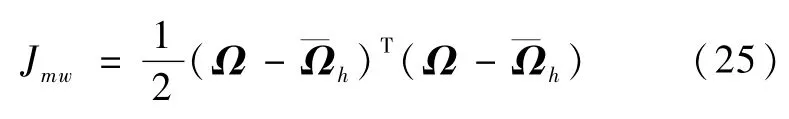
式中，Jmw为非负，其值越小，表明转子转速平均值越接近标称转速，且各转子转速彼此相近。在转子操纵律中加入平衡空转项Su3，u3为n维待定矢量的列向量。

式中，S是N()E上的投影矩阵，因此Su3位于E的零空间上，Su3不会产生对星体的姿态控制力矩，所以称之为转子空转。

当u3=-KrST时取得最大负值，使Jmw尽量变小。则此时转子转速向标称转速接近，其空转指令为

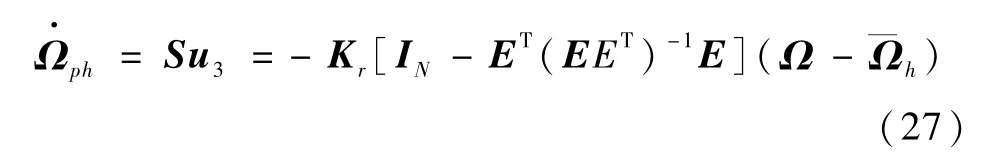
式中Kr为一正常系数。

4.6 转子转速卸载

在MW工作模式下，为了防止某些转子转速过快以致饱和或者过慢以致在切换到CMG工作模式时该VSCMG失去大力矩输出能力，因此必须限定转子转速（只能在一定的范围内调节）。当超出预定范围时，需对转子转速进行卸载。对转子转速Ω进行快速卸载的基本原理就是在总角动量不变的前提下，通过调整转子轴构型和转子转速，重新分配各个转子的角动量。

令sign_xz为描述是否需要卸载转子转速的变量，sign_xz=1表示需要卸载，sign_xz=0表示不需要卸载。工作模式的切换可用下式描述

当转子转速需要卸载时，即sign_xz=1时，首先由MW工作模式切换到CMG工作模式，即设置mode=1，接下来对Ω进行快速卸载。转子转速向标称转速调整的输出力矩为

式中km为正系数。

为使VSCMGs整体输出控制力矩为零，框架轴转动输出力矩应等于-Tm。

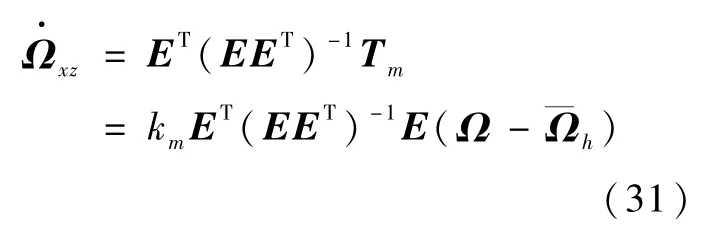
待定标量km与转子转速卸载快慢有关。需在进入MW工作模式前，提前调整好转子转速。但ε较小时逃离CMG模式奇异比转子转速调整更重要。km选取如下

式中βm为正常值系数。

综上所述，VSCMGs的操纵律如下：

5 数值仿真

本节对操纵律进行数值仿真。假设有一颗小卫星运行在高度为645km的圆轨道上，采用金字塔构型的4个VSCMG作为姿控用的执行机构，卫星质量特性（单位kg·m2）为：IB=diag｛350，300，450｝，Ics=diag｛0.1，0.1，0.1，0.1｝，Ict=Icg=diag｛0.03，0.03，0.03，0.03｝。其它参数为：

卫星每180s绕滚动轴机动一次，目标姿态角度以30°、0°、-30°、0°、30°和0°…的顺序周期性地重复。

图1为在操纵律中引入避免CMG模式奇异和MW模式奇异的两个零运动后的奇异度。整个机动过程中，CMG模式和MW模式都没有陷入奇异。

图2和3为在操纵律中没有引入避免CMG模式奇异和MW模式奇异的两个零运动时的奇异度。整个机动过程中的很大一部分时间都陷入CMG模式奇异或MW模式奇异。

从图1～3说明逃离CMG模式奇异和逃离MW模式奇异的零运动操纵律的重要性。

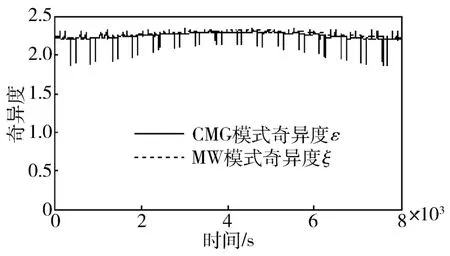
图1 多次快速机动过程中的奇异度

图4为滚动机动30°过程中，为增加MW模式的角动量容量，从CMG模式进入MW模式之前，要通过转子空转指令，使转子转速接近标称转速的情况。

图2 不引入零运动操纵律时MW的模式奇异度

图3 不引入零运动操纵律时CMG的模式奇异度

图4 VSCMG的转子转速趋向标称转速的情况

6 结束语

本文讨论了VSCMGs的奇异性，研究了操纵律，并设计了操纵律中的各种加权系数。通过对一颗卫星的仿真，验证了所设计的避免奇异、转子转速向标称转速平衡等操纵律的有效性。

[1] Marcello R，Agrawal B N.Attitude dynamic/control of dual-body spacecraft with variable-speed controlmoment gyros[J].Journal of Guidance，Control and Dynamics，2004，27（4）：513-525

[2] Schaub H.Feedback control law for variable speed controlmoment gyros[J].The Journal of Astronautical Sciences，1998，46（3）：307-328

[3] 贾英宏.航天器姿态与能量一体化研究[D].哈尔滨工业大学博士论文，2004

[4] 汤亮.使用控制力矩陀螺的航天器姿态动力学与控制问题研究[D].北京航空航天大学博士论文，2005

[5] 章仁为.卫星轨道姿态动力学与控制[M].北京航空航天大学出版社，1998

VSCMGs-Based Steering Law Design for a High Attitude Stability Agile Satellite

XING Linfeng1，2，SUN Chengqi1，2，TANG Liang1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

The fast-maneuver and high-attitude-stability control problem of agile satellites is addressed by employing the variable speed control moment gyros（VSCMGs）as the actuator.A steering law is proposed by using the Lyapunov approach.The VSCMG can work in two modes，control moment gyro（CMG）mode or moment wheel（MW）mode.The singularity problem of each working mode is analyzed.An approach is proposed to avoid the singularity.To improve the control performance，the problem of matching the VSCMGs wheel's speed with its nominal value is also studied.A method for rapid dumping of wheel's speed is presented by adjusting the formation of wheels.Numerical simulations illustrate the feasibility and performance of the proposed steering law.

variable speed controlmoment gyro；singularity；steering law