鲁棒滤波技术在脉冲星导航中的应用*

2008-12-20魏春岭刘良栋

空间控制技术与应用 2008年6期

关键词：鲁棒脉冲星X射线

熊凯，魏春岭，刘良栋

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

鲁棒滤波技术在脉冲星导航中的应用*

熊凯1，2，魏春岭1，2，刘良栋1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

提出将鲁棒扩展卡尔曼滤波（REKF）用于增强X射线脉冲星导航系统克服星表误差影响的能力。指出星表误差可以看作模型不确定性的一部分，采用鲁棒滤波技术进行处理。对REKF和传统扩展卡尔曼滤波（EKF）的性能进行对比。仿真结果表明，存在星表误差的情况下，采用REKF算法进行航天器导航，能够获得优于EKF的定位精度。

航天器；自主导航；脉冲星；扩展卡尔曼滤波；鲁棒滤波

1 引言

X射线脉冲星导航作为一项新兴的航天器自主导航技术，是当前国内外航天技术领域的研究热点之一[1-2]。美国国防高级研究项目局（DARPA）从2005年开始资助基于X射线源的自主导航定位（XNAV）计划，研究所需的原始数据由Chandra号X射线观测站提供，并计划2009年在国际空间站上进行X射线探测器性能测试。DARPA还支持美国海军研究实验室（NRL）进行了X射线脉冲信号源选择和X射线探测器原理样机的研制工作。另外，在NASA的SBIR基金支持下，Microcosm公司研究了基于脉冲星的导航和授时技术。国内，如中国科学院、中国空间技术研究院、北京航空航天大学和国防科技大学等单位也在积极开展相关技术的研究工作。

典型的脉冲星导航方式是基于航天器轨道动力学模型建立状态方程，基于脉冲星角位置信息和脉冲星时间模型建立观测方程，采用适当的滤波算法处理由X射线探测器获得的脉冲到达时间（TOA）观测量，估计得到航天器的位置和速度矢量。受测量手段的限制，用于建立观测方程的脉冲星角位置数据不可避免地会存在误差。脉冲星角位置误差被称为星表误差，星表误差是影响脉冲星导航系统性能的主要因素之一。采用脉冲星观测量差分技术是消除星表误差影响的方法之一[3]，但采用该项技术要求同时获得两个或多个航天器的TOA观测量，不适合用于仅对单个航天器进行导航的情况。

事实上，星表误差可看作模型不确定性，存在模型不确定性的情况下，基于最优滤波理论设计的KF及其改进算法，实际上都是次优的。为了解决这一问题，人们进行了多年的研究工作；其中，有关鲁棒滤波的研究取得了较大进展。与最优滤波算法不同，鲁棒滤波的设计指标不是使估计误差方差最小，而是使模型中的不确定因素对估计精度的影响最低。近些年来，针对模型中存在的线性化误差、范数有界的不确定性、随机不确定性和测量延迟等多种类型的不确定性，提出了多种鲁棒滤波算法[4-5]，但鲁棒滤波的研究多是针对假想的系统进行的，在解决实际问题方面所做的研究相对较少。

本文首先介绍利用脉冲星TOA观测量实现航天器导航的方法，以及星表误差对导航精度的影响；接着，给出适用于非线性不确定系统的REKF算法；最后，通过数学仿真验证REKF的定位精度优于传统EKF算法。

2 基于脉冲星的航天器导航方法

X射线脉冲星是宇宙空间中以稳定的周期高速自转的中子星，这类天体能够沿磁极方向发射X射线束，由于其自转轴与磁极方向不一致，脉冲星的转动带着辐射波束在宇宙中扫过一个巨大的锥形，当波束扫过观测者时，观测者就获得一个X射线脉冲信号。某个脉冲信号到达航天器与到达太阳系质心（SSB）的时间之差反映了航天器相对于SSB的位置矢量robs在脉冲星视线矢量n（p）上的投影，如图1所示。

通过航天器上的X射线探测器记录得到脉冲信号到达航天器的时间，通常称为脉冲到达时间（TOA）观测量，符号中的上标p用于区分不同的脉冲星。根据建立在SSB的脉冲星时间模型精确地预测得到脉冲信号到达SSB的时间，c表示光速。

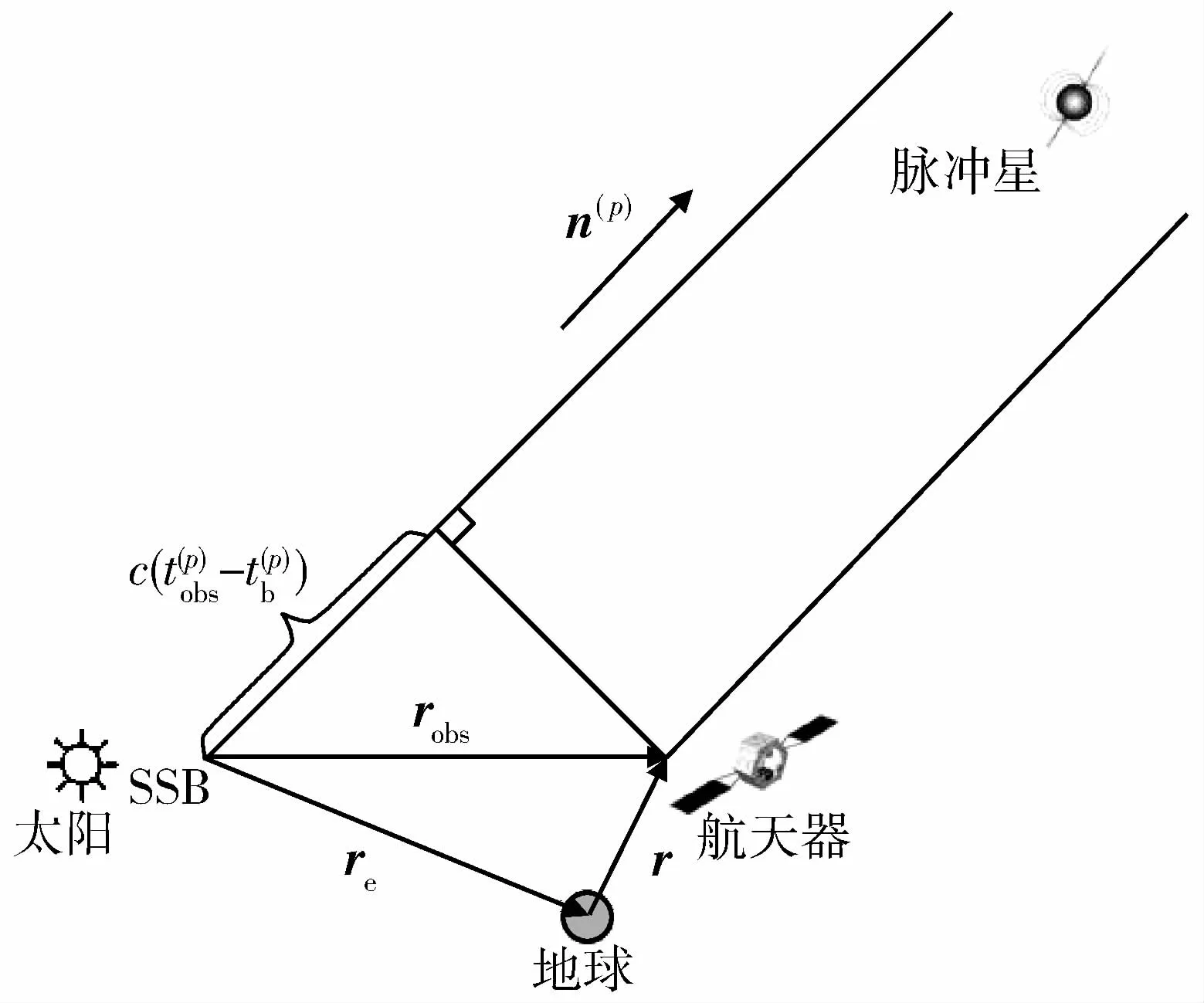
图1 基于脉冲星观测量的航天器定位原理

下面介绍利用EKF处理TOA观测量，通过递推计算得到航天器位置矢量估计值的方法。要进行滤波器的设计，首先要选择状态变量，并建立描述状态量和观测量关系的系统模型。选择航天器位置矢量r和速度矢量在地心惯性坐标系的3个分量为状态向量，即

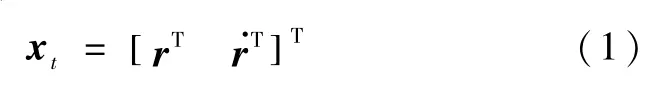
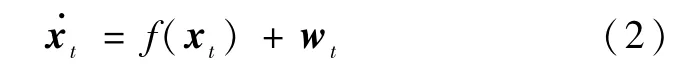
式中，

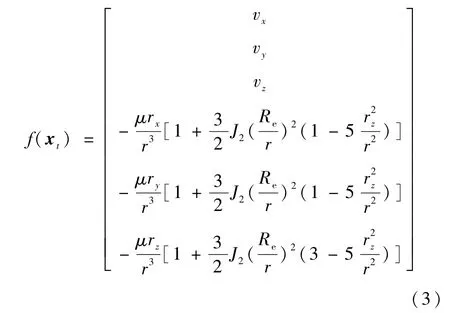
其中，μ为地球引力常数，J2为二阶带谐项系数，Re为地球平均赤道半径表示地心距；wt表示系统噪声，用来描述各摄动项的建模误差。

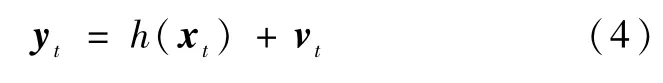
式中，

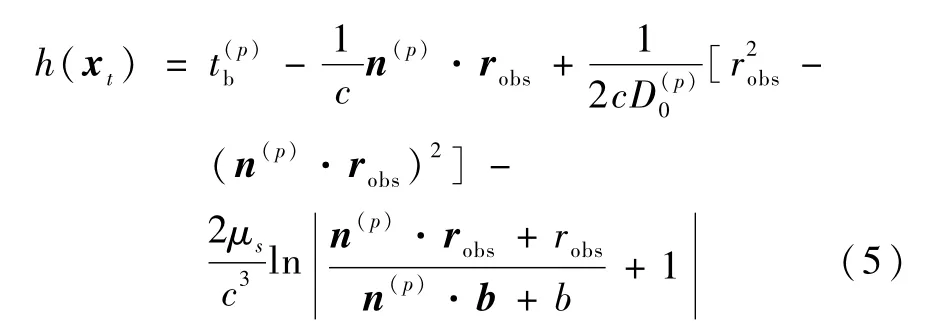
其中，D（p）0表示SSB到脉冲星的距离，b是SSB相对于太阳质心的位置矢量，μs是太阳引力常数，式（5）是在精确的时间转换方程的基础上忽略高次项得到的，并且未考虑航天器时钟偏差、整周模糊度和色散效应误差的影响；vt表示与系统噪声wt无关的测量噪声。

视线矢量n（p）根据脉冲星的赤经α（p）和赤纬δ（p）计算得到，计算公式为

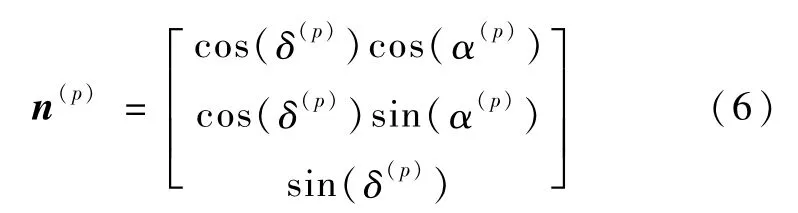
但通过天文观测获得的α（p）和δ（p）均带有误差，用表示带有误差的赤经和赤纬。其中，Δα（p）和Δδ（p）表示星表误差，利用ˆα（p）和ˆδ（p）计算得到的带有星表误差影响的视线矢量记为ˆn（p）。星表误差对航天器定位精度的影响如图2所示。

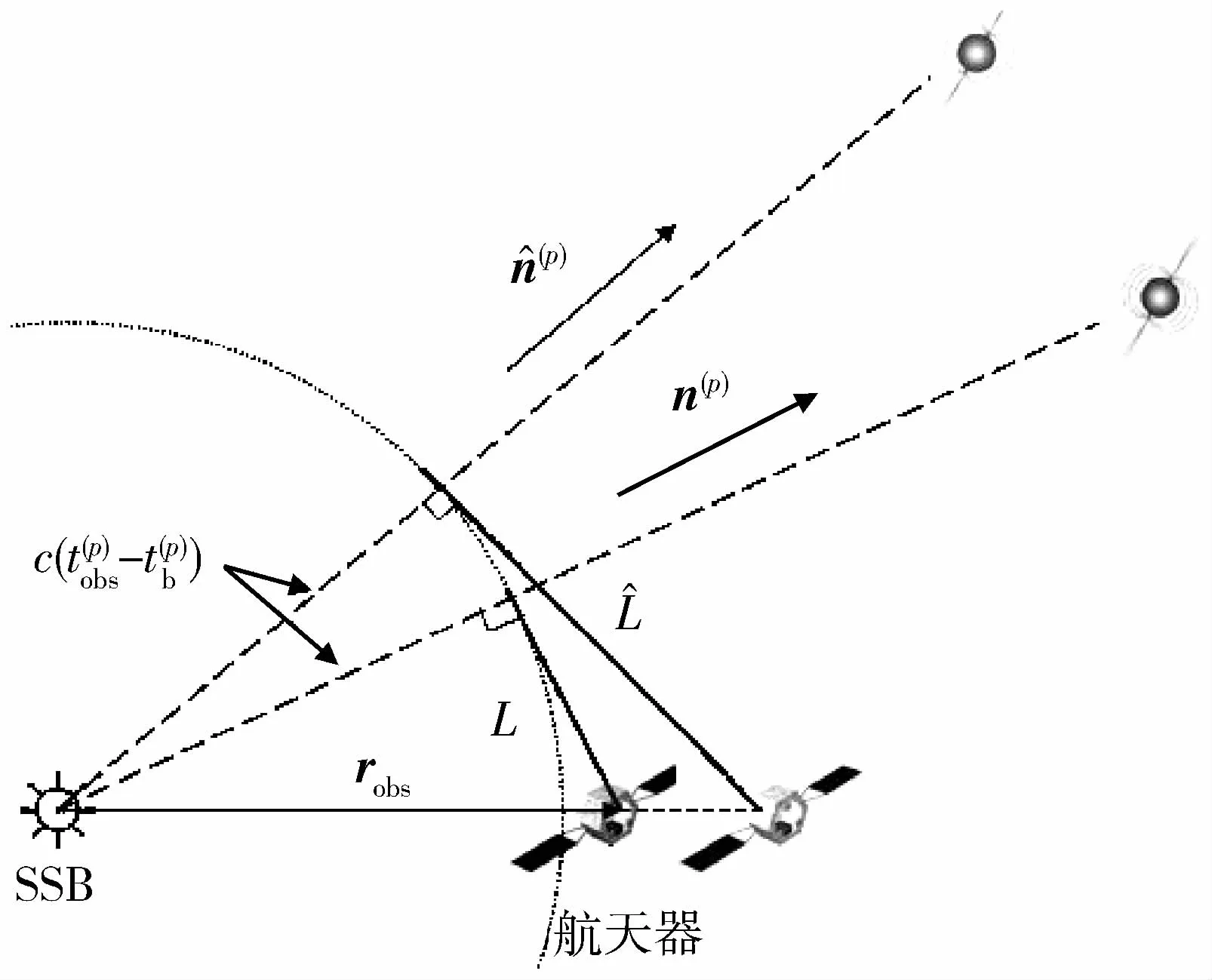
图2 星表误差对脉冲星导航系统的不利影响

不难看出，如果模型中的脉冲星视线矢量是不准确的，那么，即使TOA观测量是准确的，根据该观测量得到的航天器位置也是不准确的。以现在的技术测量脉冲星角位置，精度介于0.01″～0.001″之间，对应数百米的定位误差，并且星表误差对定位精度的影响随航天器与SSB距离的增大而增大。

3 鲁棒扩展卡尔曼滤波算法

本文将鲁棒滤波技术用于克服星表误差的影响，基本思路是通过不确定模型描述带有模型不确定性的系统，并根据所建立的模型形式和给定的指标要求推导相应的滤波方程。考虑如下所示的离散非线性不确定系统

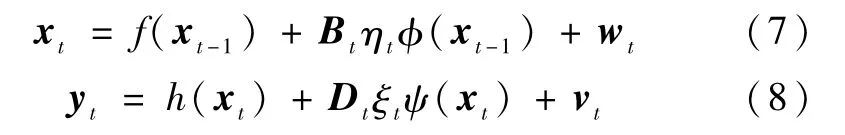
式中，xt和yt分别表示状态量和观测量，wt和vt分别是系统噪声和与系统无关的测量噪声，Bt和Dt是已知的时变矩阵，φ（·）和ψ（·）为已知的与状态变量有关的函数，未知参数ηt和ξt满足条件

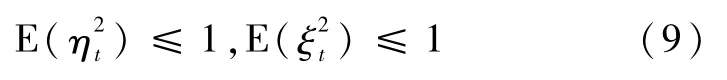
式中，Btηtφ（xt-1）和Dtξtψ（xt）用于描述模型不确定性。

沿用KF理论的思想，REKF算法还是采用KF中的“预测-更新”结构形式，即

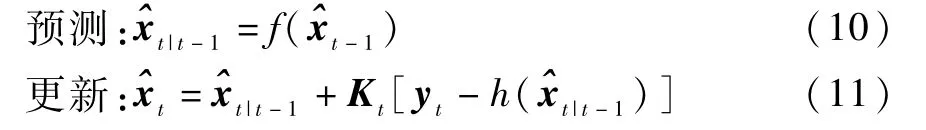
但滤波增益阵Kt的设计方法与KF的不同。REKF的设计要求为：对于如式（7）和（8）所示的非线性不确定系统，设计Kt，使得估计误差的方差Σt=不大于与Kt有关的正定矩阵序列Pt（t=0，1，2，…），并使Pt的值最小。其中，第一个要求的意义是保证滤波稳定性；第二个要求的意义在于提高算法的估计精度。

REKF的设计方法为：首先，根据系统模型（7）、（8）和滤波器结构形式（10）、（11）构造估计误差的表达式，并推导相应的估计误差方差阵的表达式；接着，应用有关矩阵不等式的研究成果，得到Σt的上界Pt；然后，通过设计滤波增益阵Kt，使得估计误差上界Pt最小；最后，结合具体系统中对模型不确定性的分析结果优化滤波参数。所设计的滤波增益阵可通过如下定理进行表述。

定理1.对于由式（7）和（8）描述的非线性不确定系统，假定条件（9）成立，如果存在正常数γ和矩阵L，使得下列离散Riccati差分方程

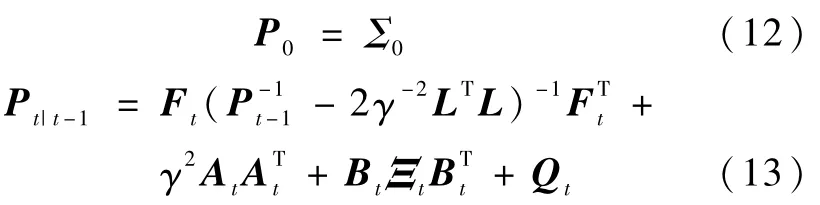
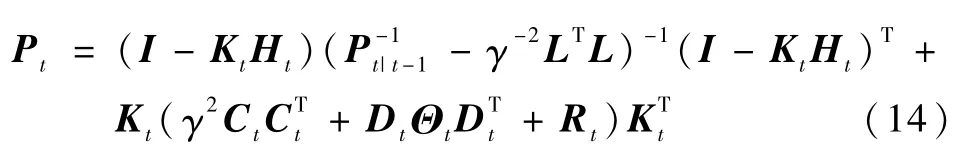
有正定解Pt，并且

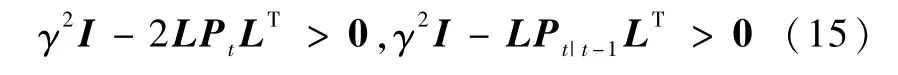
那么，对于0≤t≤n，如式（10）和（11）所示的增益阵为

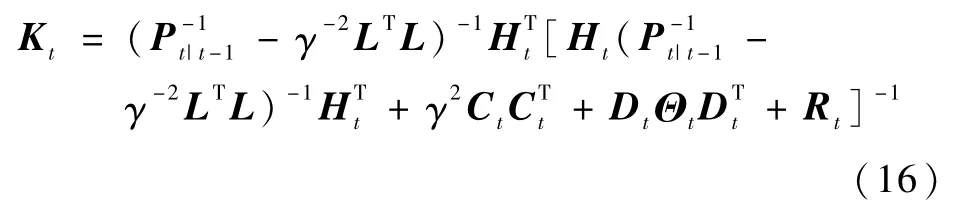
定理1中的矩阵Ft和Ht分别表示状态方程和观测方程的雅克比矩阵，At和Ct用于刻画线性化误差的大小，ψT（xt）]。具体的公式推导可参见文献[7]。

与EKF算法不同，REKF的设计指标不是使估计误差最小，而是使估计误差的上界最小；采用这一指标的原因在于：存在模型不确定性的情况下，估计误差方差阵Σt的表达式中存在未知参数，不能直接用于滤波增益的设计。注意到在REKF的设计过程中考虑了模型不确定性的影响，主要体现在不确定模型中的Btηtφ（xt-1）和Dtξtψ（xt）两个误差项。应用REKF的关键是合理的选取Bt和Dt的值，使得所建立的不确定模型能够有效地描述实际系统中不确定性的影响，具体的说，所选择的Bt和Dt应使式（9）所示条件得到满足。

4 仿真结果

以轨道半长轴为12275km，偏心率为0.0038，轨道倾角为109.8°的LAGEOS-1卫星为例，验证本文提出的REKF算法的有效性。在仿真生成卫星轨道数据的过程中，考虑了地球非球形引力、太阳引力、月球引力、太阳光压和大气阻力的影响。假设各航天器上X射线探测器的有效面积为1m2，取背景辐射光子流量FluxB=0.005photons/（cm2·s），分时段观测3颗脉冲星B0531+21、B1821-24和B1937+21，航天器上的指向装置每1000s进行一次换向，TOA测量噪声根据文献[1]所述方法确定。设3颗脉冲星对应的赤经和赤纬误差以及相应的误差界如表1所示。

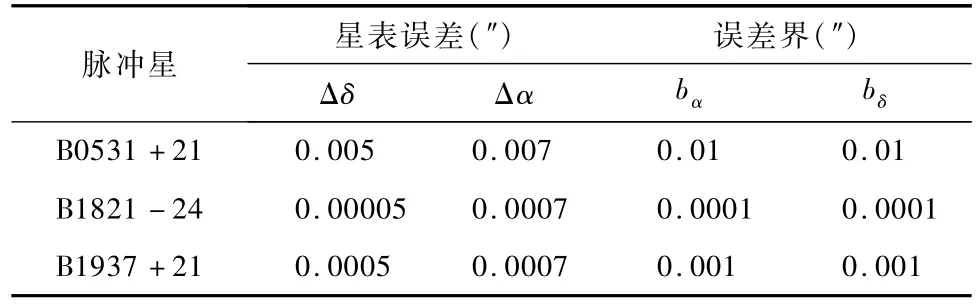
表1 脉冲星星表误差及其误差界

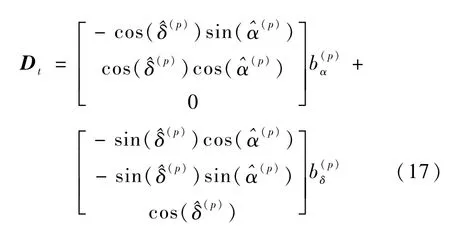
相对于星表误差而言，线性化误差和轨道动力学模型的建模误差对估计精度影响较小，因此，仿真中忽略线性化误差和轨道动力学模型J2项以外的建模误差，即选择At、Bt和Ct为0矩阵。根据式（16）的要求，选择γ=εmax（eig（LP0LT））0.5，L=I。设初始位置误差为5km，初始速度误差为10m/s，选择系统噪声方差阵其中q1=2×10-5m，q2=2×10-4m/s，初始估计误差方差阵，其中p1=10km，p2=25m/s。TOA观测量每100s进行一次更新，仿真时间为LAGEOS-1卫星的3个轨道周期。

分别采用EKF和REKF算法进行10组仿真，计算得到的三轴位置矢量的估计误差均方根，如图3所示。两种滤波算法在最后一个轨道周期内的位置估计误差均方根如表2所示。在X射线脉冲星导航系统中，模型不确定性主要体现为星表误差，赤经和赤纬的误差会对EKF性能产生不利影响。而REKF将有关脉冲星赤经和赤纬的误差界的先验知识用于滤波器的设计，所得的增益阵Kt能够减小受星表误差影响较大的TOA观测量的修正作用，并充分发挥受星表误差影响较小的TOA观测量的作用。因此，对于受到星表误差影响的脉冲星导航系统而言，REKF的性能优于传统EKF算法。

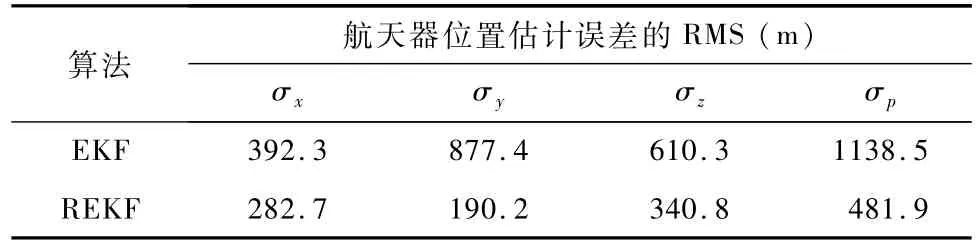
表2 REKF与EKF算法精度对比

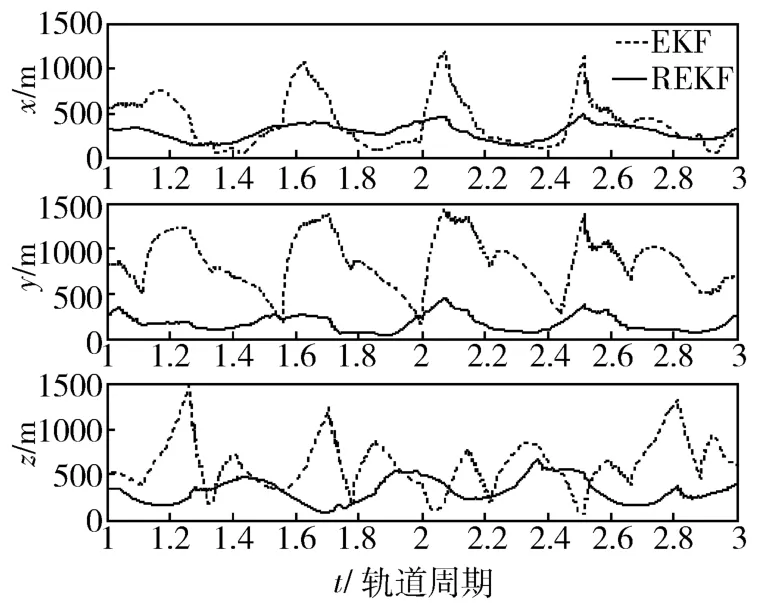
图3 EKF和REKF的估计误差均方根曲线

5 结论

本文研究了通过鲁棒滤波技术来改善X射线脉冲星导航系统性能的方法。所提出的REKF算法将脉冲星赤经和赤纬的误差界用于建立不确定模型，并将不确定模型用于优化滤波增益阵的设计，从而获得了更加合理的滤波增益阵。因此，采用REKF算法能够有效地削弱星表误差的不利影响，改善脉冲星导航系统的性能。

[1] Sheikh S I，Pines D J，et al.Spacecraft navigation using X-ray pulsars[J].Journal of Guidance，Control，and Dynamics，2006，29（1）：49-63

[2] Wood fork DW.The use of X-ray pulsars for aiding GPS satellite orbit determination[D].MS thesis，Department of the Air Force，Air University，2005

[3] Xiong K，Wei C L，Liu L D.The use of X-ray pulsars for aiding navigation of satellites in constellations[J].Acta Astronautica，to be published

[4] Seo J，Yu M J，Park C G，Lee JG.An extended robust H∞filter for nonlinear constrained uncertain systems[J].IEEE Transactions on Signal Processing，2006，54（11）：4471-4475

[5] Calafiore G.Reliable localization using set-valued nonlinear filters[J].IEEE Transactions on System，Man，and Cybernetics-Part A：Systems and Humans，2005，35（2）：189-197

[6] 章仁为.卫星轨道姿态动力学与控制[M].北京：北京航空航天大学出版社，1998

[7] 熊凯.基于脉冲星的空间飞行器自主导航技术研究[R].中国空间技术研究院博士后研究报告，2008

Application of Robust Filtering in Pu lsars-Based Navigation

XIONG Kai1，2，WEIChunling1，2，LIU Liangdong1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

The robust extended Kalman filter（REKF）is adopted to overcome the unfavorable effect of the pulsar's position error on the pulsar's navigation system in this paper.It is shown that the pulsar's position error can be seen a smodel uncertainty，and the effect of the uncertainty can be reduced by using the robust filtering technique.The performance of the REKF is illustrated in comparison with the standard EKF.Numerical simulation shows that the REKF is more accurate than the EKF for spacecraft navigation in the presence of pulsar's position error.

spacecraft；autonomous navigation；pulsar；extended Kalman filter；robust filter