柔性航天器姿态快速机动的自适应控制方法*

张国琪，丁建钊

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

柔性航天器姿态快速机动的自适应控制方法*

张国琪1，2，丁建钊1

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

研究带柔性附件航天器的姿态快速机动控制问题。根据带柔性附件的航天器的动力学模型推导并建立其特征模型。基于所建立的特征模型设计一种自适应控制方法，该方法设计简单，控制器参数物理意义明确，便于调试，可同时实现航天器的姿态快速机动控制和弹性附件的振动快速抑制。理论分析和数学仿真表明，该方法对控制器参数及被控对象的不确定性有很强的鲁棒稳定性和鲁棒性能，能取得比工程中常用的比例-微分（PD）控制更快的机动速度和更好的控制性能。

姿态快速机动；柔性航天器；自适应控制；特征模型

1 引 言

随着空间技术的发展，空间飞行器的结构及动力学建模变得越来越复杂。航天器配备大型柔性结构（如大型太阳能电池帆板、大型柔性天线和大型空间桁架结构等）成为现代复杂航天器在结构设计方面的一大显著特点。柔性结构的出现给航天器的动力学建模和控制都带来了很大的困难。在动力学建模方面，因柔性结构本质上属于分布参数系统，所以需结合连续介质力学用偏微分方程模型对其建模，不过由于存在材料特性和几何结构上的非均匀一致性、复杂的边界条件以及尚未研究清楚的弹性动力学难题等多种因素，使得柔性结构的动力学建模问题至今仍是力学领域重点研究的前沿课题。在控制方面，柔性结构的出现给航天器的控制系统设计带来很大的困难，国际上已经多次发生因控制器设计不当导致柔性航天器控制系统失稳或者未能达到设计指标的重大问题。

由于柔性结构控制问题在航空航天及机械制造领域的重要性和潜在价值，自上个世纪60年代起，关于柔性结构的动力学与控制问题就得到了国内外相关领域学者的广泛关注，并进行了重点研究，取得了重要的研究成果［1-6］：文献［7］综述了关于柔性机械臂的动力学研究现状及有待研究的前沿问题；文献［8］综述了关于柔性机械臂的控制方法的研究现状。总体来讲，目前关于柔性结构的动力学研究主要集中于小变形慢速运动，且多局限在平面运动，而迄今关于做大变形快速运动和空间运动的柔性结构动力学的研究结果很少，还需进一步研究。

由于柔性结构的动力学模型存在很大的不确定性，因此有实用性的控制方法必须具有一定的鲁棒性。文献［9］采用 μ综合技术，对柔性结构设计了鲁棒控制器，通过实验研究表明该方法的控制效果在很大程度上仍然依赖于对柔性结构真实动力学模型的了解。自适应控制经过半个世纪的发展取得了大量研究成果［10-11］。本文针对柔性结构航天器的大角度快速机动控制问题，提出一种基于特征模型的自适应控制方法。该方法设计简单、鲁棒性强，通过适当地选取控制器设计参数，可比常用的PD控制取得更好的控制性能。

2 动力学模型及特征建模

2.1 动力学模型

如图1所示，一类中心刚体带柔性附件的航天器单轴姿态运动的动力学模型为［12］

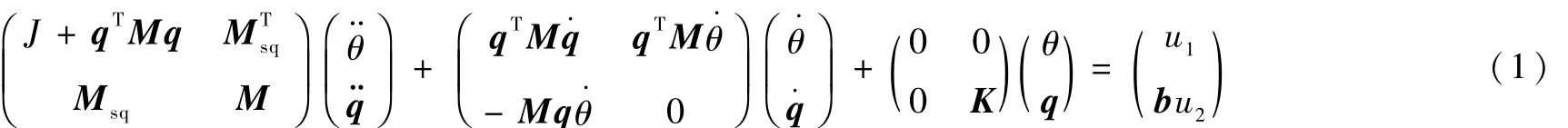
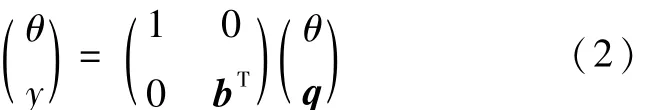
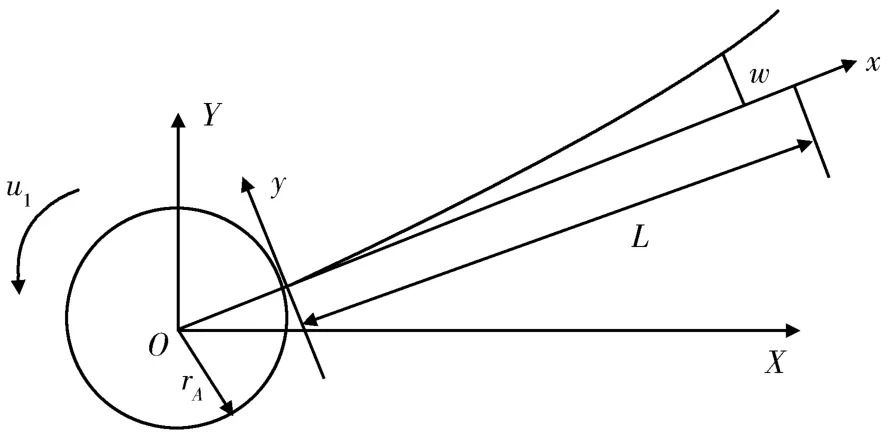
图1 中心刚体带柔性附件的航天器示意图［12］

式（1）和式（2）中各矩阵具体元素的表达式为

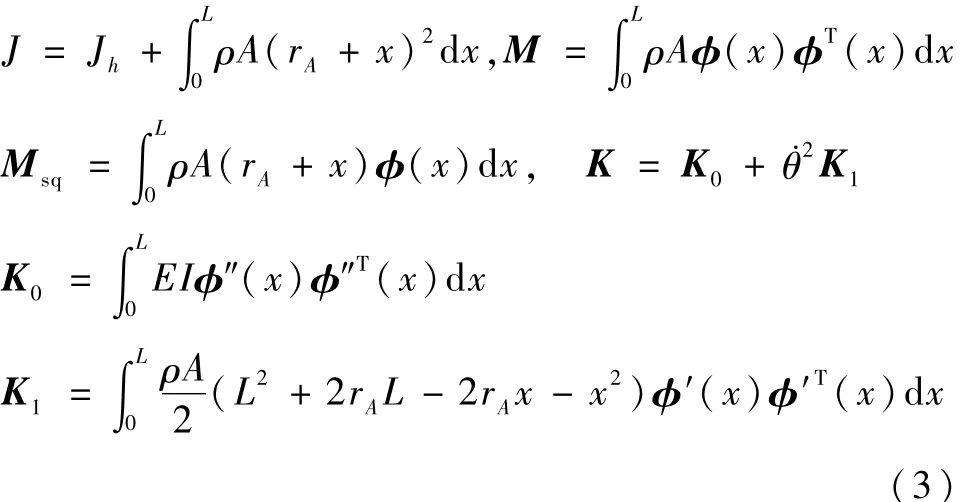
其中，ρA是柔性附件的线密度，rA是中心刚体半径，Jh是中心刚体转动惯量，EI是弯曲刚度，L是柔性附件长度，θ是本体姿态角，y是弹性附件变形测量输出，u1是姿态控制力矩，u2是施加到弹性附件上的控制量是模态振型函数，qi（t）是模态坐标，

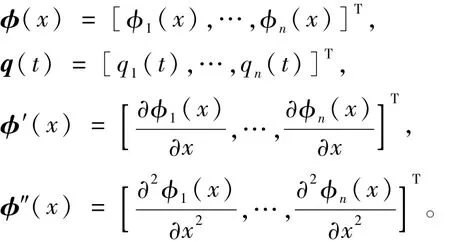
2.2 大角度快速机动的特征建模

关于特征模型的具体定义可参见文献［13］，这里研究式（1）和式（2）的特征建模问题。

定理1.对可用动力学模型式（1）和式（2）描述的被控对象，在满足一定采样周期 Ts的条件下，当要实现位置保持或位置跟踪控制时，其特征模型可用下面的二阶慢时变差分方程概述：

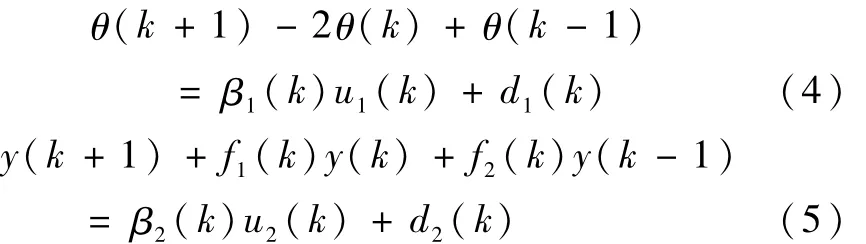
其中，fi，βi（i=1，2）定号、有界，且范围已知，di（i=1，2）有界。

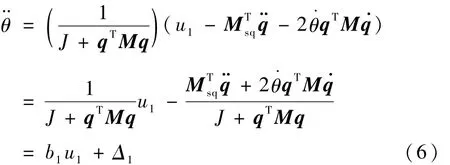
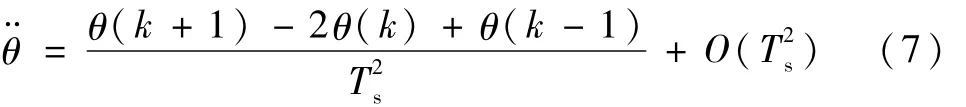
其中Ts是采样周期。在每一采样时刻的离散化过程中假设微分方程式（6）的系数变化可以忽略（当采样周期充分小且控制量有界时，这种处理带来的误差是很小的，可以归结到特征模型的动态建模等价误差项中），将式（7）代入式（6），得到特征模型

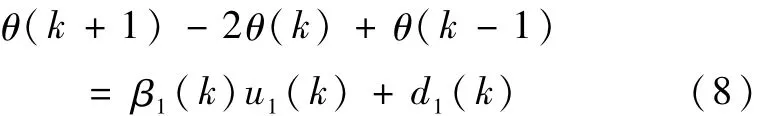
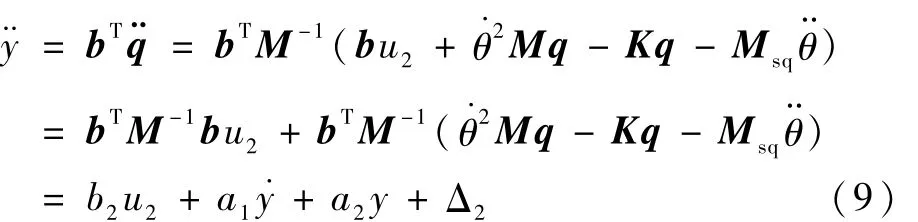
对输出y=bTq求二阶导数，得到可见系统的测量输出y可以用一个带等价干扰的二阶时变微分方程描述。式（9）的参数特点为b2＞0，a1＞0，a2＞0，Δ2（0）=0。

利用差分法对式（9）进行离散化，得到特征模型为

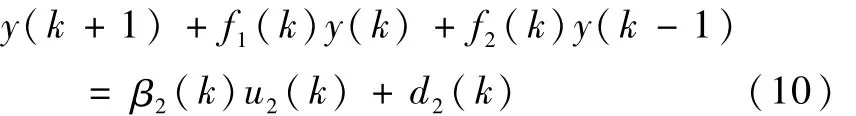
注1.上面特征建模的推导存在一定的近似，但只要采样周期充分小且控制量有界，近似误差就会很小。更严格的证明可以通过差分和积分相结合的方法得到，所得到的特征模型形式与定理1相同。

注2.上述特征模型只有6个特征参数有待辨识，如果不辨识等价干扰项d1和d2，则仅有4个参数需要辨识，极大地减少了待辨识参数的数量。这些参数的一些变化信息可以事先确定并作为先验信息在后面的辨识算法和控制算法中使用。

3 一种基于特征模型的自适应控制方法

3.1 参数辨识算法

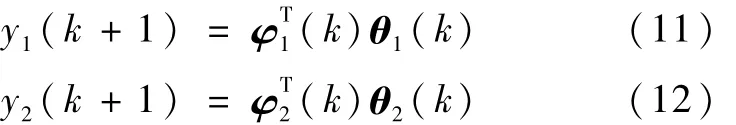
将特征模型式（4）和式（5）简记为其中，y1（k+1）=θ（k+1）-2θ（k）+θ（k-1），φ1（k）=［u1（k），1］T，θ1（k）=［β1（k），d1（k）］T，y2（k+1）=y（k+1），φ2（k）=［y（k），y（k-1），u2（k-1），1］T，θ2（k）=［-f1（k），-f2（k），β2（k），d2（k）］T。

由于要求的控制是机动控制，机动过程中特征参数是时变的，稳态时控制量为0且各特征参数为常值，所以采用遗忘因子渐近至1的最小二乘辨识算法进行参数辨识，如下所示

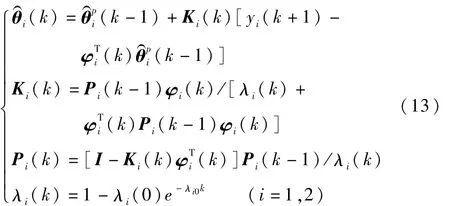
其中，λi0=0.99，λi（0）=0.01。结合关于特征模型的先验信息，可修正用式（13）辨识得到的特征参数的估计值。这里采用的修正方法为Pr（·）是投影算子，它将不在特征参数所在空间的参数估计值投影到参数空间的边界上。

注 3.由于本文对象稳态时 d1（∞）=0，d2（∞）=0，上述辨识算法中也可以不辨识 d1（k）和 d2（k），在动态过程中将其作为衰减干扰看待。由于d1（k）和d2（k）事实上不是独立随机干扰并且控制与辨识相互影响，一般不能保证参数估计有好的性质，采用上面的参数投影对于改善参数估计效果是有益的。

3.2 基于特征参数估计的控制方法

（1）平滑跟踪曲线的设计

设计平滑跟踪曲线的目的在于使控制量不至于过大而进入深度饱和区，同时也有利于减少对弹性模态的激励作用。平滑跟踪曲线 ys=C（s）yr，其中，yr是指令信号，C（s）是一个低通滤波器，满足C（0）=1，其截止带宽及具体形式视具体条件而定。本文采用的滤波器为 C（s）=ω2/（s2+2ζωs+ω2），其中，ζ表示可控制平滑指令曲线的形状，ω表示可控制平滑指令曲线的速度。

（2）控制量的计算

根据式（14）～（17）计算控制量

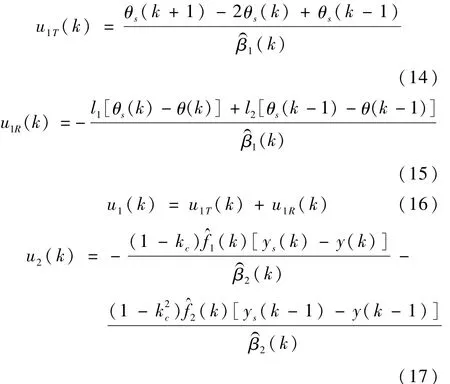
其中，u1T为维持跟踪控制量，u1R为调节镇定控制量，是控制器的设计参数。

3.3 闭环稳定性分析

这里对基于式（5）的自适应控制的闭环系统稳定性做启发性的定性分析。假设式（5）中的等价干扰项d2对闭环稳定性的影响可以忽略不记，则仅需研究特征模型式（5）在控制器式（17）下的指数稳定性条件。进一步假设 p=β2（k）/)β2（k）是慢时变的（可以通过对估计值)β2（k）进行处理得到保证），则根据慢时变系统的指数稳定性定理，可用冻结系统的指数稳定性来研究慢时变系统的指数稳定性。利用朱利判据可以判断冻结系统的指数稳定性。根据这种分析，这里给出当采样周期 Ts趋于0时，参数p以及kc在不同取值下的闭环系统稳定性，结果如图2所示（实线以下的部分表示系统指数稳定，实线以上的部分表示闭环系统不稳定）。

从图2可知，当0.9≤kc＜1时，为保证闭环系统指数稳定，可以容忍的辨识误差是很大的，当然这是以牺牲一部分控制性能为代价的，实际中kc的选取可根据问题需要在鲁棒稳定性和控制性能之间做折中选取。

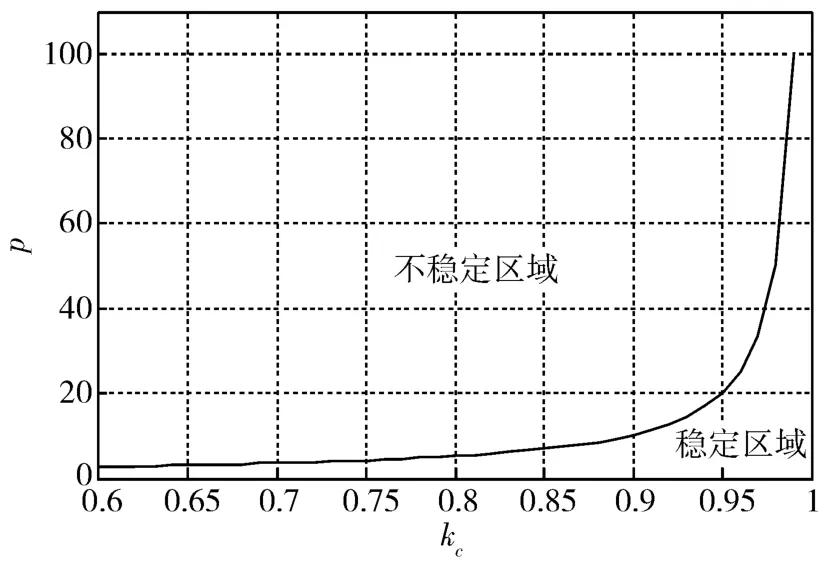
图2 闭环系统稳定性与辨识误差和控制器参数的关系

4 数学仿真

4.1 仿真内容及仿真条件

本节通过仿真来研究所给出的自适应控制方法在柔性航天器大角度快速机动控制中的效果。在仿真中选取采样周期为0.2 s。为了对仿真结果有直观认识，将自适应控制的仿真结果与式（18）和式（19）描述的姿态角PD控制的控制仿真结果进行对比

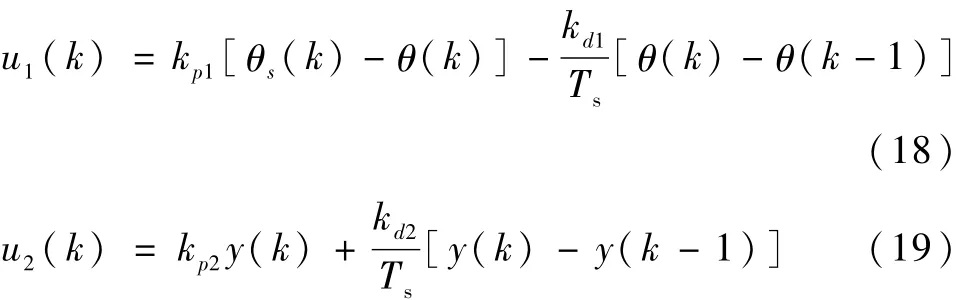
在仿真中假定被控对象中心刚体的惯量参数发生了较大的变化（仿真中取三组惯量参数Jhi（i=1，2，3）），控制要求为将系统从0初始状态控制到姿态角为1 rad且其余状态为0的目标状态。

仿真中对象模型参数为：L=10 m，rA=0.5 m，n=2，EI=400 N·m，ρA=3 kg/m，Jh1=600 kg·m2，Jh2=390 kg·m2，Jh3=300 kg·m2。

仿真中控制器参数为：l1=1.71，l2=-0.74，kc=0.95，Ts=0.2 s，kp1=500，kd1=2500，kp2=5，kd2=10。

4.2 仿真结果及分析

图3～图6是本文控制方法和PD控制方法在被控对象中心刚体惯量取不同值时的仿真结果。

从仿真结果可知，当对象的中心体惯量为Jh1=600 kg·m2时，自适应控制取得了比PD控制更小的跟踪误差；由图4的仿真结果可知，当对象的中心体惯量变化为 Jh2=390 kg·m2时，自适应控制仍取得了比PD控制更小的跟踪误差；由图5的仿真结果可知，当对象的中心体惯量变化为 Jh2=390 kg·m2时，自适应控制的控制量平滑过渡到稳态控制量，而PD控制的控制量则出现了明显的抖动；由图6的仿真结果可知，当对象的中心体惯量变化为Jh3=300 kg·m2时，自适应控制的姿态机动控制性能出现了较明显的下降，但姿态角仍调节到目标值，此时采用PD控制的姿态角则出现发散。

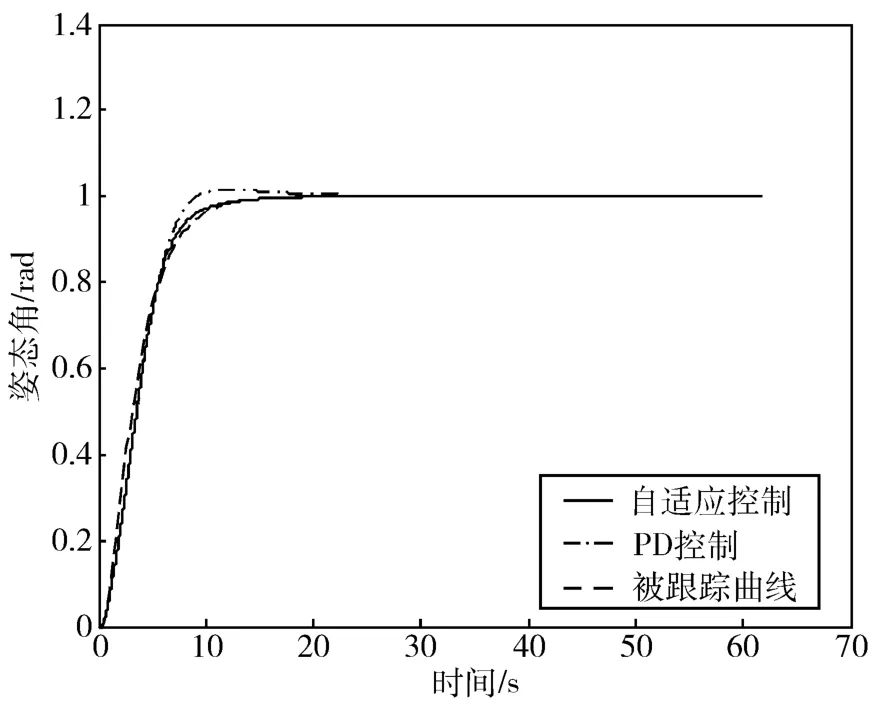
图3 Jh1时的姿态机动控制效果

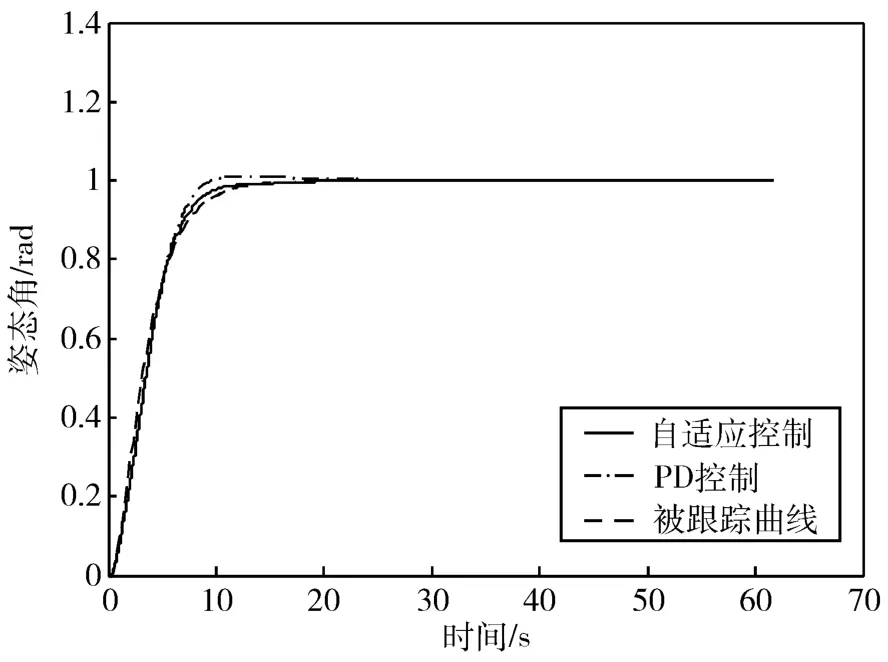
图4 Jh2时的姿态机动控制效果

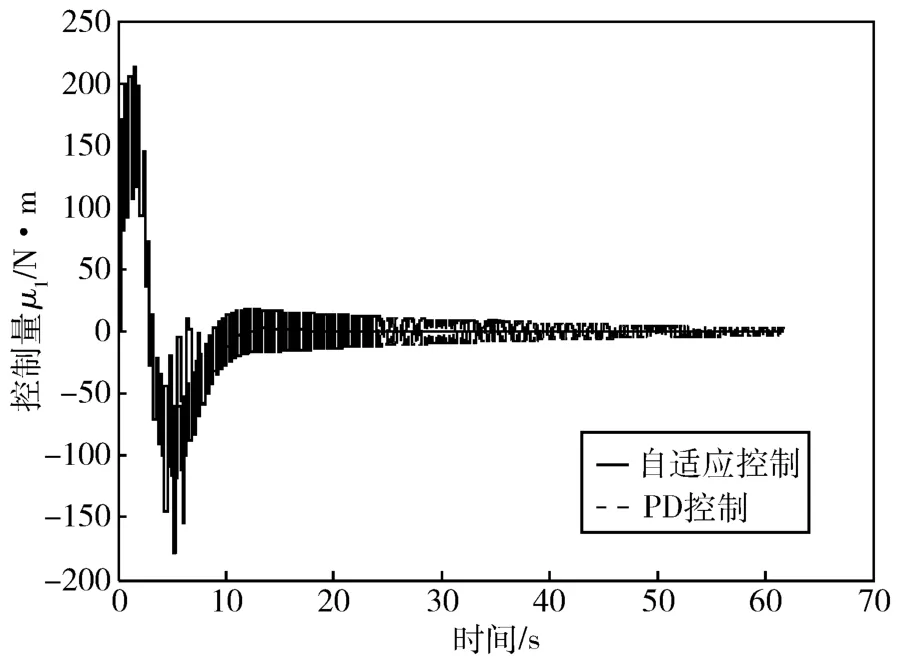
图5 Jh2时的控制量

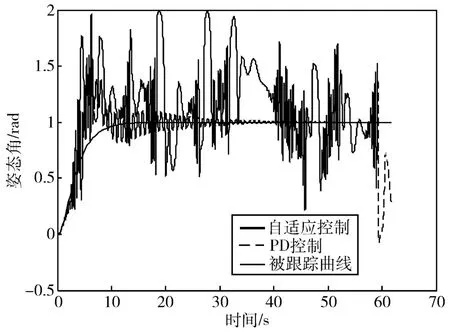
图6 Jh3时的姿态机动控制效果

表1给出了本文提出的自适应控制方法和PD控制方法在不同仿真条件下得到的控制性能，其中ts的定义为

由以上结果可以看出，本文提出的自适应控制方法比PD控制方法具有更强的参数鲁棒性和更好的鲁棒控制性能。采用本文提出的自适应控制方法达到的姿态角控制性能明显优于PD控制的情况。大量的仿真结果表明：

1）本文设计的控制算法对于控制器参数变化具有很强的鲁棒性。

2）本文设计的控制算法对于对象参数变化具有很强的鲁棒性，当对象仿真参数在很大范围变化时，闭环系统仍稳定，且仍能比PD控制取得更好的控制性能。

表1 仿真结果的比较

5 结 论

本文针对中心刚体带柔性附件的航天器做大角度快速机动控制的问题，根据能够反映柔性航天器大角度快速机动特点的动力学模型，推导并建立了其特征模型，给出了特征模型参数的表达式及辨识算法，设计了一种基于特征模型的自适应控制方法并进行了理论分析和数学仿真研究。结果表明，该自适应控制方法可以实现姿态快速机动控制和弹性附件的快速振动抑制。该自适应控制方法设计简单，对控制器参数变化和对象模型变化具有很强的鲁棒性。

［1］ Junkins J L，Kim Y.Introduction to dynam ics and control of flexible structures［M］.Washington：AIAA Inc.，1993

［2］ Kelkar A，Joshi S.Control of nonlinear multibody flexible space structures［M］.London： Springer-Verlag，1996

［3］ Balas M J.Trends in large flexible structure control theory：fondest hopes， wildest dreams［J］.IEEE Transactions on Automatic Control，1982，27（3）：522-535

［4］ Hyland D C，Junkins J L.Active control technology for large space structures［J］.Journal of.Guidance，Control and Dynam ics，1993，16（5）：801-821

［5］ Nurre G S，Ryan S.Dynamics and control of large space structures［J］.Journal of Guidance，Control and Dynamics，1984，7（5）：514-526

［6］ Sparks D W.Survey of experiments and experimental facilities for control of flexible structures［J］.Journal of Guidance，Control and Dynamics.1992，15（4）：801-816

［7］ Dwivedy S K.Dynamic analysis of flexible manipulators，a literature review［J］.Mechanism and Machine Theory，2006，41：749-777

［8］ Benosman M.Control of flexible manipulators：a survey［J］.Robotica，2004，22：533-545

［9］ Balas G J，Doyle J C.Robustness and performance trade-offs in control design for flexible structures［J］.IEEE Transactions on Control Systems Technology.1994，2（4）：352-361

［10］ Annaswamy A M， Clancy D J.Adaptive control strategies for flexible space structures［J］.IEEE Transactions on Aerospace and Electronic Systems，1996，32（3）：952-966

［11］ Astrom K J，Wittenmark B.自适应控制 ［M］.北京：科学出版社，2003

［12］ 肖建强，章定国.转动刚体上柔性悬臂梁的动力学建模与仿真［J］.机械科学与技术，2005，24（1）：45-47

［13］ 吴宏鑫，刘一武，刘忠汉，等.特征建模与挠性结构的控制［J］.中国科学（E辑），2001，31（2）：137-149

Adaptive Control Method for Fast Attitude Maneuver of Flexible Spacecraft

ZHANG Guoqi1，2，DING Jianzhao1
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

In this paper，the issue on fast attitude maneuver control of a spacecraft with flexible appendix is studied.The characteristic model is derived based on the dynamics model of the spacecraft with flexible appendix.A characteristic model based adaptive control method is proposed which can achieve the fast attitude maneuver and vibration attenuation simultaneously.The controller is simple to design with explicit physical meanings on its design parameters and ease of the controller tuning.Both theoretical analysis and computer simulation show that the method proposed in this paper has good robust stability and robust performance to both varying controller parameters and plant uncertainties.Comparison with the traditional proportional-derivative（PD）control method shows that the adaptive control method proposed is superior to PD control in achieving faster attitude maneuver and vibration attenuation of the flexible spacecraft.

attitude fast maneuver；flexible spacecraft；adaptive control；characteristic model

*国家自然科学基金（60704014）及 973计划（2002cb312205）资助项目.

2008-04-28

张国琪（1978-），男，天津人，博士，研究方向为自适应控制（e-mail：zhang-work@sohu.com）。

V448.2

A

1674-1579（2008）04-0023-05