考虑控制饱和的卫星姿态控制器设计*
2008-10-23吕建婷马广富
吕建婷,马广富,高 岱
(哈尔滨工业大学航天学院,哈尔滨 150001)
1 引 言
在稳定飞行阶段,传统的卫星姿态控制器的设计采用全状态反馈,即同时需要姿态信息和姿态角速度信息的测量,这方面的研究成果有许多[1,2]。在实际的航天工程中,角速率敏感器,尤其是高精度的敏感器,其费用都是相当昂贵的。另外当安装了高精度角速率敏感器时,如果敏感器工作失效,就无法继续得到角速度信息。为降低卫星研制成本,或作为角速率敏感器失效后的备份方法,越来越多的学者致力于研究输出反馈控制方案[3,4]。
另一方面,当系统的控制输入发生饱和时,系统的动态性能降低,甚至导致整个闭环系统的不稳定。此时,如果不考虑饱和问题而设计控制器,闭环系统的渐近稳定性是得不到保障的。近年来,诸多学者针对该问题也提出了许多设计控制器的方法[1~3,5]。
本文首先给出卫星姿态动力学方程以及由MRP描述的运动学方程,在控制饱和限制下,针对卫星姿态稳定问题设计了状态反馈控制和输出反馈控制两种方案。所设计的控制方案,不依赖于卫星的惯量参数,同时通过Lyapunov方法证明了闭环系统的全局渐近稳定性。最后对姿态控制系统进行仿真验证,结果表明了所设计的控制算法是行之有效的。
2 卫星数学模型
刚体卫星姿态动力学方程为[6]
(1)
其中,ω=[ω1ω2ω3]T∈R3为星体相对于惯性空间角速度矢量在本体坐标系中的分量;J∈R3×3为卫星的转动惯量矩阵;u=[u1u2u3]T∈R3是三轴控制力矩矢量;对于∀ζ=[ζ1ζ2ζ3]T∈R3,符号ζ×表示如下的斜对称矩阵
由MRP参数σ描述的刚体卫星姿态运动学方程为:
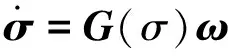
(2)
其中,σ=[σ1σ2σ3]T∈R3,矩阵G(σ)定义如下:
这里I3表示3×3维单位矩阵,并且对于任意的ζ∈R3,定义ζ2=ζTζ。
3 姿态控制器设计

首先给出如下两个引理[7]。
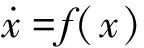
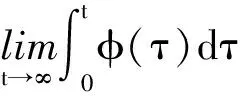
φ(t)→0当t→∞
如下定理给出了实现上述目标的控制方案。
定理1.考虑由(1)、(2)描述的系统,设计状态反馈控制律为
(3)

证明.选取Lyapunov函数
(4)
计算V对时间t的导数,得到:
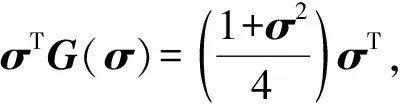
(6)
由于
ξTtanh(αξ)≥0,∀α>0
(7)
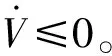
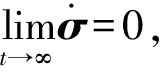
根据矩阵σ的性质及向量函数tanh(cα)的性质
∀c>0
(8)

定理2.考虑由(1)、(2)描述的系统,设计输出反馈控制律为
u=-kpσ-kdGT(σ)tanh(ξ+kσ)
(9)
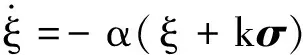
(10)

证明.选取Lyapunov函数
(11)
计算V对时间t的导数,得到
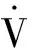
=-kpωTσ-kdωTGT(σ)tanh(ξ+kσ)+
(12)
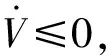
因为
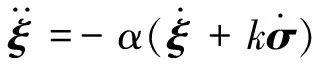
(13)
另外,由控制律(9)容易得到
‖u‖ ≤kp‖σ‖+kd‖G(σ)‖‖tanh(ξ+kσ)‖
(14)
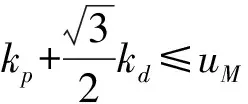
至此,定理2得证。
4 仿真分析
为验证本文提出的姿态稳定控制方法的有效性,选择如下卫星参数进行仿真验证。
卫星的转动惯量为
初始姿态、初始角速率ω分别取为
σ(0)=[0.3 0.2 -0.3]T
ω(0)=[0 0 0]T(rad/s)
考虑定理1提出的控制器,控制器参数选取为
um=0.2,kp=0.1,
λ=200,kd=0.2。
仿真结果如图1~3所示,卫星姿态、姿态角速度和控制输出力矩变化曲线分别如图1、2和3所示。由图可以看出,控制方案能在有限的控制力矩限制条件下能够保证闭环系统的全局渐近稳定性,能很好的完成姿态控制任务。

图1 MRP变化曲线
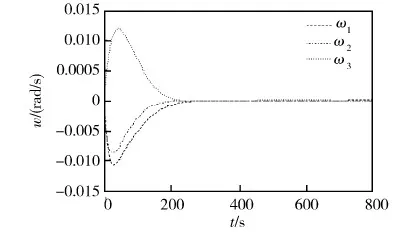
图2 角速度变化曲线
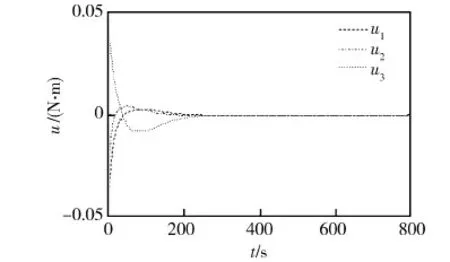
图3 控制量变化曲线
考虑定理2提出的控制器,控制器参数取为
um=0.8,kp=0.1,kd=0.6,
k=25,α=0.1。
卫星姿态、姿态角速度和控制输出力矩变化曲线分别如图4、5和6所示。由图可以看出,在无需角速率反馈的情况下,所提出的控制方案也可以在有限的控制力矩限制条件下较好地完成姿态控制任务。
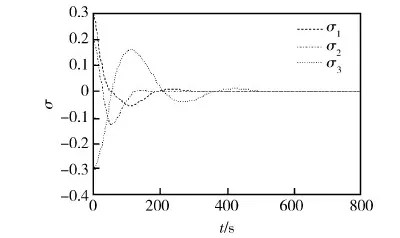
图4 MRP变化曲线
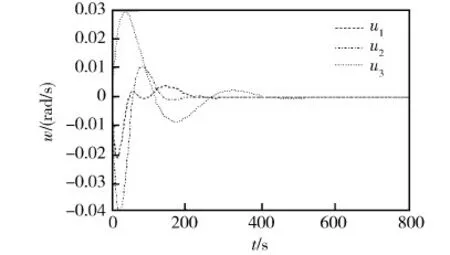
图5 角速度变化曲线
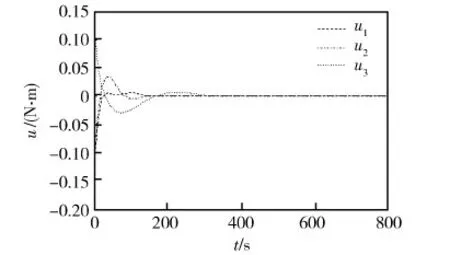
图6 控制量变化曲线
由以上结果可知,通过数学仿真,分别针对定理1和定理2描述的控制方案进行验证,结果表明了所提出的状态反馈和输出反馈姿态控制方案是可行的和有效的。
5 结 论
本文针对刚体卫星的姿态稳定控制设计了状态反馈和输出反馈控制器。针对姿态控制中控制输入饱和问题,本文通过引入双曲正切函数并利用MRP参数自身的性质很好地抑制了控制力矩的饱和问题。仿真结果表明所设计的控制方案很好地实现了姿态控制,保证了闭环系统是全局渐近稳定的。
