形式验证中ROBDD变量排序算法的研究
2008-10-23杨孟飞
王 青,杨孟飞
(1.北京控制工程研究所,北京 100190;2.中国空间技术研究院,北京 100081)
1 ROBDD的概念
目前我国空间技术领域的数字系统设计正在向可编程片上系统(SOPC,System On Programmable Chip)方向发展,而利用形式验证技术提高设计质量、缩短SOPC开发周期是解决验证瓶颈的有效途径。ROBDD (Reduced OBDD)是形式验证算法中最基本的数据结构,而它的状态空间爆炸危机却严重影响着形式验证的适用规模。因此,研究ROBDD的优化方法,对推广形式验证在空间数字系统设计领域的应用有着重要的意义。
1978年,Akers提出了BDD (Binary Decision Diagram) 的概念,它是香农展开定理的图形表示,与其他的布尔函数表示法相比,BDD可以占用较小的存储空间。1986年,R.E.Bryant在OBDD (Ordered BDD) 的基础上,又提出了ROBDD。目前,ROBDD在形式验证、FPGA (Field Programmable Gate Arrays)、CAD (Computer Aided Design)等领域的应用十分广泛[1]。
定义1.BDD是一个具有有限个节点的有根无环图G=
定义2.OBDD是一个满足以下条件的BDD:对于任意两个节点v和v′,如果index(v) < index(v′),那么节点v一定位于节点v′的上方。
定义3.ROBDD是一个满足以下条件的OBDD:对于任意节点v∈V,不会存在low(v)=high(v);对于由任意两个节点v,v′∈V 作为根节点构成的BDD子图,不存在同构。
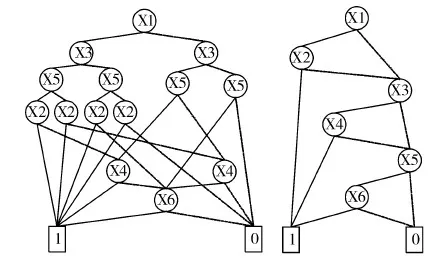
图1 布尔函数f的ROBDD表示
虽然ROBDD在布尔函数的表示和运算方面相当有效,但当它处理大规模设计时,ROBDD的节点仍然太多,会占用大量的存储空间。如果没有一个好的变量排序,那么ROBDD的节点数甚至会成指数倍增长,造成存储空间爆炸问题。如图1所示,对于布尔函数f(x1,x2,x3,x4,x5,x6)=x1x2+x3x4+x5x6,变量排序(x1,x3,x5,x2,x4,x6)构成的ROBBD共有14个非终节点,而变量排序(x1,x2,x3,x4,x5,x6)构成的ROBBD却只有6个非终节点。因此,优化ROBDD的变量排序是解决状态空间爆炸危机最有效的途径。
2 CUDD遗传排序算法的研究[2]
对于一个由N个变量组成的布尔函数,它共有N!种不同的变量排序。如果要寻找最优的变量排序,那么就需要生成所有可能的排序,然后再寻找节点数最少的ROBDD,而这种运算的复杂度是O(N!2N),其中N!代表所有可能的排序,2N是针对每个变量排序构建ROBDD所花费的时间[3]。显然,即使是对于中等数量的变量,极高的复杂度也注定它难以实现。因此,为了避免ROBDD状态空间爆炸的危机,只能采取试探的方法来寻找变量的最优排序。
目前,常用的ROBDD的变量排序算法主要有滑动变量排序算法、煺火变量排序算法、遗传变量排序算法和精准变量排序算法。对于各种ROBDD变量排序算法的评价,主要取决于nodes和time两项指标。其中,nodes是指对设计对象进行变量排序处理后,表示该设计所需的ROBDD节点数;time是指对设计对象进行变量排序处理需要花费的时间。
SMV(Symbolic Model Verifier)是由CMU(Carnegie Mellon University)和IRST(Istituto per la Ricerca Scientifica e Tecnolgica)联合开发的第一个基于ROBDD的符号模型检验系统,它可以对用smv语言描述的设计进行形式验证。为了促进对形式验证方法的研究,SMV的源代码已经完全公开,目前公布的最新版本是NuSMV-2.4.0。NuSMV-2.4.0包含了一个CUDD(CU Decision Diagram Package)数据包,该数据包提供了关于ROBDD的各种操作函数,同时还包含了滑动变量排序算法、煺火变量排序算法、遗传变量排序算法和精准变量排序算法的功能。表1就是对这四种算法性能的比较,其实验环境为Pentium 4 处理器,1.9GHZ主频,512M内存,实验工具为符号模型检验工具NuSMV-2.4.0自带的cudd-2.3.0.1数据包。通过对由21个变量组成的布尔设计进行变量排序后,各种算法生成的ROBDD节点数如表1所示。
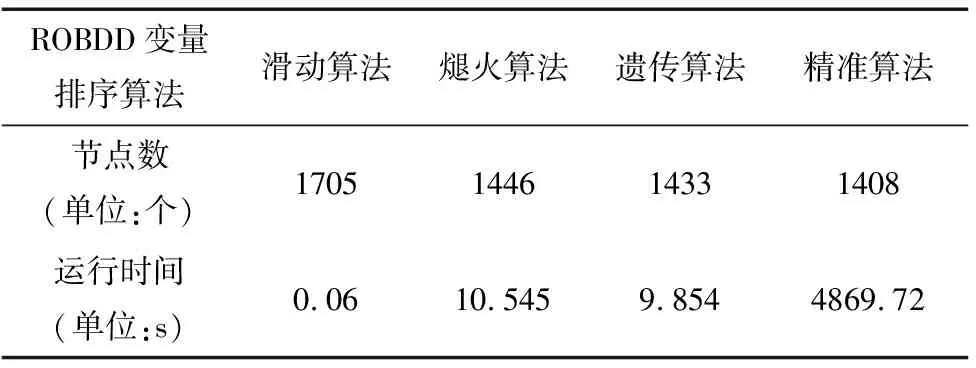
表1 各种变量排序算法的比较
显然,在一般情况下,各种变量排序算法都很难在节点数和运行时间两项指标内得到平衡。精准算法的优化效果最佳,但是它的运行时间却难以接受;滑动算法的运行时间最短,而优化的结果却并不理想;虽然遗传算法和煺火算法的运行时间比较接近,但是前者的优化结果却较为优异。因此,研究并改进CUDD遗传变量排序算法,使它在可以容忍的运行时间内产生更优的排序结果,是缓解状态空间爆炸危机的有效途径之一。
遗传算法的思想GA(Genetic Algorithm)起源于20世纪60年代,经过30多年的发展,GA取得了丰硕的应用成果和理论研究进展[4]。遗传算法效仿了生物界的优胜劣汰原则,是一种基于随机搜索的自动优化技术。cudd-2.3.0.1数据包中使用的遗传排序算法操作流程如图2所示,它是通过CUDD数据包中的genetic.c文件中的cuddGa函数实现的。在该设计中,一个个体就是一种变量排序,而组成这个个体的基因就是布尔变量。每个个体的适应值等于根据该排序产生的ROBDD节点数,节点数越少适应度就越高,结束算法的优化判断准则是世代数超过60。cuddGa函数在选择操作中,使用了轮盘赌选择法(roulette wheel selection)选择再生个体,交叉操作使用了部分匹配交叉(PMX:Partially Matched Crossover)。
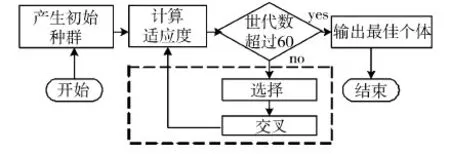
图2 CUDD遗传排序算法的操作流程图
本文对CUDD包中遗传排序算法的改进主要体现在两个方面:首先,在交叉运算后增加了变异操作,选择的变异算法是二次交换;其次,在种群的世代更新中,增加了保留最优个体的操作。改进后的cudd遗传排序算法操作流程如图3所示。
(1)二次交换的变异操作
选择、交叉和变异是三种最基本的遗传操作,而CUDD包中的cuddGa函数只考虑了选择和交叉两种操作,这会造成遗传算法的局部收敛,难以得到全局的最优解。与生物界的近亲繁殖影响进化历程类似,种群的个体数是有限的,经过若干代的交叉操作,源于一个较好祖先的子个体将会逐渐的充斥整个种群,使得问题过早收敛。

图3 改进后的CUDD遗传排序算法操作流程图
为了避免这种现象,应该在进化的过程中加入新遗传基因的个体,即增加变异操作。变异操作有利于保持种群个体的多样性,避免最优解的局部收敛性。理论研究表明,这种由选择、交叉和变异三种基本操作组成的改进遗传算法,其遗传搜索过程完全符合齐次马尔科夫随机过程准则[5]。在改进的遗传变量排序算法中,本文使用了二次交换作为变异操作的实现算法。
1)为种群中所有的个体设定个体变异概率;
2)根据个体变异因子选择变异个体individual;
3)随机选择individual中的两个变异基因位置gene1和gene2;
4)交换gene1位置和相邻位置的变量;
5)交换gene2位置和相邻位置的变量;
6)保留新生成的个体individual′;
7)用新生成的个体individual′替代个体individual,更新当前种群。
二次交换的变异操作步骤如上所示,其中个体变异因子设置为0.1,而对于变异个体的选择则使用了轮盘赌选择法,由于适应度高的个体发生变异的概率也高,因此,这种对较优个体进行变异的操作避免了排序解的局部收敛。改进算法中对变异基因的选择使用了完全随机选择法,而二次交换的操作增加了种群的多样性。
(2)保留最优个体的世代繁殖
由于变异操作的存在,在世代的繁殖过程中,当前种群中的最优个体有被破坏的可能。为了避免当前种群中的最优个体发生变异,改进的遗传算法中采用了保留最优个体的世代繁殖操作。另外,研究表明改进前的CUDD遗传排序算法并不是全局收敛的,而改进后的基于精英保留策略的遗传算法却具备了全局收敛性[6]。
cuddGa函数为种群中的所有个体都分配了自己的地址空间,其坐标范围是[0,popsize+1],其中0到popsize-1保存了当前种群中的popsize个个体,popsize和popsize+1保存了交叉操作后产生的两个子个体,而popsize是指种群的大小,即种群中包含的个体数目。在改进后的算法中又单独申请了一份地址空间popsize+2,在该地址空间内保留了世代繁殖过程中的最优个体。这种保留最优个体的世代繁殖过程如图3所示,其中“更新世代间最优个体”的操作过程是通过以下步骤实现的。
1)计算当前种群中所有个体的节点数目,选择节点数目最少的个体作为最优个体individual;
2)比较individual和individual_best的性能,如果individual的节点数小于individual_best,那么将individual_best更新为individual,并存入popsize+2地址空间;
3)世代数增1,进行种群的繁殖,即选择、交叉和变异。
算法中的individual_best是预先存入popsize+2的上一代最优个体,它可以通过以上操作在世代繁殖中不断地得到更新,作为最终的结果输出。

表2 CUDD遗传排序算法改进前后的性能比较
改进的CUDD遗传变量排序算法是用C语言设计实现的,其中二次交换的变异操作通过子函数my_mutation()完成,而保留最优个体的世代繁殖操作是直接在cuddGa()主函数中设计完成的。改进后的CUDD遗传排序算法函数仍然是CUDD数据包的组成部分,通过cygwin环境对CUDD数据包和NuSMV工具设计文件的编译,最终可生成NuSMV.exe可执行文件,用于对改进后的CUDD遗传变量排序算法验证。
3 改进遗传排序算法的验证
为了验证改进后遗传排序算法的性能,本文使用SMV语言进行了各种规模的设计,并在NuSMV-2.4.0验证平台上完成了测试。实验中比较的性能参数有三项:nodes是指ROBDD的节点数;time是指运行算法花费的时间,单位是秒;average是指种群中个体的平均节点数。其中nodes,time,average是CUDD包中原有遗传排序算法的性能指数,而nodes′,time′,average′是改进后的CUDD遗传排序算法性能指数。
通过对实验数据的分析,可以得到以下几点结论:
1)参考nodes指标可以说明,改进后的算法可以获得更少的ROBDD节点数,而且设计规模越大,节点数的缩减幅度越大。
2)参考time指标可以说明,改进后的算法在时间复杂度仍然优于exact算法,运行时间的增长幅度可以接受。
3)参考average指标可以说明,改进后的算法提高了个体的平均适应度,优化了种群的性能。
4 结 论
本文通过对遗传变量排序算法的研究,对CUDD数据包中的cuddGa设计进行了改进,改进后的算法中增加了二次交换变异操作和保留最优个体的世代繁殖内容。实验数据表明,改进后的CUDD遗传变量排序算法能够在可以容忍的时间增幅内进一步优化ROBDD结果,减少了ROBDD节点的数目,在一定程度上缓解了状态空间爆炸的危机。
