挠性卫星轨控期间动力学与姿态控制*
2008-10-23刘莹莹
刘莹莹,周 军
(西北工业大学精确制导与控制研究所,西安 710072)
1 引 言
卫星进行轨道调整期间,轨道控制推力会激起卫星挠性附件的振动,从而影响卫星的质心运动与姿态运动,引起卫星轨道与姿态运动的耦合。
目前人们对挠性卫星的动力学建模与控制开展了大量研究,对于带有大型挠性附件的卫星动力学问题已经比较清楚。但是主要研究集中在多体动力学建模方法[1~4],挠性振动对卫星姿态的影响[2,5]以及带有挠性附件的航天器姿态控制方面[6~8]。对于卫星轨道控制期间,推力对挠性振动、姿态运动的耦合影响讨论得很少。
本文针对卫星轨道控制推力对挠性太阳帆板振动的影响问题,利用伪坐标Lagrange方程[1,2],建立了系统动力学模型,分析了卫星质心运动、姿态运动与挠性振动的耦合关系。考虑姿态控制推力器开关输出特性,设计了轨控期间姿态控制律。通过数学仿真验证了轨控推力对挠性帆板的激振影响,以及对卫星姿态的影响,验证了轨控期间姿态控制方案的可行性。
2 挠性卫星运动学描述

图1 卫星坐标系示意图
带有大型挠性太阳帆板的卫星结构示意图如图1。在卫星轨道控制期间,太阳帆板以某固定角度相对卫星本体锁定。设OXoYoZo为卫星轨道坐标系,O为卫星质心,OXo指向卫星运行前进方向,OYo为轨道负法向方向,OZo指向地心;OXbYbZb为卫星本体坐标系,各轴固连于星体;OfXfYfZf为帆板坐标系,Of位于帆板与中心刚体连接处,各轴与帆板未形变状态固连。
卫星轨道坐标系与本体坐标系按3-1-2顺序旋转ψ、φ、θ三个欧拉角,转换矩阵为:
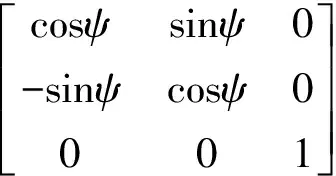
(1)
卫星相对惯性空间角速度ω为:
(2)
轨控期间帆板与本体固连,设帆板坐标系方向与本体坐标系方向一致。
定义如下向量:R0为地球中心到卫星质心的向量;Vo为卫星质心速度矢量;rb为卫星质心到星体质量元向量;ω为卫星相对惯性空间角速度;rof为卫星质心到帆板与本体连结点Of向量;rf为Of到帆板质量元未形变时的向量;u为帆板质量元形变位移,u=Φq(t),其中Φ为帆板振型,q(t)=[q1q2…qN]T为模态坐标,N为模态阶数。则卫星刚体部分任一质量元的速度矢量为:
(3)
帆板上任一质量元的速度矢量为:
(4)
3 系统动力学模型
卫星由中心刚体与太阳帆板组成,利用伪坐标Lagrange方法建立系统动力学模型。
计算得到卫星刚体部分动能为:
(5)
其中mr为刚体部分总质量,Ir为刚体部分惯量张量,ror为星体质心到刚体部分质心的向量。
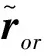
设卫星姿态角速度与挠性振动均为小量,略去高阶小量,帆板部分动能为:
(6)
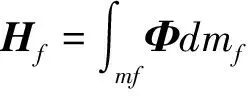
帆板弹性势能为:
(7)
ωfi(i=1,2,…N)为帆板第i阶固有频率。
考虑帆板的振动阻尼,
(8)
ξf为阻尼系数。
得到系统Lagrange函数:
L=Tr+Tf-Uf
(9)
考虑到O为卫星质心,则mrror+mf(rof+rf1)=0,经计算,得到系统动力学方程:
(10)

(11)

(12)
其中:
mt=mr+mf为卫星总质量;

F、M为外力系向O点简化得到的主矢量与主矩,Qq是对应于广义坐标q的广义力。
4 轨控推力的影响分析

当卫星进行轨道调整时,轨道控制推力器工作,对卫星产生推力,通过质心运动与帆板振动的耦合,将激起帆板振动,并且通过帆板与姿态的耦合影响姿态运动。
帆板与卫星本体连接位置为rof=[0,-1,-0.7]m。帆板振动频率与振型由有限元方法分析得到。根据挠性模态截断准则,本文取帆板前五阶振动模态,振动频率分别为0.1Hz、0.38Hz、0.45Hz、0.7Hz、0.8Hz,其中第一、三、五阶为弯曲振动,第二、四阶为扭转振动。振动阻尼系数取0.005。由帆板振型计算得到:
耦合系数矩阵Cv中的第一列表示帆板一阶振型对卫星三维质心运动的耦合影响,以此类推,每一列表示某阶振型对质心运动的耦合影响;矩阵中的一行表示各阶振动对某一方向质心运动的耦合影响。同样,耦合系数矩阵Ca中的第一列表示帆板一阶振型对卫星三轴姿态运动的耦合影响,矩阵中的一行表示各阶振动对某一通道姿态运动的耦合影响。
因此,帆板弯曲振动(第一、三、五阶) 主要影响X、Y方向的质心平动,以及绕Z方向的姿态运动,即偏航姿态;帆板扭转振动(第二、四阶) 主要影响Z方向质心平动,以及绕X、Y方向的姿态运动,即滚动、俯仰姿态。
5 轨控期间姿态控制方案
轨道调整期间,轨道控制推力会激振挠性帆板,从而影响卫星姿态。并且由于推力偏心,会产生较大的常值干扰力矩直接改变卫星姿态。因此轨控期间采用推力器执行机构进行姿态控制,提供较大的控制力矩,克服轨控推力偏心产生的干扰,保持卫星姿态角、角速度在一定范围内。
由于推力器的不连续输出特性,可以采用变结构控制、斜开关控制等非线性控制方法,使姿态进入极限环稳定方式。限于篇幅,本文姿态控制采用简单的三通道独立设计,以俯仰通道开关控制方法为例,控制律如下:
(13)


6 轨控期间动力学与控制仿真分析
6.1 轨控期间动力学特性分析
本文分析的卫星参数为:整星质量mt=2000kg,整星转动惯量I0t=diag(3700,4500,6000)kg·m2。
轨道控制推力器连续300s产生10N常值推力。首先考察轨道控制推力过整星质心,且推力方向沿卫星本体X轴正向的情况。暂不考虑推力偏心产生干扰力矩对姿态与挠性帆板的影响,推力对帆板的激振情况如图2,给出了帆板前三阶挠性振动与卫星本体相对轨道坐标系的角速度,帆板四、五阶挠性振动较小,仿真图略。由仿真结果可知:
(1) X方向轨控推力主要激起帆板一阶弯曲振动,对高阶挠性振动的影响较小。考虑阻尼,帆板各阶振动在自身阻尼作用下逐渐收敛。
(2) 在轨控常值推力作用下,q1,q3与q5趋近常值,说明常值推力作用下帆板有常值挠性形变。
(3) 帆板振动会引起卫星本体姿态的振动,在这种情况下,帆板振动主要引起卫星偏航姿态ω2的振动,对滚动、俯仰姿态影响较小。
因此,轨道控制推力会激起挠性帆板振动,该振动也会影响卫星本体姿态运动。

图2 轨控期间卫星动力学
6.2 轨控期间姿态控制方案仿真分析
轨道控制推力仍然连续300s产生10N常值推力,推力方向沿卫星本体X轴正向,并且考虑轨道控制推力不过整星质心,产生干扰力矩为[0 0.25 0.1]TN·m,在姿态控制力矩作用下,卫星姿态与挠性振动如图3。给出了帆板前三阶挠性振动以及卫星本体姿态角、姿态角速度相平面图,高阶挠性振动较小。由仿真结果可知:

图3 轨控期间姿态控制曲线
(1) 轨道控制推力仍然主要激起帆板一阶挠性振动,并引起偏航姿态振动。姿态控制力矩也会影响帆板挠性振动,偏航控制力矩(图略)主要影响帆板一阶振动,俯仰控制力矩(图略)主要影响二阶振动。
(2) X方向轨控推力对滚动通道不产生干扰力矩,并且挠性振动对滚动通道的影响也较小,因此在300s仿真时间内滚动通道姿态角度、角速度保持较小。


因此,考虑轨控推力产生的干扰力矩,以及挠性振动影响,卫星在控制力矩作用下,能够进入期望的极限环,工质消耗较小,控制精度达到轨道控制期间的要求。
7 结 论
本文研究了卫星轨道调整期间,轨控推力对卫星帆板振动以及卫星姿态的影响。根据推力器输出特性,设计了轨道机动期间卫星姿态控制律。主要结论如下:
(1) 卫星轨道调整期间轨控推力会激起帆板振动,并且影响卫星姿态运动;
(2) 考虑轨控推力偏心产生的干扰力矩,以及挠性振动影响,卫星在姿态控制推力器作用下,三轴姿态都能够进入期望的极限环,控制精度满足轨道机动期间的要求。
