三角形全等的常见模式

韩　霞

三角形全等是图形全等的基础，也是初中数学学习的重点之一．为了帮助同学们学好三角形全等，笔者总结出三角形全等的六种常见模式．

一、“公共角”模式

公共角是两个图形中都含有的角，为全等提供了一个自然条件．在判断全等时，可以考虑与角有关的判定方法．

例1如图1，AB=AC，AD=AE，请说出∠B=∠C的理由．

解析：图中的∠A是公共角，再加上AB=AC，AD=AE，则△ABD≌△ACE（SAS）.全等三角形的对应角相等，所以∠B=∠C.

二、“对顶角”模式

“对顶角相等”为判断三角形全等提供了一个自然条件．这时，可以考虑与角有关的判定方法．

例2如图2，OA=OB，OC=OD.试问：AC∥DB吗？

解析：∠AOC和∠BOD是对顶角，又因为OA=OB，OC=OD，所以△AOC≌△BOD（SAS），所以∠C=∠D.内错角相等，两直线平行，因此，AC∥DB.

三、“公共边”模式

公共边相等是两个三角形全等的一个自然条件．

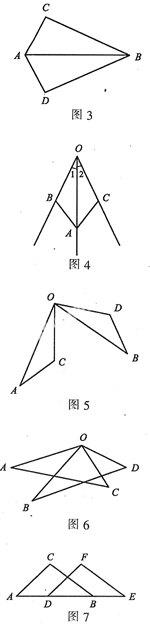
例3如图3，AC=AD，BC=BD.AB是∠CAD的平分线吗？

解析：由于AC=AD，BC=BD，考虑到AB是公共边，所以△ABC≌△ABD（SSS），所以∠CAB=∠DAB，AB平分∠CAD.

四、“角平分线”模式

角平分线提供了两个角相等，同时，角平分线又可以成为公共边，因此有角平分线的问题应考虑SAS或AAS或ASA的判定方法．

例4如图4，OA平分∠BOC，并且OB=OC，请指出AB=AC的理由．

解析：因为OA平分∠BOC，所以∠1=∠2.又已知OB=OC，再由于OA是公共边，所以△OAB≌△OAC（SAS），所以AB=AC.

五、旋转模式

如图5，△OAC绕点O逆时针方向旋转角α（∠AOB=∠COD=α）就到了△OBD的位置.这类问题常用SAS证明．需要利用“等角+公共角=公共角+等角”的思路解题.比较难的题中往往有这种全等的模式.

例5如图6，OA=OB，OC=OD，∠AOB=∠COD，请说明AC=BD的理由．

解析：∠AOB+∠BOC=∠COD+∠BOC，即∠AOC=∠BOD.再因为OA=OB，OC=OD，所以△OAC≌△OBD（SAS），所以AC=BD.

六、平移模式

把全等三角形沿某边所在直线平移，便把对应边都分成了两部分，这时往往通过两条线段加上或减去同一线段的方法得到对应边相等．

例6如图7，AC=DF，BC=EF，AD=EB，请说明∠C=∠F的理由．

解析：AD=EB，所以AD+DB=DB+EB，即AB=DE.再考虑到AC=DF，BC=EF，便可得到△ABC≌△DEF（SSS），所以∠C=∠F.