轴对称问题“错解集中营”

张海生

在轴对称问题中，容易出现这样或那样的错误，本文中作者想通过几个例题简单分析一下同学们出现的几个“小错误”，以期帮助同学们找出错误原因，在解题时避免类似的问题发生.

一、混淆轴对称与轴对称图形概念

例1图形成轴对称和轴对称图形是同一个概念吗？

错解：轴对称与轴对称图形是一回事，都是关于某条直线对称．

错解分析：产生上述错误认识的原因显然是对轴对称与轴对称图形这两个概念的含义未能正确理解．（1）轴对称反映的是两个图形之间的形状和位置关系，而轴对称图形是指一个图形自身的性质；（2）轴对称的对称点分别在两个图形上，而轴对称图形的对称点都在同一个图形上．当然，如果把轴对称图形沿对称轴分成两部分，那么这两部分关于这条对称轴成轴对称；如果把两个成轴对称的图形看成一个整体，那么它就是一个轴对称图形．

正确解答：轴对称和轴对称图形是两个不同的概念，但这两个概念之间又有着密切的联系．（1）“轴对称”是“关系”，“轴对称图形”是“图形”．（2）通常说“某两个图形关于某直线对称”或“某两个图形成轴对称”，“某一图形是轴对称图形”．（3）两概念的联系点是：“某两个图形成轴对称”是指沿一直线折叠，直线两边的两个图形重合，轴对称图形是指一个图形在这条对称轴两边的两部分重合．

二、错将轴对称与全等画等号

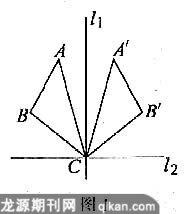
例2如图1，判断△ABC与△A′B′C的关系．

错解：△ABC和△A′B′C对称．

错解分析：说两个图形对称，必须说它们关于哪条直线对称．在图1中，△ABC和△A′B′C关于直线l2不对称．实质上，全等只是从图形的形状相同、大小相等两个方面揭示了两个图形的关系，而轴对称是从形状相同、大小相等、位置关于某条直线对称三个方面揭示了两个图形的关系．

正确解答：△ABC和△A′B′C关于直线l1对称．

三、漏找、错找轴对称图形的对称轴

例3求线段、角、等腰三角形、正方形、圆的对称轴条数．

错解：线段的对称轴有一条，是它的垂直平分线；角的对称轴有一条，是它的平分线；等腰三角形的对称轴有一条，是底边的垂直平分线；正方形的对称轴有两条，是两组对边中点的连线；圆的对称轴有无数条，是它的直径．

错解分析：（1）图形的对称轴是直线，而不是线段；

（2）线段的对称轴有两条，正方形的对称轴有四条，等腰三角形的对称轴有一条或三条．

正确解答：线段的对称轴有两条，是线段的垂直平分线和它所在的直线；角的对称轴有一条，是角平分线所在的直线；等腰三角形的对称轴有一条或三条，是底边的垂直平分线；正方形的对称轴有四条，是对角线所在直线和过对边中点的直线；圆的对称轴有无数条，是过圆心的直线（或直径所在的直线）．

四、关于轴对称与关于直线对称混淆

例4求点P（2，-5）关于x轴对称的点的坐标．

错解：点P（2，-5）关于x轴对称的点的坐标为（-2，-5）．

错解分析：上述错解的产生是因为对于点关于坐标轴对称的点的坐标特点不清楚．

正确解答：点P（2，-5）关于x轴对称的点的坐标为（2，5）．

五、对于无图问题，考虑欠周全，造成漏解

例5等腰三角形一腰上的高与另一腰所成的夹角为45°，求这个等腰三角形顶角的度数．

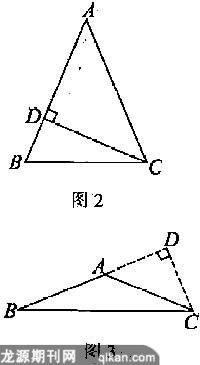
错解：如图2，由题设知，∠ACD=45°，故∠A=45°.

错解分析：就此题而言，等腰三角形一腰上的高既可以在等腰三角形内，也可以在等腰三角形外，需分类讨论．

正确解答：①当高在等腰三角形内部时，如图2，由题设知，∠ACD=45°，故∠A=45°.

②当高在等腰三角形外部时，如图3，由题设知，∠ACD=45°.故∠DAC=45°，故∠BAC=180°-45°=135°.

故此等腰三角形的顶角为45°或135°．