巧构相似三角形 妙证等积式
2008-07-19刘艳丽
刘艳丽
在探求结论是等积式(或比例式)的几何题时,若能根据题设和图形特征,恰当添加辅助线,巧构相似三角形,往往会使得某些看似困难的几何题迅速找到解题途径,现略举几例解析如下.

例1在△ABC中,∠B=2∠C,试说明AC2=AB2+AB·BC.
分析:可将结论变形为AC2=AB(AB+BC),故联想到构造一条长等于AB+BC的线段.如图1,延长AB至D,使BD=BC,连接CD,构成共边共角相似三角形,然后说明△ABC∽△ACD,从而使问题得以解决.
解:如图1,延长AB至D,使BD=BC,连接CD,则 ∠BDC=∠BCD.又∠ABC=∠BDC+∠BCD,所以 ∠ABC=2∠BDC.又∠ABC=2∠ACB,所以∠ACB=∠BDC.又∠CAB=∠DAC,所以△ABC∽△ACD,得到AB∶AC=AC∶AD,故AC2=AB·AD=AB(AB+BD)=AB2+AB·BD=AB2+AB·BC.
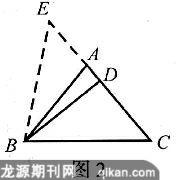
例2锐角等腰△ABC中,AB=AC,BD⊥AC于点D,试说明BC2=2AC·CD.
分析:结论可变形为BC2=AC·(2CD),故联想到构造一条长等于2CD的线段,因此可延长CD至E,使DE=CD,连接BE,构成共边共角相似三角形,然后说明△ABC∽△BEC,从而使问题得解.
解:延长CD至E,使DE=CD,连接BE,如图2.由DE=CD,BD⊥AC,得△BCE是等腰三角形,所以∠C=∠E.又∠C=∠CBA,所以∠CBA=∠E.又∠ACB=∠BCE(公共角),所以△ABC∽△BEC,则BC∶CE=AC∶BC,故BC2=AC·CE=AC·(2CD)=2AC·CD.
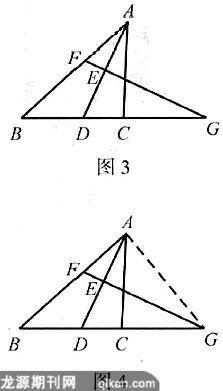
例3如图3,在△ABC中,AD平分∠BAC交BC于点D.FG垂直平分AD,分别交AB、AD及BC的延长线于点F、E、G,试说明DG2=CG·BG.
分析:由于DG、CG、BG三条线段在同一条直线上,它们之间的比例关系难以确定.可考虑将线段转移,等量代换.由于题设中有FG是AD的垂直平分线,所以AG=DG,从而连接AG,如图4,可构成共边共角相似三角形.通过△ABG∽△CAG,可使问题获解.
解:如图4,连接AG.因为FG垂直平分AD,所以DG=AG,且∠ADG=∠DAG.又因为AD平分∠BAC,所以∠BAD=∠DAC.又因为∠BAG=∠BAD+∠DAG,∠ACG=∠DAC+∠ADG,所以∠BAG=∠ACG.又∠BGA=∠AGC(公共角),所以△ABG∽△CAG,从而AG:CG=BG:AG,故AG2=CG·BG,而DG=AG,所以DG2=CG·BG.
例4在等腰梯形ABCD中,AB∥CD,AC是对角线,试说明AC2=AD2+AB·CD.
分析:如图5,要证AC2=AD2+AB·CD,可在AC上适当选择一点P,则AC=AP+PC,若能得到AC·AP=AB·CD,及AC·PC=AD2,两式相加,即可获解.而要得到这两个等式,又要有△ABP∽△CAD及△ABC∽△BPC,因而需要构造相似三角形.以点B为顶点,BA为一边作∠ABP=∠CAD,交AC于点P,可使问题获解.
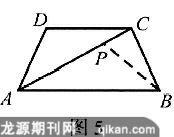
解:如图5,以点B为顶点,BA为一边作∠ABP=∠CAD,交AC于点P.由AB∥CD,得∠BAP=∠ACD,所以△ABP∽△CAD,则AB∶AC=AP∶CD,即AC·AP=AB·CD .①
由等腰梯形ABCD得∠DAB=∠CBA,而∠ABP=∠CAD,所以∠BAC=∠PBC.又∠ACB=∠BCP,所以△ABC∽△BPC.所以AC∶BC=BC∶PC,即AC·PC=BC2.②
①+②,得 AC·AP+AC·PC=AB·CD+BC2.而AC·AP+AC·PC=AC(AP+PC)=AC2,BC=AD,所以AC2=AD2+AB·CD.
例5如图6,△ABC和△ABD在公共边AB的同侧,AC和BD相交于点E,且∠C+∠D=180°,试说明 AB2=AE·AC+BE·BD.
分析:要证AB2=AE·AC+BE·BD,可在AB边上适当选择一点P,则AB=AP+BP.若能得到AE·AC=AB·AP及BE·BD=AB·BP,两式相加,即可获解.而要得到这两个等式,又需有△AEP∽△ABC及△EBP∽△ABD,因而联想到构造相似三角形.
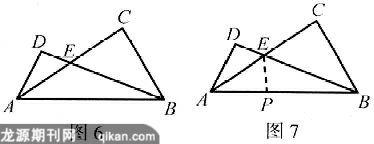
解:以点E为顶点,AE为一边作∠AEP=∠ABC,交AB于点P,如图7.又∠EAP=∠BAC,得△AEP∽△ABC,从而AE∶AB=AP∶AC,即
AE·AC=AB·AP .①
因为∠APE+∠BPE=180°,∠C+∠D=180°,而∠APE=∠C,所以∠BPE=∠D.又∠EBP=∠ABD,所以△EBP∽△ABD,从而BE∶AB=BP∶BD,即BE·BD=AB·BP .②
①+②,得AE·AC+BE·BD=AB·AP+AB·BP=AB(AP+BP)=AB·AB=AB2.
从以上几例可以看出,巧妙构造相似三角形,借助相似三角形的有关性质,可迅速找到解题途径.其解题思想就是:结论需要什么,就设法构造出什么.比如,构造出某角2倍的角,某边2倍的边,某种比例关系式等.
