谈期中总结

作者简介 何荣炎，郑州外国语中学高级教师，河南省学科带头人．河南省教学技能竞赛一等奖，河南省数学竞赛优秀辅导员．在长期的教学实践中，注重思维教学，启发学生的思维．近年来，在转化后进生方面作了有益的尝试，效果明显，先后在《河南教育》《中学生数理化》等杂志上发表了多篇论文．

期中考试日益临近，考前复习要求我们对所学知识加以梳理和消化，形成自己的知识体系．在复习过程中，你注意到以下几个方面了吗？

一、理解课本中的基本概念，注重它们的实际运用

这个要求看上去是老生常谈，实际做好却非常不易，原因是，很多同学只知道概念的表象，却忽略了概念的内涵，还有些同学片面地认为新课标淡化了概念．实际上，课标中更多地渗透了某一知识概念形成的过程，更突出了对概念的理解．因此，你在复习期间，必须加深对基本概念的理解和剖析，注重知识的来龙去脉及它的实际应用．

下面以一元一次不等式为例，具体说明对基本概念的复习．

1．找出课本（本章）内容所包含的知识点（也可以按线索去找）：①不等式；②不等式的基本性质；③不等式的解集；④一元一次不等式；⑤一元一次不等式组；⑥不等式及不等式组的解法、解集的表示方法；⑦不等式的实际应用．

2．理解各个知识点，确定各知识点中的关键字和词，分解剖析，反复推敲，重在与前面所学知识类比，切忌死记硬背．例如，一元一次不等式定义，把握住“元、次、不等式”这几个关键词．此时，再用类比一元一次方程定义的方法，就会很自然地理解这一基本概念，并且找出它与一元一次方程的联系与区别．

3．针对此概念，从课本或教辅书上找出与此内容相关的习题进行练习，即可达到运用的目的．

二、注重知识的纵横联系与交叉，领会常规的数学思想与方法

在掌握和理解基本概念的基础上，更应该注重它与其他知识点的相互联系与区别，这是提升层次的一个关键．

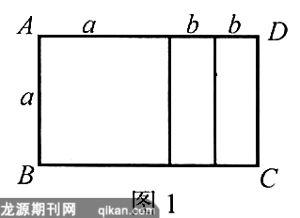
怎样找出知识点的前后联系呢？更多地是用回忆的方法将知识相互联系．例如，学习分解因式时，可以想象与此知识点有联系的知识有哪些，它们的联系方式有哪些，在实际生活中有哪些表现形式等．你很快就能归纳出：①与分式联系在一起，可以进行分式的约分，也可进行通分．②与化简求值联系在一起，可以进行整体代入．③与图形联系在一起，可得到分解因式的公式．例如图1，由一个边长为a的小正方形与两个长、宽分别为a、b的小矩形组成矩形ABCD，则整个图形可表达出一些有关分解因式的等式．

三、学会概括和提炼，制作自己的知识网络图

以章节为单位，根据课本上的相关线索或自己确定的线索，制作属于自己的知识网络图．这样，你就可以把单一的知识转化为你所用的知识工具了．

现在课本和教辅书上有许多知识网络图，那是别人智慧的结晶，是他人的知识产权．你看过后，印象不会太深．而你浏览课本后，尝试着按自己的思路、思维方式编写出来知识网络图，即使不全面，但对自己能力的提升会更有意义．

例如，在一元一次不等式中，我是按这样的线索把它们连接的．

第一线索 由实际背景建立不等式，从而探索了不等式的基本性质，明确了解不等式的方法和解集在数轴上的表示方法．

第二线索 不等式的特例（一元一次不等式，一元一次不等式组），掌握它们的解法、解集及解集在数轴上的表示方法．

第三线索 不等式和不等式组的实际应用（应详细）．

绘制出知识网络图．

同学们不妨尝试按自己的思路编制出分解因式和分式的网络图．

四、借助课本中的经典例题和习题这个平台，促使这些题目不断升华，不断精彩

现在，有些同学不喜欢在复习时看课本的例题和习题，认为太简单，都会做．还有些同学会认为，部分题只要老师指点一下，就会做了．其实，老师的指点就是直接或间接地告诉你了思维模式，若没有这个暗示，你自己将怎样寻找题目的切入点呢？这就需要有一个量变到质变的过程．同学们都听说过“一题三见面”吧．第一次见面，要求会做；第二次见面，要分析出此题与哪些知识有关，与哪类题相仿或由哪类题的数学模型演变或拓展而来的；第三次见面，则要求更高了，在此题基础上，你能根据它内在的知识结构，组织或改编出一道与此相关的题．

最后，别忘了在复习的过程中注意细节问题．数学使人精细．它是一门追求“完美”的科学．不能因为一个细节、一个符号或一个数字的错误，影响了你的成绩，那才是得不偿失呢！

“衣带渐宽终不悔，为伊消得人憔悴．”这是我们学习数学的一种境界．经过你执著的追求，最终你会到达“蓦然回首，那人却在灯火阑珊处”的更高境界！