基于Labview的PID算法在小型水下机器人中的应用

1 引 言

图形化编程语言Labview在各种测试系统和控制仪器领域中，已经得到很广泛的应用，推动仪器工业的飞速发展。Labview开发环境使用图形化编程语言G语言编写程序，产生的是框图式程序，直观形象，它通过交互式图形化仪器面板提供丰富的控件，在后面板的图形化编程中封装了丰富的算法，如提供的数理统计、信号处理、仿真、IVI仪器驱动、网络通信、数据库管理等模块，都为软件开发带来了极大的方便。同时，Labview还提供了强大的数据采集功能，例如DAQ采集卡可以高速、高精度地采集各种类型的模拟信号，并且还具备高精度的D/A输出功能，通过计算机可很方便和迅速地对下位机仪器进行快速和高精度的数据采集。Labview封装的PID工具包集成了全面的PID控制算法，可以适合各个领域的高精度控制。PID控制是工业控制中应用最广泛的控制策略，它算法简单、鲁棒性好、可靠性高，在很多高精度控制的领域下都能达到非常满意的效果。本文主要是应用Labview的PID工具包实现PID算法程序编程，对机器人的运动进行控制，主要的被控对象是航向角与深度。

2 控制系统的组成及其控制原理

2.1 小型水下机器人简介

本文中提到的水下机器人是一种比较简朴的机器人，属于ROV类型(带电缆)。主要用于在静水或缓流环境进行水中探测，包括船底探测、拍照、桥墩探测等。它具有体积小巧、控制灵敏、运动灵活等优点。在组成上主要有螺旋桨，提供机器人的运动动力，包括推进和方向控制；其他组成有图像扫描声呐、水深定位扫描声呐、CCD图像拍摄等。机器人的所有数据通过RS 232方式转换成CAN方式进行传输，再由CAN转换成RS 232进入计算机，从而可以方便地在计算机上对机器人进行控制。

2.2 PID控制原理

PID(Proportional Integral Derivative)控制是从比例、积分和微分三个环节实现对对象的控制，它的控制原理[1]如图1所示。

PID控制的典型特点是将给定值r(t)与输出c(t)进行比较得到系统偏差e(t)，从而进行比例P、积分I、微分D计算得到输出控制量u(t)，其控制规律具体可以由下面方程描述：

式中，Kp是系统增益系数；e(t)是给定与输出的偏差；Ti是积分时间；Td是微分时间。

PID的比例P部分按线性规律反映控制系统偏差的变化，因为，在系统工作时给定与输出的反馈是在不断地进行比较，一旦出现偏差，该环节可以快速响应，对系统控制量做出补偿，但会一直存在残差。所以在PID控制中，为了达到较好的效果需引入积分环节。该环节是属于无残差控制，可以消除系统残差，提高系统无差度，但是会造成系统响应过冲，Ti积分时间越大，过冲就越大；而微分环节的加入则可以减少由于积分控制所造成的响应振荡，Td越大，效果就越好。微分环节起到反映系统误差变化趋势的作用，也就是可以预示误差，在误差即将出现时，就使得积分环节中能超前起作用，这样就能有效地减少振荡[2]。

2.3 Labview中的PID工具包

Labview作为一种图形化的编程语言，可以非常方便用户对各种算法及其控制方案进行编程。美国NI公司最新推出的Labview8.2开发环境中，附带有丰富的PID子VI，例如：PID VI、PID Advanced VI等；同时还封装了对偏差输入的滤波功能VI，如PID Control Input Filter VI。用户不需自己通过Labview的框图程序具体编写PID算法的每一个细节，只要根据实际情况选择适合参数的子VI，把控制系统的反馈量和控制给定量两个关键参数连接到PID VI上，简单地配置好比例、积分、微分等参数，就可以对系统进行有效控制。

3 控制方案的实现

3．1 控制程序设计

小型水下机器人自身带有电子罗盘(指南针)和压力传感器，能够实时地反馈各自的数据。电子罗盘的数据为大地坐标中指南针的角度，用于指向当前机器人的运动方向，而压力传感器则是反映机器人在水中受到压力的大小，可以根据标定换算成其处于水中的深度。其控制原理[3]可以由图2表示。

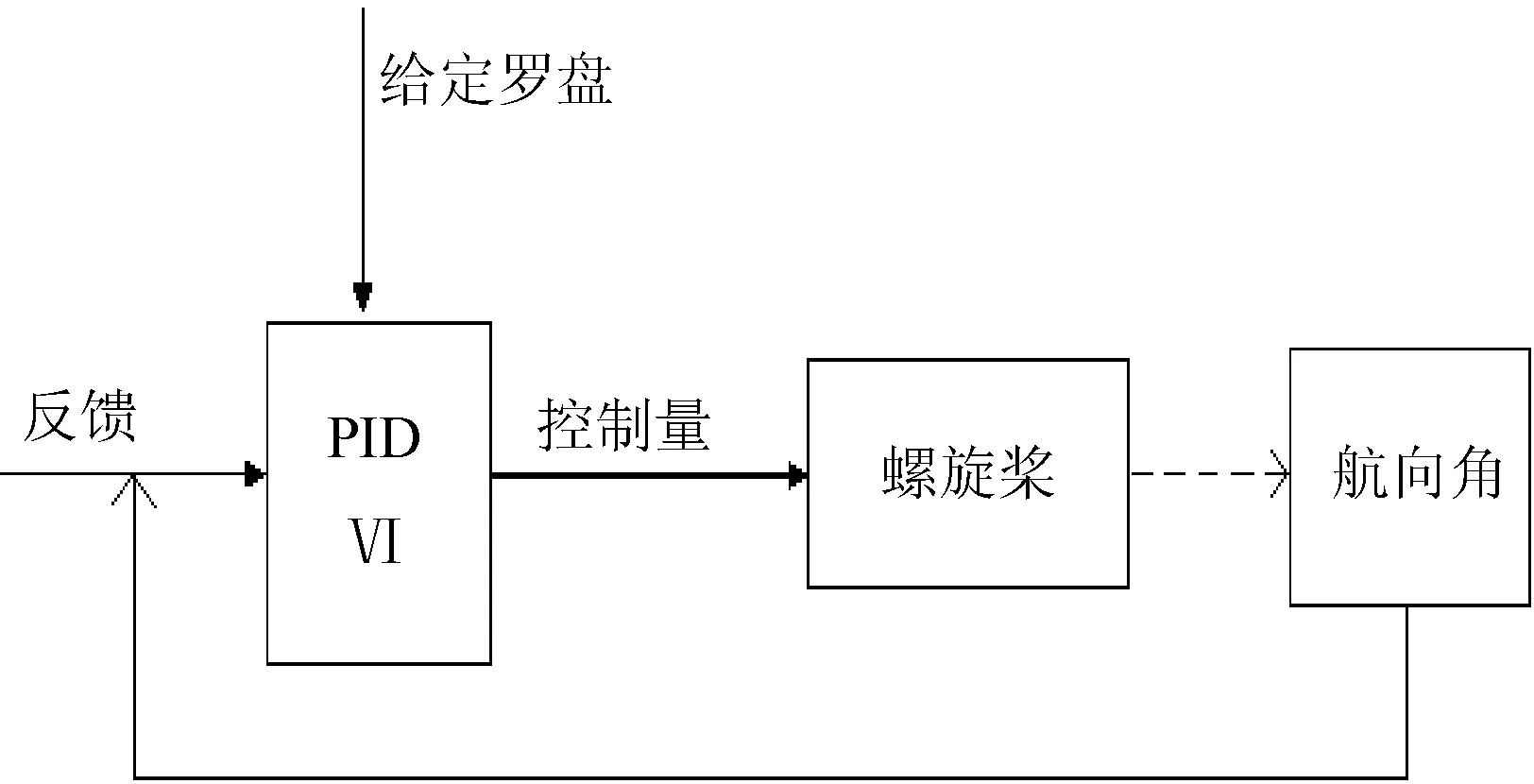
图2 螺旋桨PID控制

把机器人反馈的电子罗盘数据与控制用户给定的数据作为PID VI的输入参数，然后让PID VI进行PID的算法计算从而得到控制量，再以指令形式传输给机器人。机器人中的CPU电路再把控制量指令通过驱动电路驱动螺旋桨，从而完成一个闭环的控制系统。机器人的运动方向和潜水深度分别是由水平方向上两个螺旋桨的转向和垂直方向的螺旋桨进行控制。对深度控制量输出是把压力传感器反馈的数值按标定换算成深度(Depth)，然后作为PID VI的反馈量输入，经过PID算法进行比例、积分、微分计算后得到输出控制量。所以，在本文的控制方案中需要通过两路独立的Labview框图程序对机器人进行全方位控制。其面板控制设计及后台程序如图3、图4所示。

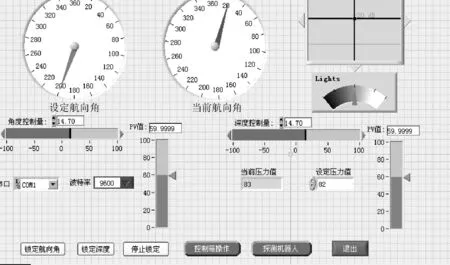
图3 面板控制设计

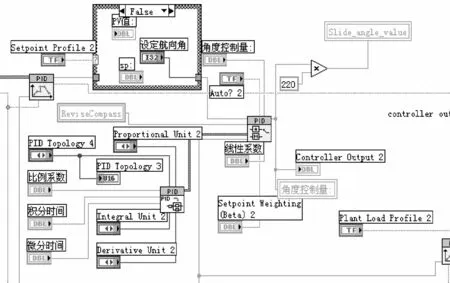
图4 后台Labview PID程序

本文中主要用到Labview8.2 PID工具包里面的convert PID parameters VI；PID Advanced VI和PID Setpoint Profile VI等。通过convert PID parameters VI把用户设定的PID控制参数包括系统增益、线性环节比例系数、积分时间、微分时间作为PID Advanced VI的PID gain参数输入，从而构成完整的PID程序[4，5]。

3.2 给定与反馈的电子罗盘校正

PID控制算法的控制量是一个直线型变化的输出，也就说通过PID计算后的控制量u(t)是一个一维方向上的数值，从负数到正数或者从正数到负数的来回变化，理论上可以向数轴两端无限变化，不出现周期性的规律，如图5所示。

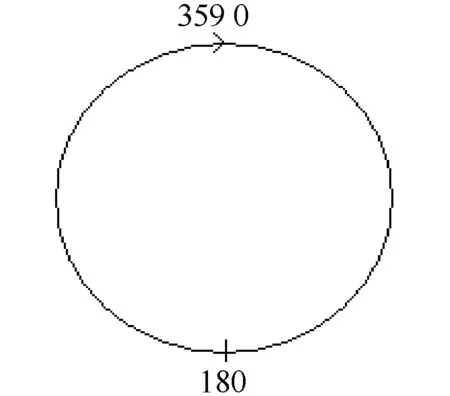
图6 航向角变化规律

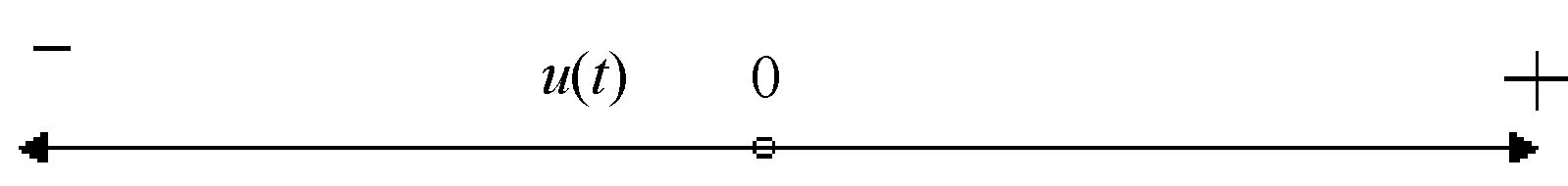
图5 PID输出常规变化规律

但机器人的航向角是周期性变化的，如图6所示，在0°～359°可以认为符合PID输出的常规变化规律。在这个范围内，如果给定的Compass-反馈的Compass> 0，则u(t)输出负数，偏差越大u(t)输出越大。如果给定Compass-反馈Compass< 0，则u(t)输出正值，偏差越大输出越大。如果仅在这个范围内Compass不做任何校正就可以得到有效的控制结果。但是，机器人的Compass除了在0°～359°内变化外，还存在从359°～0°或从0°～359°的跃变过程，称之为越零变化，这是因为航向角是周期性的。在这种情况下，如果Compass不做校正处理，直接作为PID的输入，就会得到严重错误的控制量，从而引起被控对象振荡。

为了解决上述航向角周期性变化引起的PID控制不稳定情况，本文需要先对反馈的Compass数值进行校正后再作为PID反馈参数输入。如果机器人在PID调整过程中从顺时针方向出现越零点跃变，那么，对反馈的Compass进行加360°处理，使得输入的反馈参数是大于360°的数值；如果机器人的Compass从逆时针方向越零跳变，那就对反馈的Compass进行减360°处理，使输入反馈参数是一个小于0的数值，这样从PID的角度看，航向角就不呈现周期性。

另一方面，在深度控制上因为深度Depth的数值是呈直线型变化，所以只需要直接作为反馈参数输入，就能使用PID控制算法。

4 实验测试

对Compass的控制中主要设定的参数包括给定值SetPoint、反馈值 Feedback Point、总增益 Proportional、线性环节系数比 Linearity等。当增大Proportional时(线性系数、积分时间、微分时间也随之增大)，机器人的响应速度随之增大，但是整个调整过程包括每次摆动范围也都明显增大，机器人最终稳定的时间也随之延长。如果单独调整参数Linearity时，则每次改变SetPoint时，最初会有比较大的过冲，造成机器人比较大的摆动。但由于PID积分环节的作用，所以经过几次比较剧烈的摆动后，机器人会很快地稳定下来。通过调整各个PID参数，可以很直观观察到各个参数对控制效果的影响。图8所示是在一个约0.6 m/s人工水流的水池里完成试验的试验结果，曲线反映了航向角在某一次调整时的变化过程，是控制机器人从153°调整到180°的过程。在本次试验中，设定的参数有Proportion=5,linearity=3,integral=0.05,derivative=0.04。

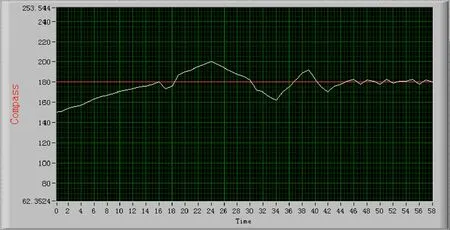
图8 航向角向180°调整过程

5 结束语

利用Labview进行控制软件开发具有很大的灵活性，并且易学易懂，其软件界面形象生动。无论是控制领域软件开发，或者计算机网络软件，甚至数字信号处理上都极具方便，特别是PID工具包的应用，大大缩短了整个控制系统的开发周期。本文通过其PID工具包，尤其是Labview新版中集成的PID子VI的应用，大大简化了编程的复杂度。总之，利用Labview进行编程可以非常有效地避免了通过文本语言编写程序和调试系统的繁琐过程。

[1] 金志强，包启亮.一种基于LABVIEW的PID控制器设计的方法[J]．微计算机信息,2005(6S)：1-2,71.

[2] 陈积文.一种基于Labview图形化编程的PID控制算法及其应用[J].自动化技术与应用，2007(5)：42-45.

[3] 朱利辉，邹轩，徐新华.基于Labview的直流电机速度控制系统[J].仪器登记表用户，2006(1)：14-15.

[4] 陈东,姚成法.基于LABVIEW步进电机PID控制系统的设计[J]．工业仪表与自动化装置,2005(1):48-49.

[5] 唐进元,黄云飞.基于LABVIEW的数字PID控制器的设计研究[J]．测控技术,2000(4):35-37.