机械设备对基座激励力估算方法研究

1 引 言

结构动力学有三类基本问题[1]：在已知激励、响应、系统动力特性(包括振源的弹性系统和输出对象结构系统的各种参数)三者之二的情况下求取第三个量。如果已知激励和响应欲求其系统特性称为第一类逆问题，根据响应和系统特性求激励称为第二类逆问题。在许多工程实际问题中，均假设激励力为单位激励，通过计算得到系统的振动响应数据来分析系统的振动特性，这种分析方法在一定程度上可以为实际问题提供指导。然而单位力载荷显然不能体现各频率点之间的量级关系和差别，带入实际问题分析有些欠妥，例如隔振问题中对系统实际隔振效果的分析就与激励频谱有关。当然，最可靠和最为理想的激励谱估计应该通过实测途径才能获得，通过在机械设备机脚安装力传感器可以直接测量设备的输出激励谱，但测力传感器的安装与拆卸往往非常困难，可行性较差。在输出激励力频谱不方便直接测量的情况下，考虑通过间接估计方法对设备实际激励力频谱进行估算[2,3]，有一定的工程应用价值。

2 基本理论

2.1 有限元法基本理论

有限元法的基本思路是“一分一合”，分是为了进行单元分析，合是为了对整体进行综合分析。其基本原理是：在变分法或加权余量法的基础上，采用分块逼近的思想而形成的系统化的数值方法。其基本原理是将求解区域进行离散化，剖分成相互连接而又不重叠的一定形状的子区域，称为“单元”。在单元中选择基函数，用单元基函数的线性组合来逼近单元中的真解。总体基函数可以看作由单元基函数所组成。同时总体区域上的积分也可由各个单元的积分之和来合成，由于单元的几何形状是规则的，因此在单元上构造基函数可以给出一定的法则，单元积分也比较容易。有限元法中的总体区域的解可以看作是由所有单元上的近似解构成。

通过对结构进行单元离散，结构方程可以写成下列形式：

(1)

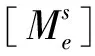
2.2 导纳分析法基本理论

对于稳定的、定常的、线性振动系统在简谐力f=Fejωt作用下，其相应的稳态运动响应在复平面中为x=Xej(ωt+φ)，则该系统的机械导纳可以表示为：

(2)

由于激励与响应的幅值比及相位差均随激振频率ω而改变，而机械导纳则是以jω为参量的复变函数，故它们都是频域函数，则上式可以进一步表示为：

(3)

对于m个输入和n个输出的线性振动系统，可用广义导纳矩阵或传递函数矩阵来综合描述它在频域内的动态特性[4]。

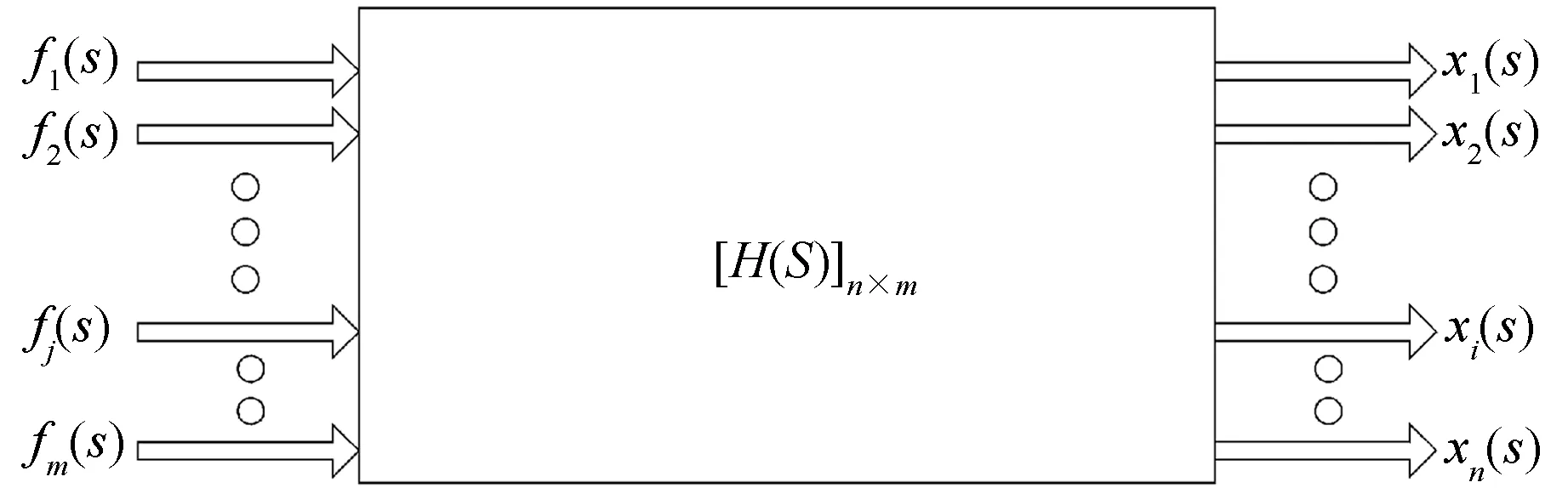
图1 多输入输出线性振动系统

其中：

(4)

式中，hij(s)代表第j个输入与第i个输出之间的权函数。

3 弹性壳体模型算例分析

3.1 壳体模型结构的基本参数

弹性壳体的主体结构由截顶圆锥壳(长0.85 m，两底面直径分别为0.1 m和0.9 m)、圆柱壳(长3.025 m，直径0.9 m)和椭球冠封头(高0.225 m，球冠直径0.9 m)三部分拼接而成，内部还有机械设备安装基座、舱壁、舱底纵骨和环肋等部分。

3.2 估算方法流程

首先采用ANSYS有限元软件，建立此弹性壳体的有限元数值计算模型。表面壳体、设备基座以及舱壁结构用shell63单元模拟，单元的总数为39 490个；环肋结构用beam188单元模拟，单元数为4 929个。在30～300 Hz频率范围内，每隔10 Hz取一个分析频率点，仅考虑机械设备为刚性安装条件，在设备对基座激励的4个机脚上加载垂向单位力，进行谐响应分析计算，得到设备机脚激励点的响应加速度值，可组成一个4×4阶的加速度矩阵，由导纳法的基本原理可知，该矩阵也即4个机脚激励点之间的导纳复矩阵：

(m,n=1,2,3,4)

(5)

式中，amn(ωi)为在第m点作用垂向单位力时第n点的加速度响应值，ωi为计算频率值。

在弹性壳体模型试验中，使用了Sony磁带记录仪以及LMS公司的pimento测试与分析系统，对模型进行了悬空吊装振动响应测试，同步测量了机械设备斜对角2个机脚处的垂向加速度和壳体内表面测点处的垂向加速度。由于壳体为对称结构，对称位置处的机脚用相同的加速度试验数据，合并写成机脚的实测加速度矩阵：

[Acc(ωi)]=

[Acc1(ωi)Acc2(ωi)Acc3(ωi)Acc4(ωi)]T

(6)

式中，Accm(ωi)(m=1,2,3,4)为第m个机脚处在模型试验中测量得到的加速度响应值；ωi为计算频率值。

结合数值计算得到的导纳传递矩阵[A(ωi)]和机脚加速度试验数据[Acc(ωi)]，根据导纳法的基本原理得到下式：

[Acc(ωi)]=[A(ωi)][F(ωi)]

(7)

可求得在某一频率下的机械设备对基座输出激励力：

[F(ωi)]=[F1(ωi)F2(ωi)F3(ωi)F4(ωi) ]T

=[A(ωi)]+[Acc(ωi)]

(8)

式中[A(ωi)]+为[A(ωi)]的Moore-Penrose广义逆。

以此类推，就可以求得设备对基座的输出激励谱[F]。

将输出激励谱[F]带入弹性壳体有限元模型，计算得到壳体表面测点处的加速度值。并将壳体表面测点处加速度响应的数值计算结果和试验测量结果进行对比分析，给出了壳体表面4个测点处的加速度计算值和试验值的对比图谱，见图2。

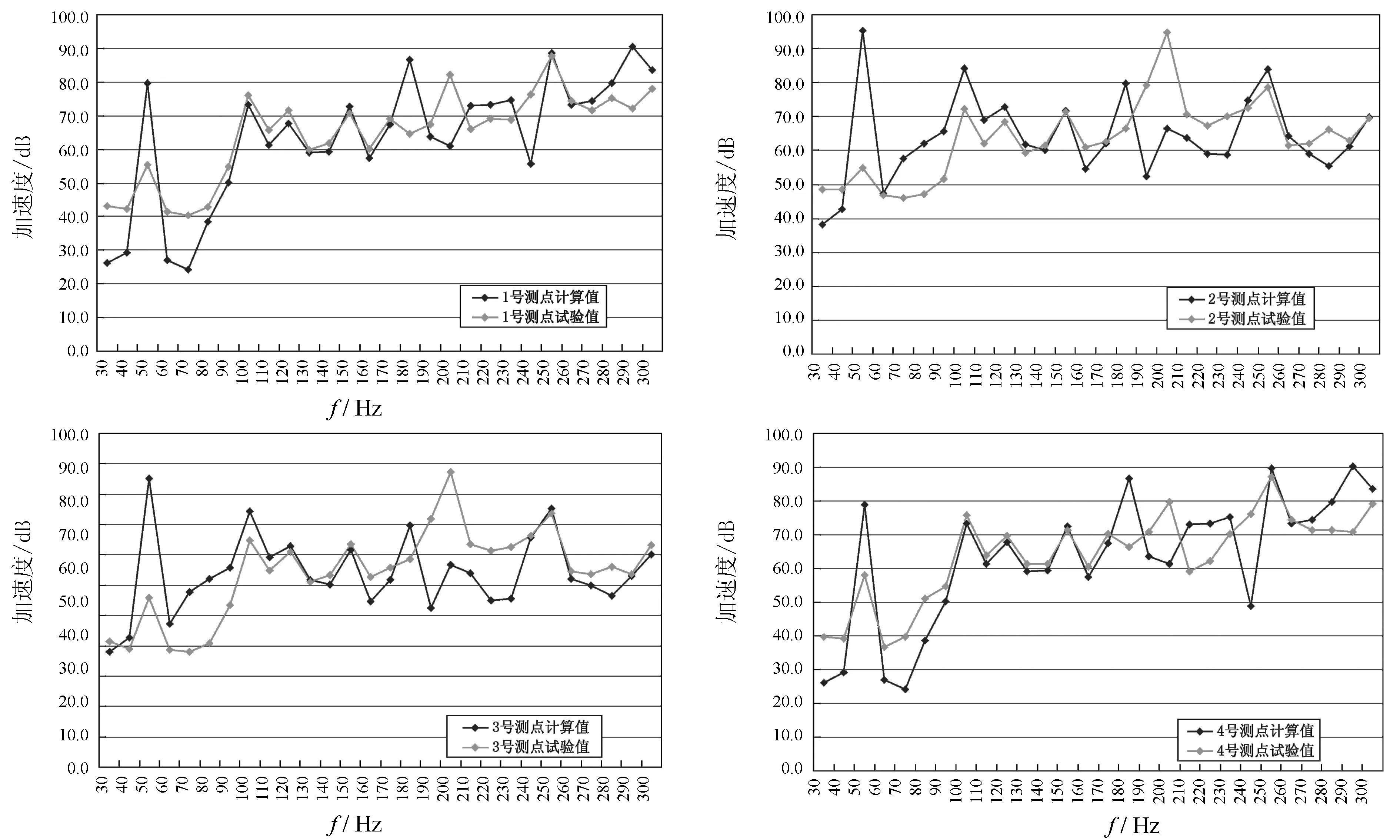
图2 弹性壳体内表面测点加速度计算值和试验值对比

由图2看出，在30～300 Hz频率范围内，壳体内表面测点加速度计算值和试验值趋势大体一致；但在某些频率点处数值上相差比较大，主要是因为在理论计算和实际试验中做了一定程度的简化，例如：机械设备的输出激励力仅考虑了垂向的影响而忽略了水平方向的影响；机械设备和基座由螺栓连接，在实际情况中并不是完全刚性的，而且在接触面积上实际应为面接触，而理论分析中都视为点接触；对称位置的机脚测点采用相同的加速度试验值带入求解，而实际上对称测点处加速度值是有差别的。同样，在分析时将机脚测点的位置等同认为就是机械设备对基座的输出激励力位置，而实际上两者之间还有一定的距离。上述这些都会对数值计算结果产生影响。图2中某些频率处的计算和试验的加速度曲线走势有反相突变，是因为有限元计算推导得到的导纳复矩阵中包含机脚激励点之间的相位信息而试验数据中没有彼此的相位信息，将各点简化处理成同相位考虑了。

4 结 论

本文运用有限元法间接求得了机械设备对基座激励点处的广义导纳矩阵，在一定程度上避开了通过实测途径求该导纳矩阵的困难，而且结合机械设备机脚加速度实测数据，间接估算了机械设备对基座的激励力，并通过带入估算得到的激励力求壳体结构表面的响应和实验测量的响应数据进行对比，结果表明该方法可行，具有一定的工程应用价值；同时为了提高该方法计算精度，在有限元建模方面需要进一步的细化，考虑机械设备对基座在水平方向激励的影响，改进试验数据的后处理过程，能在试验数据中提取出激励力作用点之间的相位信息，这都要求在今后的理论和试验中不断完善，不断改进。

[1] 朱石坚，何琳．船舶振动控制机械[M]．北京：国防工业出版社，2006.

[2] 翁雪涛，王家林，朱石坚．利用频率响应函数求外部激励[J]．噪声与振动控制，1999(1)：12-14.

[3] 翁雪涛，朱石坚．利用频率响应函数求外部激励的实验验证[J]．噪声与振动控制，1999(3)：9-11.

[4] 左鹤声．机械阻抗方法与应用[M]．北京：机械工业出版社，1987.