基于FLUENT的90°圆形弯管内部流场分析

1 引 言

弯管在工业、农业以及造船业使用非常广泛，例如：舰船上受到空间布置的限制，弯管被广泛使用在主疏水系统管路、海水冷却管路以及滑油管路等管路系统中，这些功能各异的弯管实现了流体输送和热量、质量交换等功能。由于受到众多因素的影响，诸如弯管的弯曲程度、流体的流动马赫数(Mach)、 流体运动方向等，弯管内的流场呈现出十分复杂的流动特性。例如：在管壁附近形成分离区,管道横截面上产生二次流动,这些现象不仅造成流体总压和能量的损失,而且形成的局部障碍区域也使流动系统的阻力增大,降低了热量、质量的交换效率。因此,弯管内的流动一直受到内流研究者的关注[ 1-3 ]。

在早期的研究中，主要采用实验测量的方法，例如文献[1]采用的是旋转探针技术对Rc/D=2的90°圆截面弯管内的紊流场进行了实验研究，并给出了若干个轴向截面的速度等值图、矢量图以及雷诺应力等值图等。文献[2]采用激光多谱勒测速仪对90°方形截面弯管内流进行了系统的研究,给出了层流和湍流两种流态下的时均速度分布,以及弯曲段壁面的压力分布等实验结果。文献[3]用CTA热线风速仪和五孔探针，对一曲率直径比Rc/D=0.87、直径D=280 mm的圆截面弯管内部三维紊流流场进行了详细测量和分析。给出了不同雷诺数下弯管内不同截面上时均速度场、紊流动能、总压及静压沿曲率半径方向的分布。

在理论计算方面，文献[4]和[5]分别采用大涡模拟和双层k-ε 湍流模型对弯管的内部流场进行了数值模拟，都取得了较好的模拟结果。但是，他们主要是对方形截面的弯管进行数值模拟，对圆形截面的弯管内流场进行数值模拟的文献较少，而且这些文献只对弯管内流场的流动特性进行分析，却没有对各截面二次流的产生原因和情况进行分析，因此对工程贡献不是很大。本文针对这种情况，使用CFD商业软件FLUENT对弯管内部流场进行模拟，选用RNGk-ε湍流模型，并将计算结果与文献[1]的实验结果进行对比，判断数值模拟的可靠性。

2 控制方程和数值模拟

2.1 控制方程和RNG k-ε湍流模型

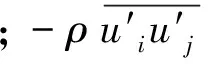
RNGk-ε湍流模型的湍动能传输方程为:

Gk-ρε

式中，αk、αε分别表示κ方程和ε方程的湍流Prandtl数；Gk代表由平均速度梯度引起的湍动能生成项。在ε方程中，Rε为ε方程中的附加源项，代表平均应变率对ε的影响，Rε的表达式为：

上述方程的模型参数为：η0=4.38,β=0.012,Cu=0.084 5,C1ε=1.42,C2ε=1.68,αk=αε=0.719 4。其中η是无量纲应变,或者湍流时间与应变尺度的比值，代表平均应变率对ε的影响。

RNGk-ε湍流模型既适应高雷诺数情况，也适应低雷诺数下的湍流流动，即提供了一个微分形式的有效粘性系数表达式，以说明低雷诺数流动效应。此外，对于湍流Prandtl数，RNGk-ε湍流模式提供了一个解析式，而标准k-ε湍流模式使用了经验常数。

2.2 几何结构和网格的生成

本算例的研究对象为90°圆截面弯管，其几何尺寸如图1所示。为了分析方便，将弯管分成上游直线段、弯曲段和下游直线段3部分。弯管的曲率直径比为Rc/D=2，弯管直径D为104 mm，上、下游的直线段长度均为1 040 mm，φ为极角，并定义弯曲段的主流入口截面处φ= 0°，弯曲段出口截面处φ= 90°，曲率半径Rc=208 mm,坐标系原点O位于弯管曲率半径的中心。其中U′和U表示沿弯管中轴线的纵向距离。

图1 弯管二维结构示意图

本文使用FLUENT软件中的前处理程序gambit生成计算区域几何体，再进行网格划分，得到如图2所示的六面体结构网格单元。

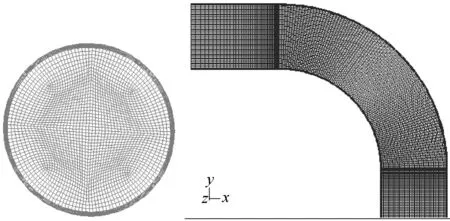
图2 弯管横剖面和纵剖面网格图

2.3 边界条件

边界的进口条件：均匀来流速度大小为8.7 m/s，方向垂直于弯管的入口截面即y-z平面，温度300 K。边界的出口条件：出口压力0 Pa。壁面条件:固体壁面上采用无滑移条件。

3 计算结果与分析

3.1 横截面速度等值线图和矢量图

如图3所示，在U′/d=-1时，由于流体还未受到弯曲段的影响，该截面的速度等值图是同心圆。当φ= 0°时，由于内壁附近轴向压力值减小(图6)，在内壁面附近的流体速度略有增加。同时，外壁面在压力值增加的条件下,外壁面附近的流体速度开始减小。当φ= 30°时，速度较高的流体向弯曲段的内壁面流动，由于离心力的作用二次流在横剖面内产生，并且弯管中心的流体向外扩散，上部和下部附近的流体向内扩散,如图4(a)所示。当φ= 60°时，二次流带动内壁面附近的高速流体穿过横截面的中心区域向外壁面流动，与此相应，上部和下部壁面附近的低速流体在二次流的作用下,沿着壁面向内壁面流动,如图4(b)所示。因此，此处的内壁面附近的轴向压力增加，而流体速度开始减小，接着由于强二次流的作用主流中的高速流体继续沿着弯管的对称横剖面向外壁面流动。从φ= 75°到φ= 90°，沿着壁面向内壁面流动的二次流,带动向外壁面流动的高速流体向内壁面流动，从而致使速度等值图扭曲变形，其速度等值图呈舌状并且包围了在内壁附近的低速流体。在U/d=0.5和U/d=1之间，由于外部二次流的作用，内壁面附近的低速流体继续向弯管中心区域流动，并且在内壁面和弯管中心之间形成低压区(图5)。从U/d=2到U/d=5时，二次流逐渐减弱，其中心向管道的中心区移动，到达U/d=10时，由漩涡形成的二次流消失，轴向速度显示为同心圆轮廓。

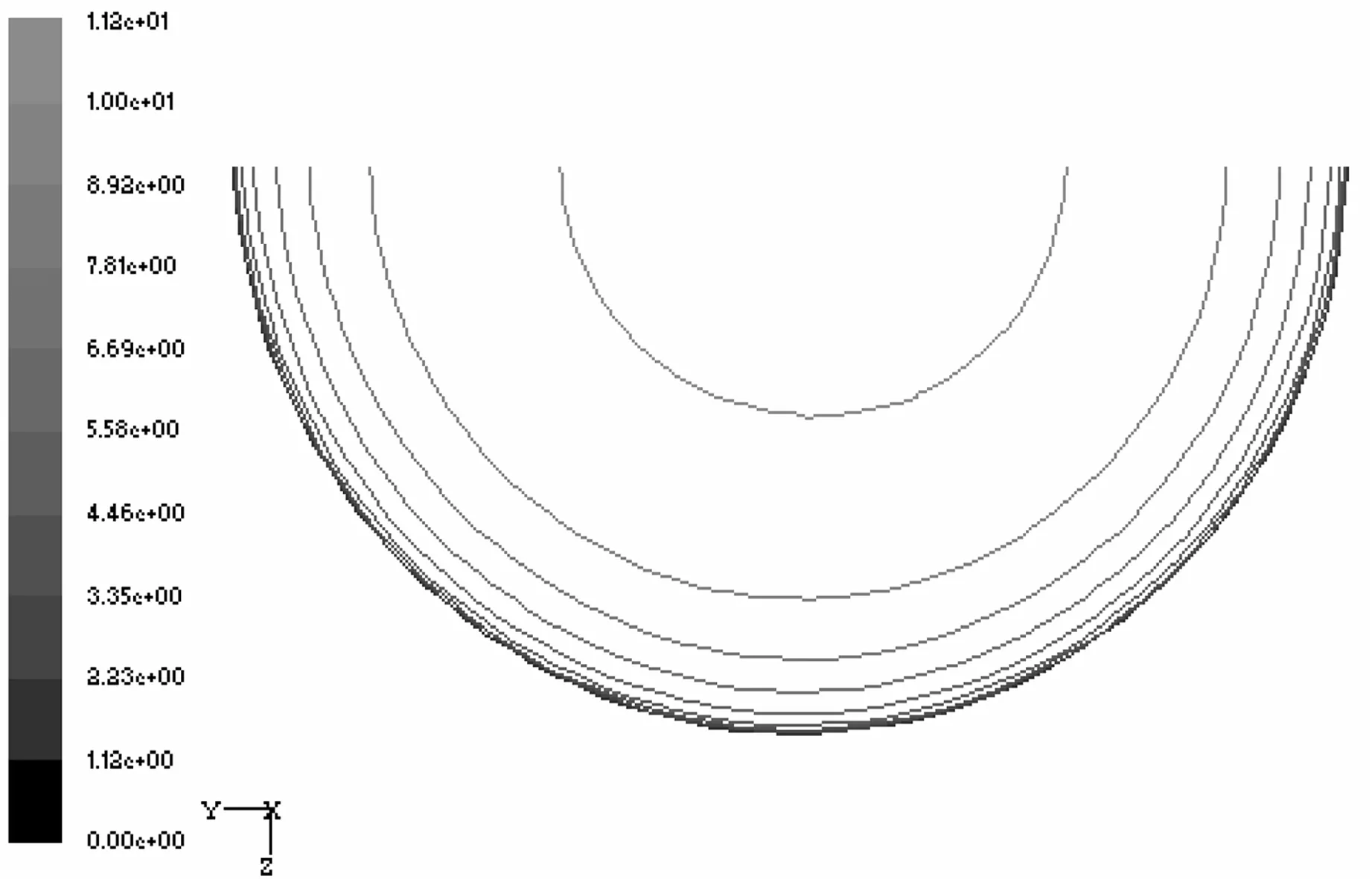
(a) U′/d=-1

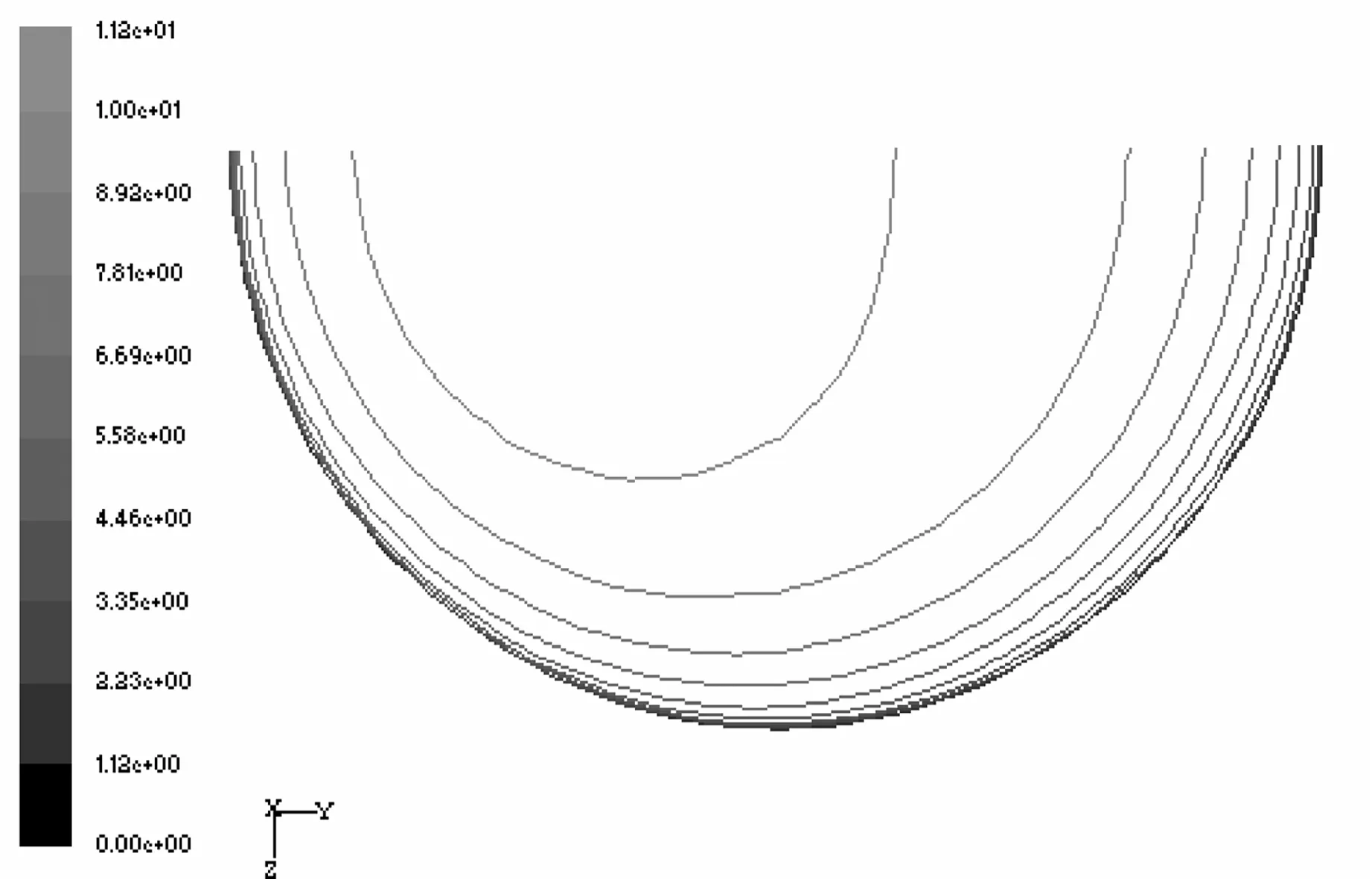
(b) φ= 0°

(c)φ= 30°

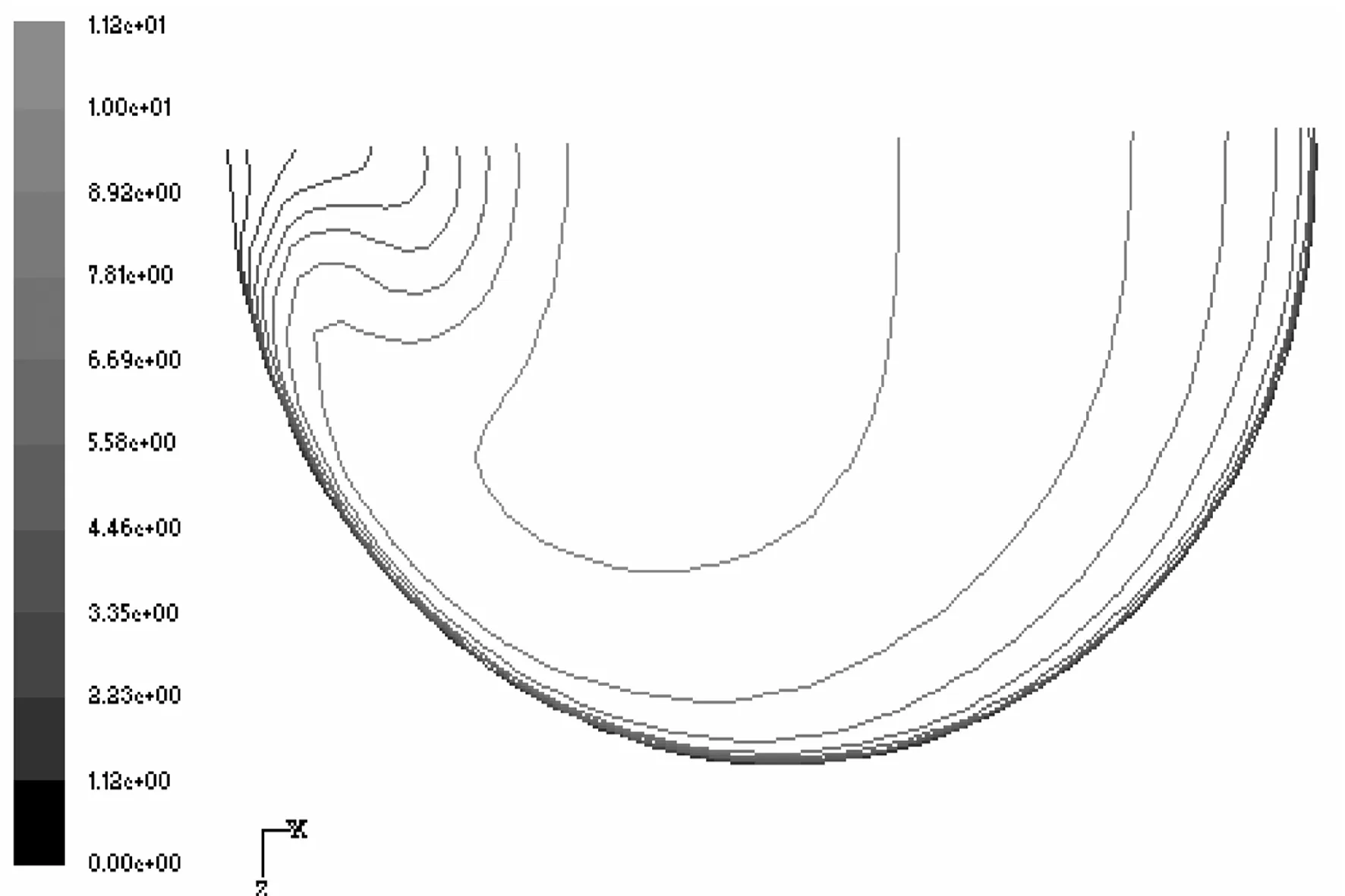
(d) φ= 60°

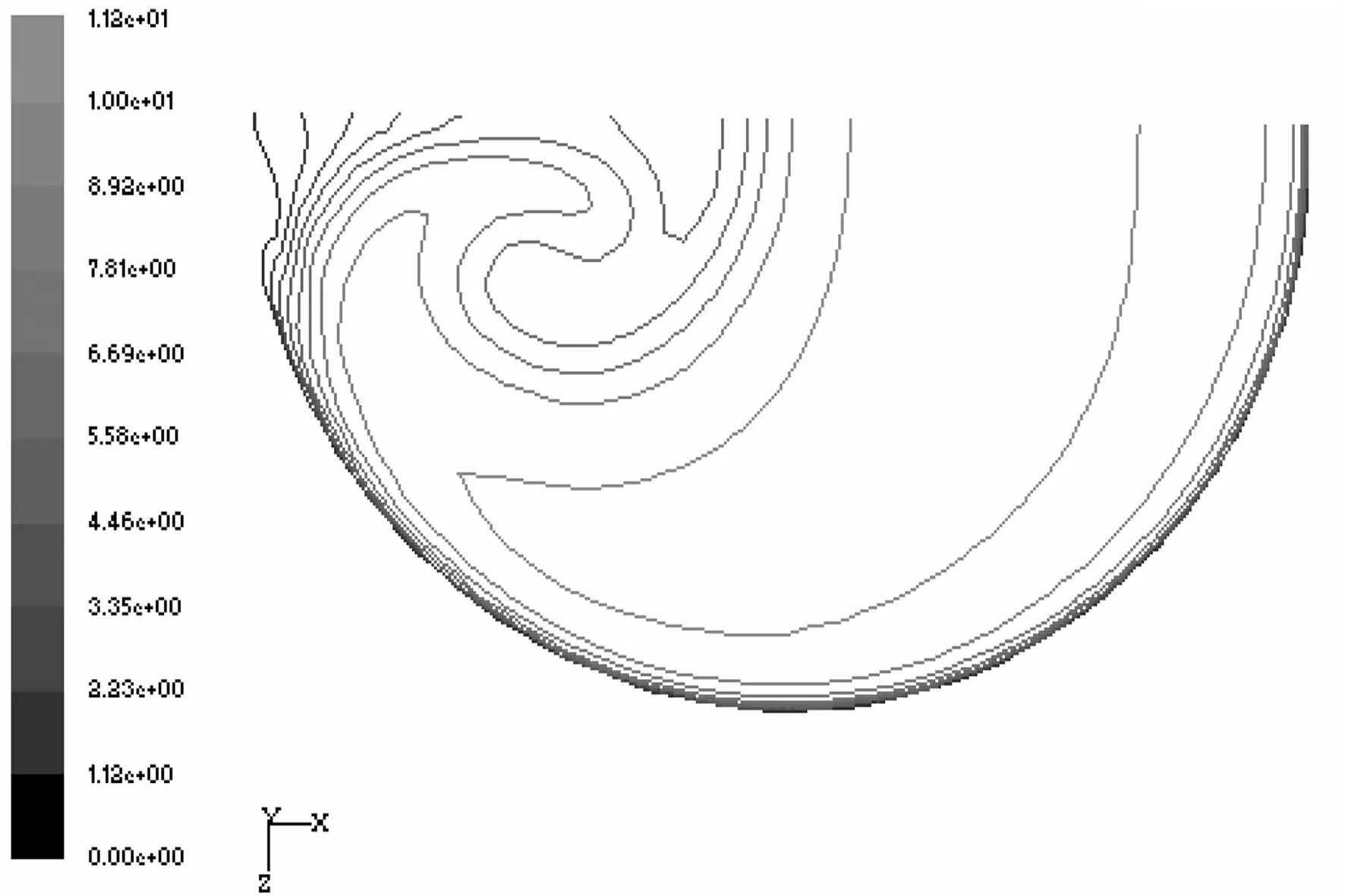
(e) φ= 90°

(f) U/d=1

(g) U/d=2

(h) U/d=5

(i) U/d=10

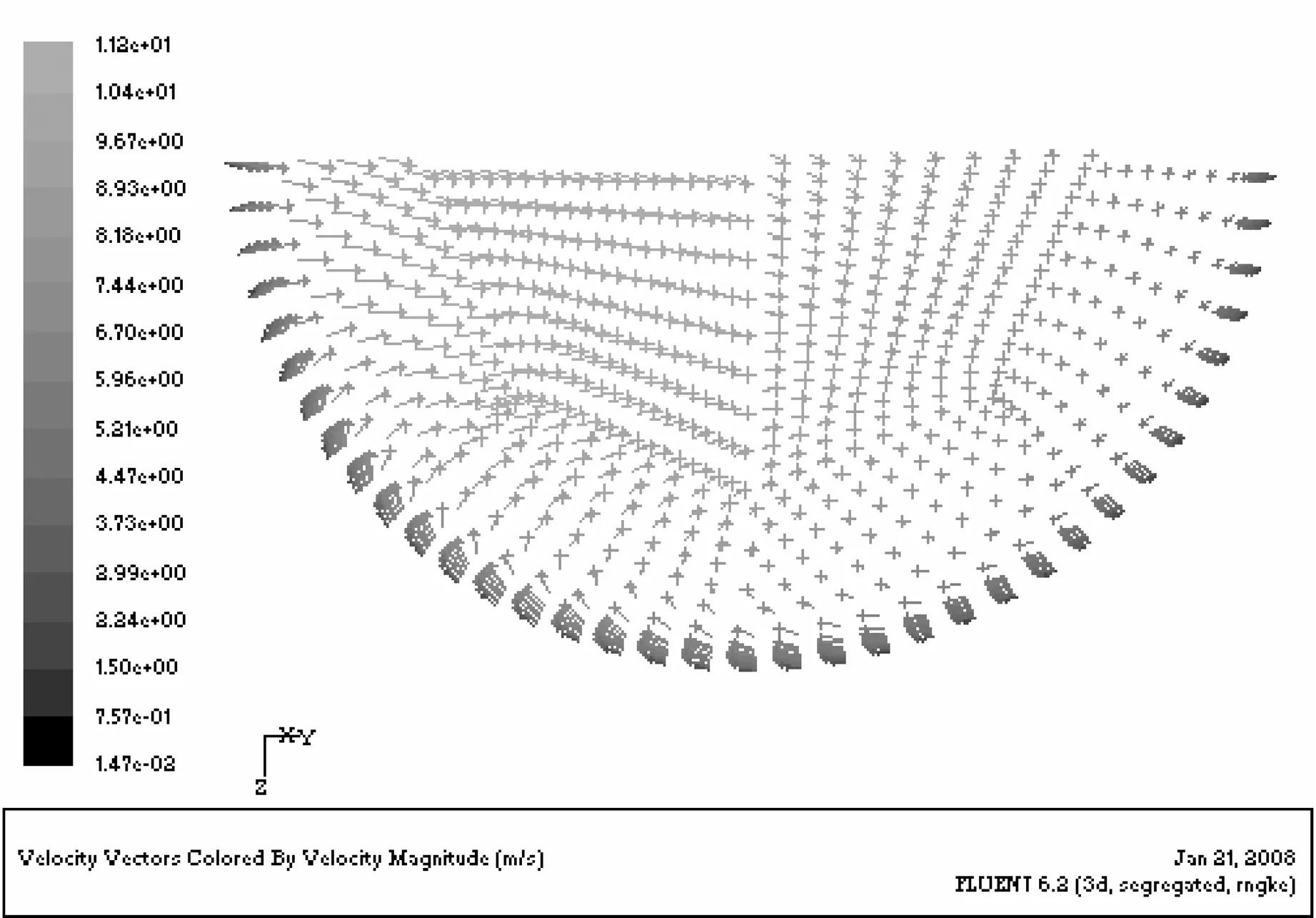
(a) φ=30°

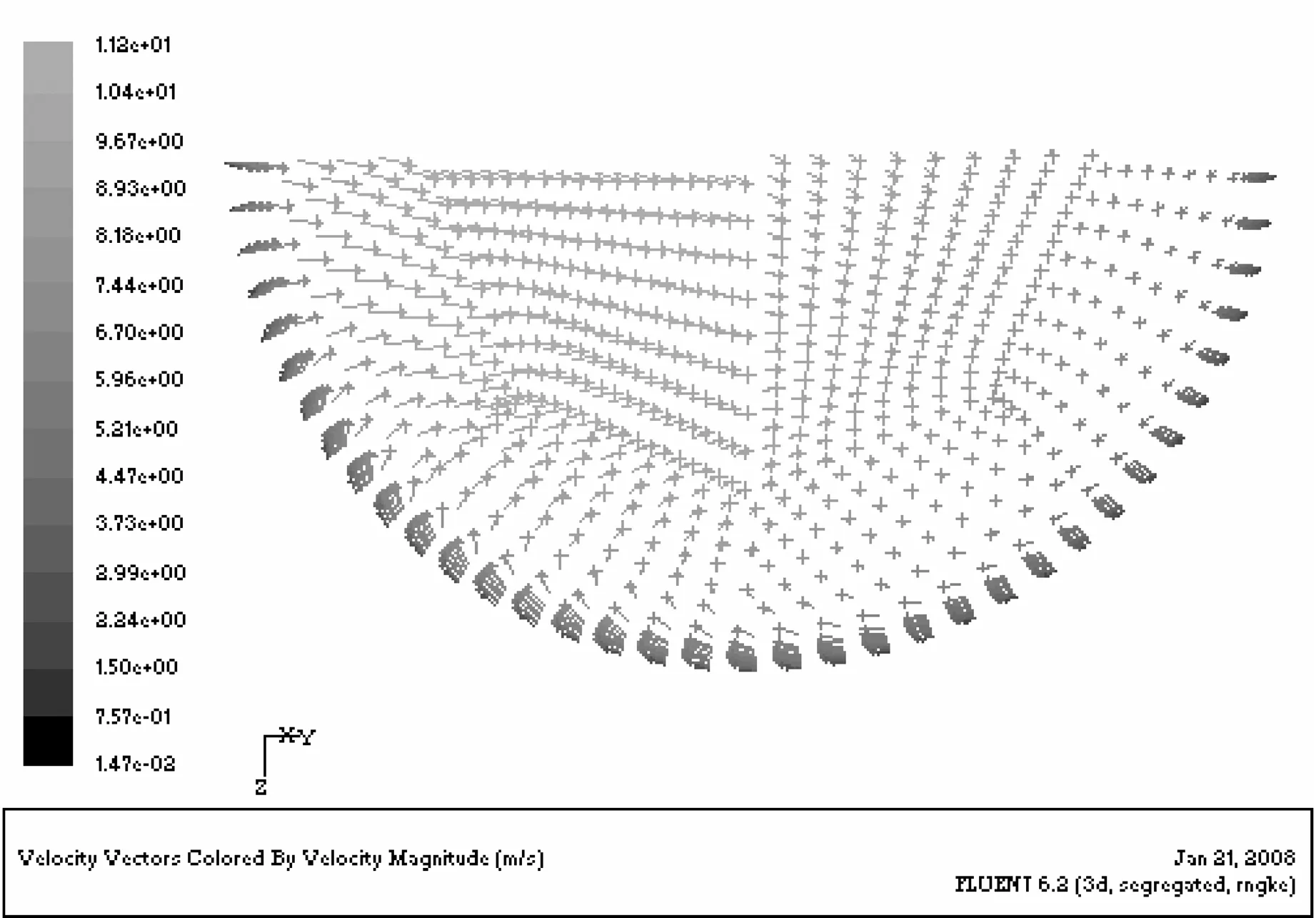
(b) φ= 60°

(c) φ=90°

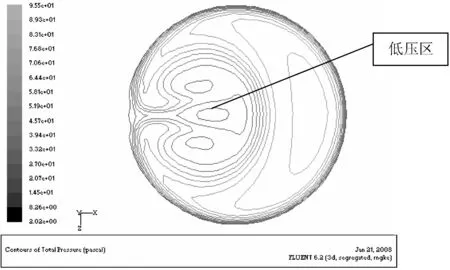
图5 U/d=1时的压力等值线图

3.2 压力分布曲线

图6展示了从弯管弯曲段前U′/d=-1处至弯曲段面后U/d=5处沿轴向方向的压力分布曲线。为了方便比较，这里将参考压力系数取为入口处的压力系数。图中可以清晰看到，在管道弯曲段内，沿轴向的压力梯度很大，且呈现出靠近内侧壁面区域的压力值小，外侧壁面附近区域压力值较大的分布情况。分析其原因，主要是流体在运动过程中受到弯管曲率的影响，因离心作用逐渐被甩到曲率半径较大的外侧壁面附近，导致众多流体推挤外侧壁面所致。此外，由于能量的损失造成弯管下游直线段处的压力值均小于上游直线段处的压力值。从图中可以看到，计算结果与实验结果吻合较好。

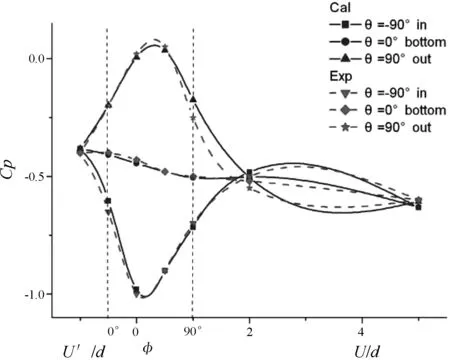
图6 弯管轴向压力分布曲线

3.3 纵剖面压力分布图和速度矢量图

从图7中的压力分布中可以看到，在弯管的弯曲段的外壁面附近压力较大，内壁面压力较小；相反，从图8中的速度矢量可以看到，在同样位置上，内壁面附近的速度较大，外壁面的速度较小，内壁面速度在弯曲段入口处开始增加，从极角φ= 60°时开始高速流体向外壁面流动，在弯曲段下游直管段，高速流体出现在直管的外壁面，且高速流体区域慢慢减小。从图上我们也可以看到，当φ= 90°时，即弯曲段出口附近出现低速区，存在较大涡流，这些与实验结果一致。

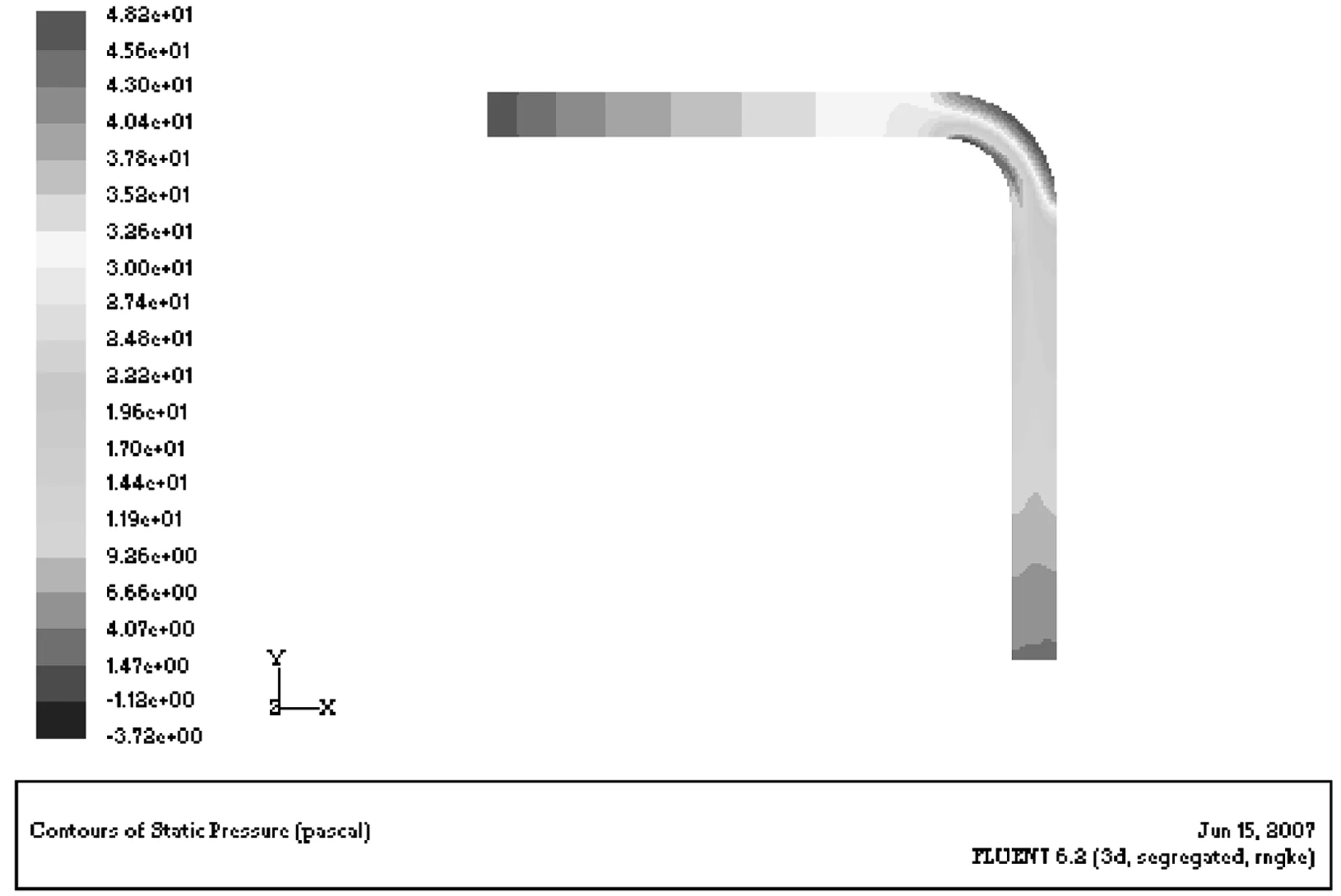
图7 纵剖面压力分布

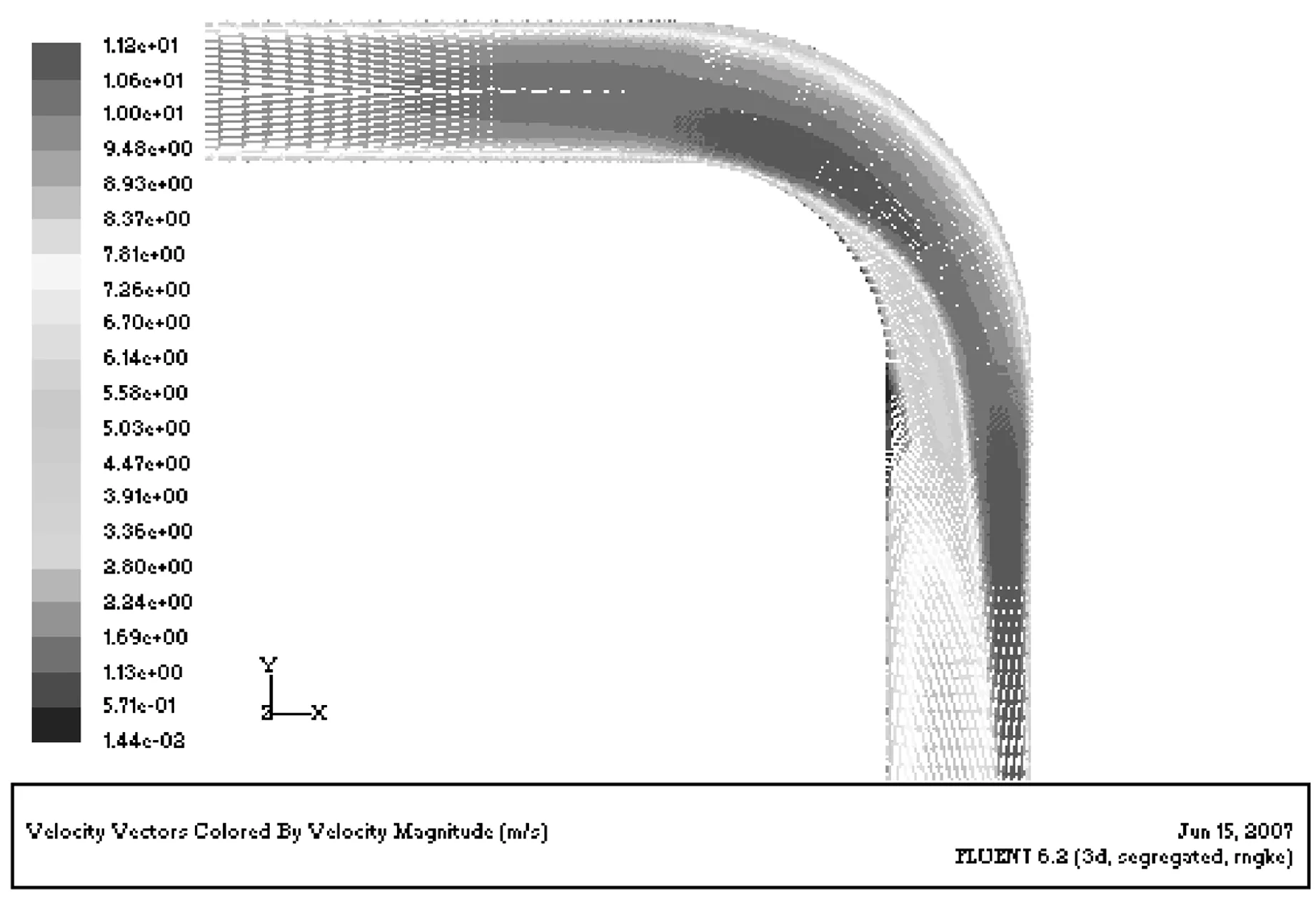
图8 纵剖面速度矢量图

4 结 论

1) 在弯管弯曲段入口，弯管内壁附近的主流速度开始增加，二次流从外壁面向内壁面移动。由于二次流的存在，整个弯曲段呈现外壁面压力大速度小，而内壁面呈现压力小速度大的现象。

2) 弯管存在着能量损失，造成弯管下游直线段的压力值比上游直线段的压力值小。

3) 采用FLUENT中的RNGk-ε湍流模型进行计算，数值计算结果与实验结果符合较好，表明RNGk-ε湍流模型对具有二次流的湍流流动具有较好的模拟，能准确反映弯管内部流态，对工程研究有很好的指导作用。

[1] SUDO K,SUNIDA M,HIBARA H. Experimental investigation on turbulent flow in a circular-sectioned 90-degree bend [J].Experiments in Fluids, 1998(25): 42-49.

[2] TAYLOR AMKP, WHITELAW J H, YIANNESKIS M. Curved ducts with strong secondary motion : velocity measurements of developing laminar and turbulent flow [J].Journal of Fluids Engineering,1982(104): 350-359.

[3] 尚虹,王尚锦,席光,袁民建.90°圆截面弯管内三维紊流场实验研究[J].航空动力学报,1994,9(3):263-266.

[4] 樊洪明,何钟怡,王小华.弯曲管段内流动的大涡模拟[J].水动力学研究与进展,2001,16A(1):78-83.

[5] 梁德旺,王国庆,吕兵.低速高湍流度90°弯管流动数值模拟[J]. 南京航空航天大学学报,2000,32(4):381-387.