基于图论的舰船通道路线优化

1 引 言

舰船通道设计是舰船总布置设计的重要任务之一，通道设计的优劣直接影响到总布置设计的合理性。广义的通道布置设计包括对走道、门、舱口、梯的布置等。一般的具体要求包括应便于战斗行动、人员流通、物品运送和设备搬运等各种活动的进行；流通路线应尽量短、直而流畅，并保证所有舱室和部位都可以到达等，这就涉及到线路的优化选择的问题。优化的通道布置和路线设计不仅可以提高船舶人流、物流的效率，而且非常有助于对舰船上管网电网布置、逃生消防等诸多方面的设计。

在通道路线优化设计这一问题上，一项重要的任务就是寻找两点之间的最短路径的问题，而最短路径的问题是图论理论的一个经典问题。从图论网络模型的角度看，寻找最短路径就是在指定网络中两结点间找一条阻碍强度最小的路径。根据阻碍强度的不同定义，最短路径不仅仅指一般地理意义上的距离最短，还可以引申到其它的度量，如时间、费用、线路容量等[1]。本文所研究的最短路径就是指行程时间最短的路径。

最短路径算法的选择与实现是通道路线设计的基础，最短路径算法是计算机科学与地理信息科学等领域的研究热点，很多网络相关问题均可纳入最短路径问题的范畴之中。经典的图论与不断发展完善的计算机数据结构及算法的有效结合使得新的最短路径算法不断涌现。作为舰船通道路线优化设计的一种尝试，本文利用图论的经典理论和人群流量理论研究舰船人员通道路线的优化设计及最优线路选择。首先介绍图论相关理论，对船舶通道进行路网抽象，建立网络图，然后根据人群流动的相关理论，选取不同拥挤情况下的人员移动速度，从而确定各条路段(包括楼梯)的行程时间。以行程时间作为通道网络的路权，得出路阻矩阵以选择一对起点/终点的最短时间路线为目标，建立最短路径问题的数学模型，利用经典的Floyd算法确定最短路径。将此方法应用于某舰艇多层甲板的通道网络中，计算结果并进行讨论，最后在此研究的基础上对通道设计相关问题的深化和拓展进行了探讨和总结，并提出设想。

2 最短路径问题的图论描述

2.1 图论及其相关概念

图论中的图的概念与通常意义上的图的概念是完全不同的，图论中的图是表明一些点及这些点之间的路线沟通情况，用点表示研究的对象，用边表示这些对象之间的联系。图论中将有序三元(或多元)组称为一幅图，即

G=(V，E，W)

式中，V为图中所有顶点(Node)的集合，V={v1,v2…，vn}；E为边(Edge)的集合，E={(e1，e2…，en)}；W(Weight)为各路段的道路权值。如果给图中的点和边赋予具体的含义和权值，并规定了起点和终点，这样的图即称为网络图。如果每条边上有箭头标注，称为有向图，如果将有向图去掉箭头，得到一个无向图，称为基础图。

2.2 路网结构的建立分析

路线优化技术通常采用图论中的“图”来表示路网，船舶通道路网与图论的路网对应关系为：

结点——通道的交叉口或断头路的终点；边——两结点之间的路段称为边，若规定了路段的方向，则称为弧；边(弧)的权——路段某个或某些特征属性的量化表示。

路权的标定决定了最短的路径搜索依据，也就是搜索指标。根据不同的最优目标，可以选择不同的路段属性。由于舰船上除了平面上的通道之外还有垂直方向的楼梯(或直梯)，如果以最短路程距离作为优化目标，路线的效率未必最高(距离最短未必耗时最少)。所以，以最短行程时间作为优化的目标，道路权重即为各路段的平均行程时间。

对于本文要研究的对象，取各条通道的起点(或终点)和交叉点为图的顶点，各路段为边，路权为路段行走的平均时间。寻找从起点到终点的最短时间路径即为最优路径。在规定了结点、边和权值以后，便将路网抽象为一个赋权无向图或赋权有向图，从而确定路网中某两地间的最优路线便转化为图论中的最短路径问题。

可见，最短路径问题就是一个赋权图的优化问题，简单的数学描述为：P是G中从s到t的一条路(s表示起点，t表示终点)，定义路P的权为W(P)，最短路径问题就是要在所有s到t的路径中求出一条权最小的路径，即求一条从s到t的路径P0，使W(P0)=minW(P)，称P0是从s到t的最短路径。

3 道路权重的标定确定路阻邻接矩阵

3.1 人员迁移流动的特性

国内外对人群流动特性的研究方兴未艾，主要包括交通人流的研究和疏散人流研究的两个方面，他们对人员迁移流动的特性的研究，都是将通道内的人群作为一个整体处理。人流包含一定数目的人员，具有一定的长度与宽度，具有一定的人员密度。不同的密度下，人流具有不同的行走速度。由于舰船的空间普遍紧张，人员分布密度较大，走道楼梯也相对狭窄，特别是在人员奔赴岗位和逃生两种状态下，人员的流动就表现为人群的流动。

与人群的流动相关的概念有：人员密度(单位面积人员的个数)；人的行动速度(单位时间内人行走的距离)；人流速度(人流整体的行进速度)，其值为人流首端的行进速度。在正常状态下， 一般人的行动速度见表1[2]。

表1 人的行动速度

研究证明，一般而言，人流流量= 人流速度×人流密度×通道宽度，而人流速度是人流密度的函数。定性地讲，人流密度越大，人与人之间的距离越小，则人的步行速度越慢，人员移动越缓慢；反之密度越小，人员移动越快。人流密度过大或者过小都会影响步行速度，从而也影响到人流流量的大小。

根据参考文献[3]中，国外的一项实测研究结果表明，人流密度对疏散速度的影响从定量来讲，人群疏散受步幅限制，并得出结论如下：

1) 当疏散通道中，人流密度ρ=1.0人/m2时，则人流迁移流动呈自由流动状态,相应的迁移流动的水平速度为V=1.3 m/s；

2) 当疏散通道中，人流密度ρ=2.0 人/m2时，则人流迁移流动开始呈现滞留流动状态,相应的迁移流动的水平速度为V=0.7 m/s；

3) 当疏散通道中，人流密度ρ= 5.38人/m2时，则人流迁移流动完全处于停滞状态,相应的迁移流动的水平速度为V=0.0 m/s；

4) 在某一密度以下时，密度的提高，随之而产生的速度降低并不明显，但是超过某一密度时，随着密度的提高，速度明显下降。这里的某一密度，是指1.5人/m2左右。

而人流在楼梯中的速度，由参考文献[4]中国外对人流在楼梯中速度的一项实测研究结果表明，一般正常人在不拥挤的楼梯中的行走速度为0.52～0.62 m/s之间；超过65岁的老人在不拥挤的楼梯中的速度为0.43 m/s，而2～5岁的小孩在不拥挤的楼梯中的速度为0.45 m/s。由此可见，楼梯中的人流速度约为水平通道人流速度的二分之一。

表2是人员的行走速度与密度之间的关系[3]。

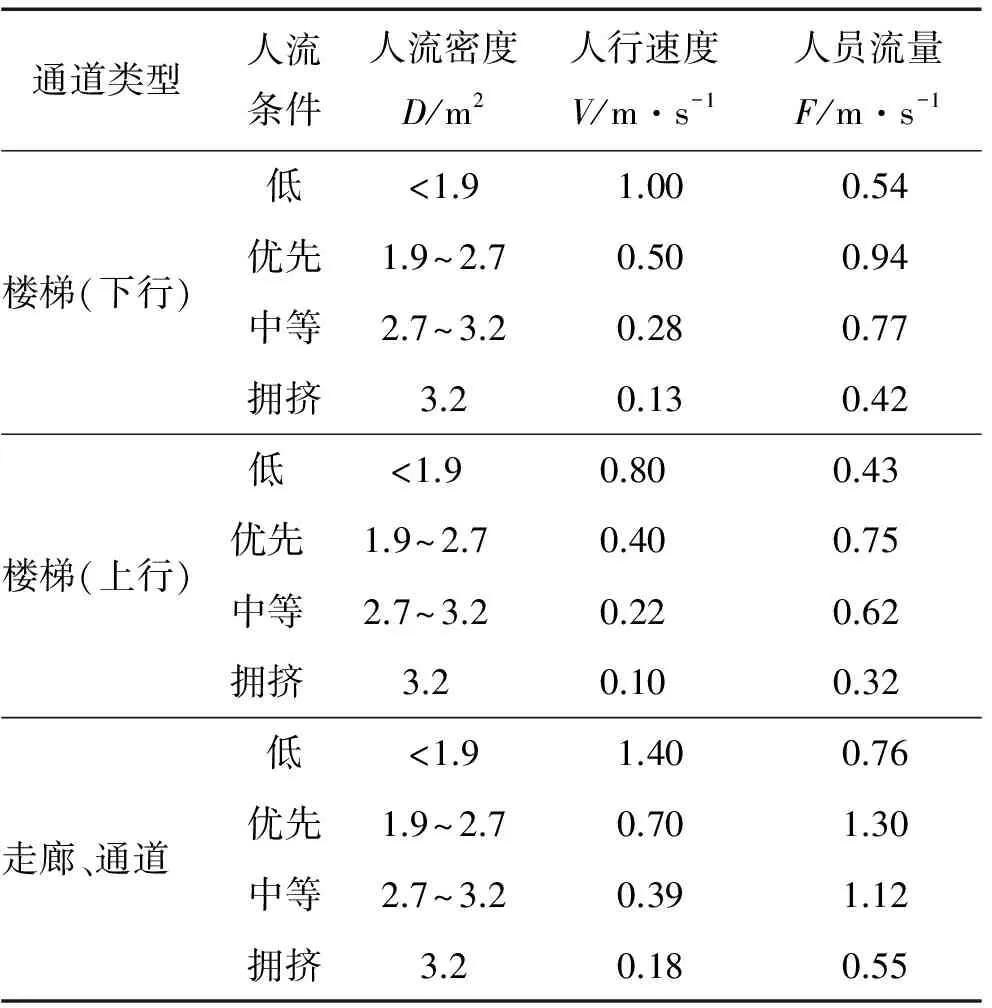
表2 人行速度、密度与流量关系

3.2 路权的确定

参考以上的研究，考虑建筑通道与船舶通道的区别，可以得出如下启示：

1) 舰船上人员奔赴战位时，在平面上行走的密度必须保证人流呈自由流动状态，至少为微滞留状态，这样才能保证行进效率，确保不发生拥堵。其速度范围为1.0～1.4 m/s，取为1.25 m/s;

2) 舰船上楼梯比建筑楼梯要陡，所以参考表2，取上行通过速度和下行速度的折中值为0.6 m/s;

3) 直梯的速度约为0.4 m/s;

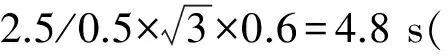
4 算法的实现和应用

确定路网表达方法、存储结构、最优目标、道路权值后，就可以利用赋权有向图的最短路径算法，求解路网中任意出发地到目的地之间的最优路径了。在求解网络图上节点间最短路径的方法中，目前国内外一致公认的较好算法有迪杰斯特拉(Dijkstra)及弗罗伊德(Floyd)算法[5]。这两种算法中，网络被抽象为一个图论中定义的有向或无向图，并利用图的节点邻接矩阵记录点间的关联信息。在进行图的遍历以搜索最短路径时，以该矩阵为基础不断进行目标值的最小性判别，直到获得最后的优化路径。

Dijkstra算法是图论中确定最短路的基本方法，也是其它算法的基础。为了求出赋权图中任意两结点之间的最短路径，通常采用两种方法。一种方法是每次以一个结点为源点，重复执行Dijkstra算法n次。另一种方法是由Floyd于1962年提出的Floyd算法，其时间复杂度为O(n3),虽然与重复执行Dijkstra算法n次的时间复杂度相同，但其形式上略为简单，且实际运算效果要好于前者。

4.1 图的建立

首先将空间问题抽象为图，图1为某舰的两层甲板的部分抽象图，上下两个平面上纵横交错的直线为各层甲板的主要通道，连接两层甲板的直线表示楼梯，包括2个直梯和3个斜梯。每条路段上的标注(a,b)中，a表示路段实际长度或者楼梯的类型，m;b表示此路段的行程时间(即路权)，s如(40，32)。

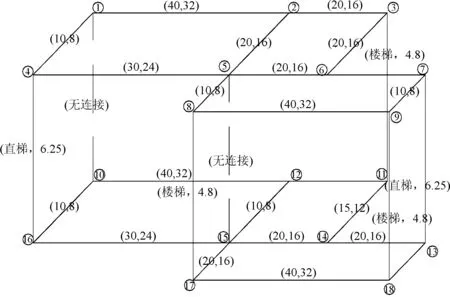
图1 两层甲板的部分抽象图

按照图的定义建立如下所示的赋权图，见图2。

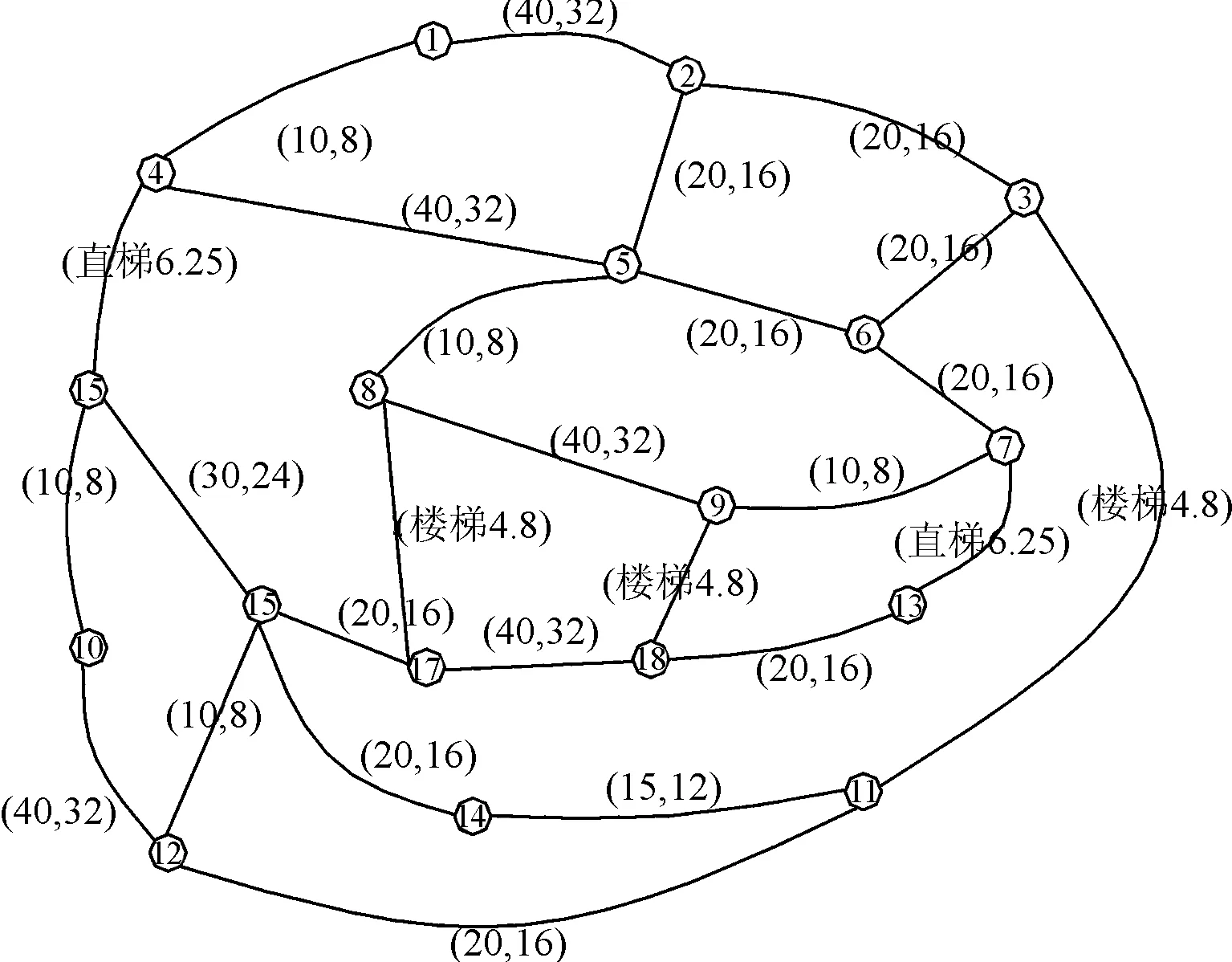
图2 赋权图

4.2 确定路阻矩阵

根据赋权图建立路阻矩阵:

则有D=

[2]1234567891011121314151617181032in8infinfinfinfinfinfinfinfinfinfinfinfinfinf 232016inf16infinfinfinfinfinfinfinfinfinfinfinfinf 3inf16016infinfinfinfinfinf4．8infinfinfinfinfinfinf 48infinf024infinfinfinfinfinfinfinfinfinf6．25infinf 5inf16inf24016inf8infinfinfinfinfinfinfinfinfinf 6infinf16inf16016infinfinfinfinfinfinfinfinfinfinf 7infinfinfinfinf1608infinfinfinf6．3infinfinfinfinf 8infinfinfinf8infinf032infinfinfinfinfinfinf4．8inf 9infinfinfinfinfinf8320infinfinfinfinfinfinfinf4．8 10infinfinfinfinfinfinfinfinf0inf32infinfinf8infinf 11infinf4．8infinfinfinfinfinfinf016inf8infinfinfinf 12infinfinfinfinfinfinfinfinf32160infinf8infinfinf 13infinfinfinfinfinf6．25infinfinfinfinf0infinfinfinf16 14infinfinfinfinfinfinfinfinfinf8infinf016infinfinf 15infinfinfinfinfinfinfinfinfinfinf8inf1602416inf 16infinfinf6．25infinfinfinfinf8infinfinfinf240infinf 17infinfinfinfinfinfinf4．8infinfinfinfinfinf16inf032 18infinfinfinfinfinfinfinf4．8infinfinf16infinfinf320

4.3 运用Floyd算法确定最短路径

Floyd算法的功能是通过一个图的路权矩阵求出每两点之间的最短距离，这种算法的优点是容易理解，可以算出任意两点间的最短路径；缺点是其复杂度为三次方，不适合大量的数据处理。

Floyd算法的基本原理和实现方法为：如果一个矩阵D=[dij],其中dij>0表示i与j间的距离，若i与j间无路可通，则dij为无穷大。i与j间的最短距离存在经过i与j间的k和不经过k两种情况，所以可以令k=1，2, 3，……，n(n为节点数)。检查dij与dik+dkj的值，在此，dik与dkj分别为目前所知的i到k与k到j的最短距离，因此，dik+dkj就是i到j经过k的最短距离。所以，若有dij>dik+dkj,就表示从i出发经k再到j的距离要比原来的i到j距离短，自然把i到j的dij重写成dik+dkj。每当一个k搜索完，dij就是目前i到j的最短距离。重复这一过程，最后当查完所有k时，dij就为i到j的最短距离。

运用Matlab编程工具编写的程序，其核心代码如下：

……

for k=1:n

for i=1:n

for j=1:n

if D(i,k)+D(k,j)

D(i,j)=D(i,k)+D(k,j);%修改长度

path(i,j)=path(i,k);%修改路径

end

end

end

……

选取任意两点输入Matlab程序运行，可得到两点间最短路径。举几个实例见表3。

表3 计算结果

5 总结与设想

运用经典的图论算法确定最短路径的这种方法，是舰船通道线路优化设计的基础，本文提取简化的舰船通道线路模型，参考流量理论建立赋权图，运用合适的算法能够求得网络图中任意两点间的最优路径。对于船舶特别是对大型舰船，或者甲板层数多、路线复杂并且人员密度大的舰船，合理的路线设计具有重要的现实意义，本文的方法对舰船通道设计路线优化技术的研究起到了基础性的作用。

本文的研究是建立在简化模型的基础上，实际的情况可能更复杂，未来还有许多值得研究和探讨的问题，比如：

1) 流动的人群在移动的过程中表现为具有相互联系的三种状态:集结、流动、滞留状态。而滞留常常发生在舱室的开口部位，如房间的出口、楼梯的入口等位置。本文假设所有的人群都是自由流动的，这与实际情况并不完全符合。所以，在最短行程时间路径的确立上能否考虑滞留时间，或者能否预测滞留地点，或者提出带流量控制权值或考虑道路通行能力的图论方法，建立一个多目标优化的数学模型；

2) 最短路径也许并不是最优路径，在许多点上的人群一起移动时，最短路径的某些地段可能出现拥堵，这样就必须考虑选择次优路径的问题；

3) 对甲板层数多或者路线复杂的通道网络，如果采用人工标点来建立网络，这会是一个非常烦琐的工作，而且如果网络过于复杂，经典的图论算法就需要作一些改进；

4) 能否借鉴智能交通系统(比如地理信息系统(GIS)和智能运输系统(ITS))对交通实时诱导的相关理论，建立船舶道路系统的数据库和路网结构，在此基础上实现智能搜索最优及次优路径，这些都是以后需要研究的问题[6]。

[1] 戴文舟.交通网络中最短路径算法的研究[D].重庆大学硕士学位论文，2004.

[2] PROUHX G.Evacuation time and movement in apartment buildings[J]. Fire Safety Journal,1995(24):229-246.

[3] 谢灼利，等.地铁车站站台火灾中人员的安全疏散[J].中国安全科学学报，2004，14(7)：21.

[4] 建筑防火设计与应用[M].中国建筑学会防火综合技术委员会.北京:海洋出版社,1991.

[5] 王平.大型公共建筑人员疏散性能化评估软件的开发.武汉大学硕士学位论文[D]，2005.

[6] 荣玮.基于道路网的最短路径算法的研究与实现.武汉理工大学硕士学位论文[D]，2005.