随机斜浪中船舶参数—强迫激励横摇运动计算

1 引 言

1955年,Kerwin首次提出船舶在纵浪中航行,船体交替处于波峰和波谷，船体浸水部分的形状和体积随时间变化，使得船舶初稳性高也随时间变化，是导致纵浪中船舶横摇运动失稳及倾覆的重要原因[1]。随后很多学者都对随机和规则纵浪中船舶的纯参数激励横摇运动进行了大量研究。但是，对船舶在遭受参数激励和横向强迫激励(以下简称为“参—强激励”)下的动力学特征，研究较少。我们建立并用多尺度法求解了规则参—强联合激励的横摇运动方程[2]。船舶遭受随机参—强激励包括了船舶运动的更广泛的航行背景，然而对此项问题的研究还鲜见报道。本文考虑船舶横摇恢复力矩的非线性和波浪的随机性，假设升沉和纵摇准静力平衡，将随机参数激励引入横摇方程，采用Dunwoody方法推导由波浪引起的随机初稳性高波动项[3]，得到了参—强激励横摇运动的计算方法。考虑不同航速、航向、波高、波长对某渔政船进行了参—强激励横摇计算。

2 参—强激励方程

考虑阻尼力矩和恢复力矩的非线性，以及升沉、纵摇、波浪共同作用产生的参数激励和强迫激励项建立的横摇运动方程如下：

(1)

阻尼力矩取线性加立方阻尼的形式：

(2)

恢复力矩是横摇、升沉、纵摇、波面升高及时间的函数：

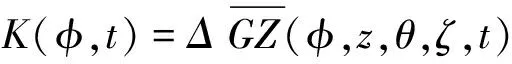
(3)

式中，回复力臂可以用下式表示：

(4)

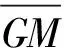
3 随机斜浪中船舶横摇干扰力矩和初稳性高的计算

将随机波表示为一系列简谐波的叠加，干扰力矩公式为[4]：

(5)

式中，I为考虑了附加质量的横摇转动惯性矩；α0为波倾斜系数；ω0为横摇的固有频率；hi是分谐波波高；λi是分谐波波长；χ是航向角；ωei是船舶斜浪航行的船波遭遇频率；εi为在区间(0～2π)内均匀分布的随机相位角。

船舶斜浪航行过程中，波浪除了对船舶施加以横摇扰动力矩外，还引起了船舶横摇初稳性高的变化。船舶左右两舷的波面差产生了横摇扰动力矩，本文根据船长x处的平均波面升高来计算初稳性高。随机斜浪中沿船舶表面的波面升高表达式见式(6)。它不仅同时间t、遭遇频率ωe、随船坐标系纵向坐标x有关，还与横向坐标y有关。船体表面 (x,y)点的波面升高为：

(6)

式中，hi为分谐波波幅；ki为分谐波波数；χ为航向角；χ=0°表示迎浪航行状态；ωi为分谐波波浪圆频率；λi为分谐波波长；U为船速。

在船长纵向坐标x处，左右两舷的波面升高分别为：

cos[ki(xcosχ-ylsinχ)+ωeit]

(7)

cos[ki(xcosχ-yrsinχ)+ωeit]

(8)

因为船舶左右对称yl=-yr，所以x处的平均波面升高为：

cos(kixcosχ+ωeit)cos(kiylsinχ)

(9)

采用Dunwoody方法得到由波浪引起的随机初稳性高波动项gm(t)的表达式：

(10)

(11)

(12)

(13)

考虑随机波浪为一系列简谐波的叠加，得到波面升高加速度的表达式。

cos(kixcosχ+ωeit)cos(kiylsinχ)

(14)

将式(9)和式(14)代入式(10)，可计算初稳性高波动值，由式(1)可计算横摇角的响应历程。

4 参—强激励算例分析

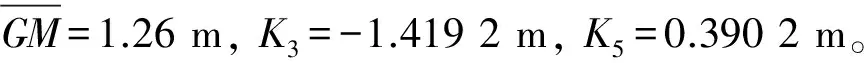
取随机波浪特征波长λ=40 m，有义波高h1/3=3 m，波浪的特征频率为1.24 rad/s，特征周期为5.1 s；航向30°，首斜浪航行航速7.492 8 m/s，特征遭遇频率为2.26 rad/s，为横摇固有频率的2倍，得到的初稳性高谱、横摇扰动力矩谱，考虑和不考虑初稳性高变化的随机横摇运动结果见图1～图6。

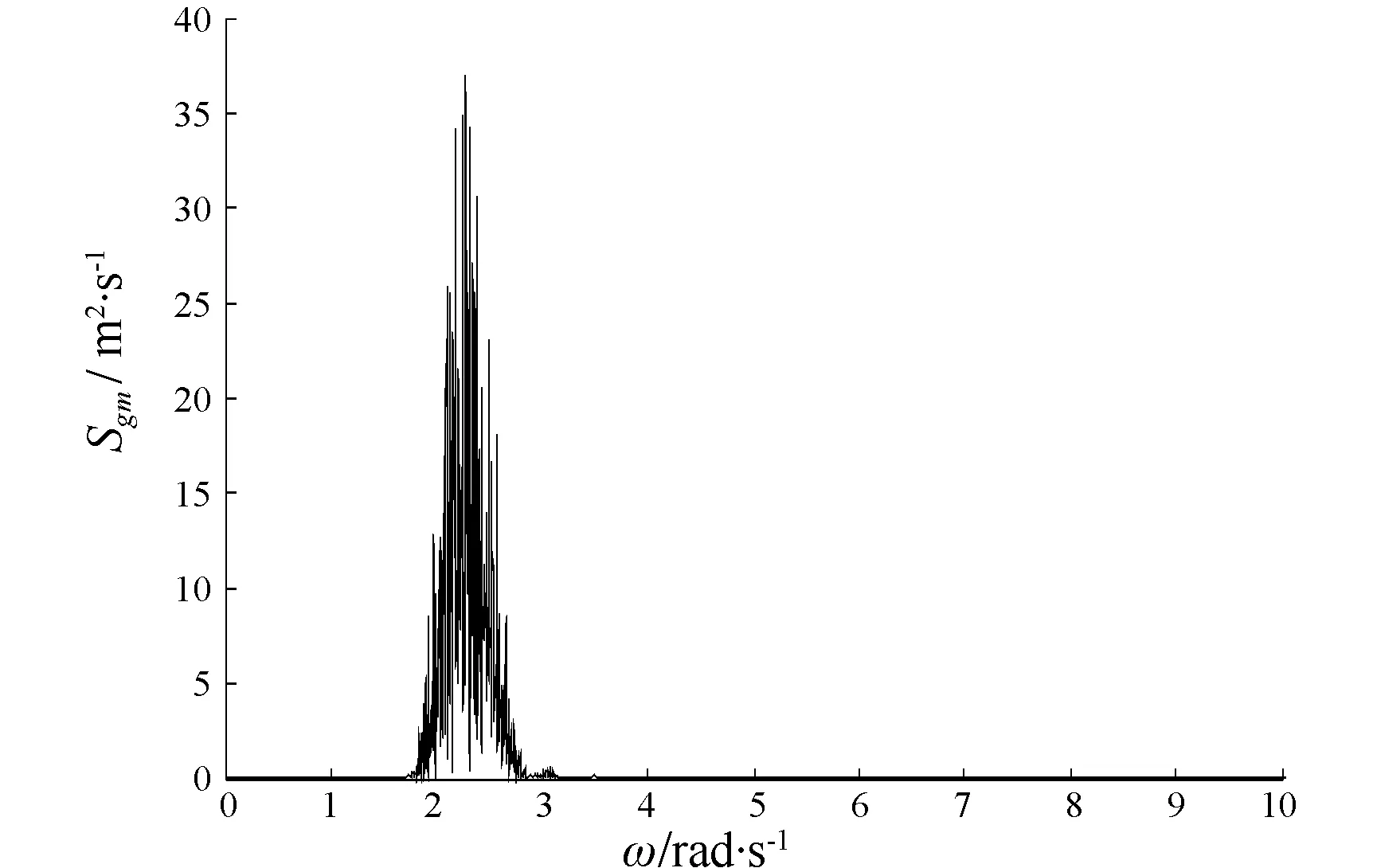
图1 初稳性高谱

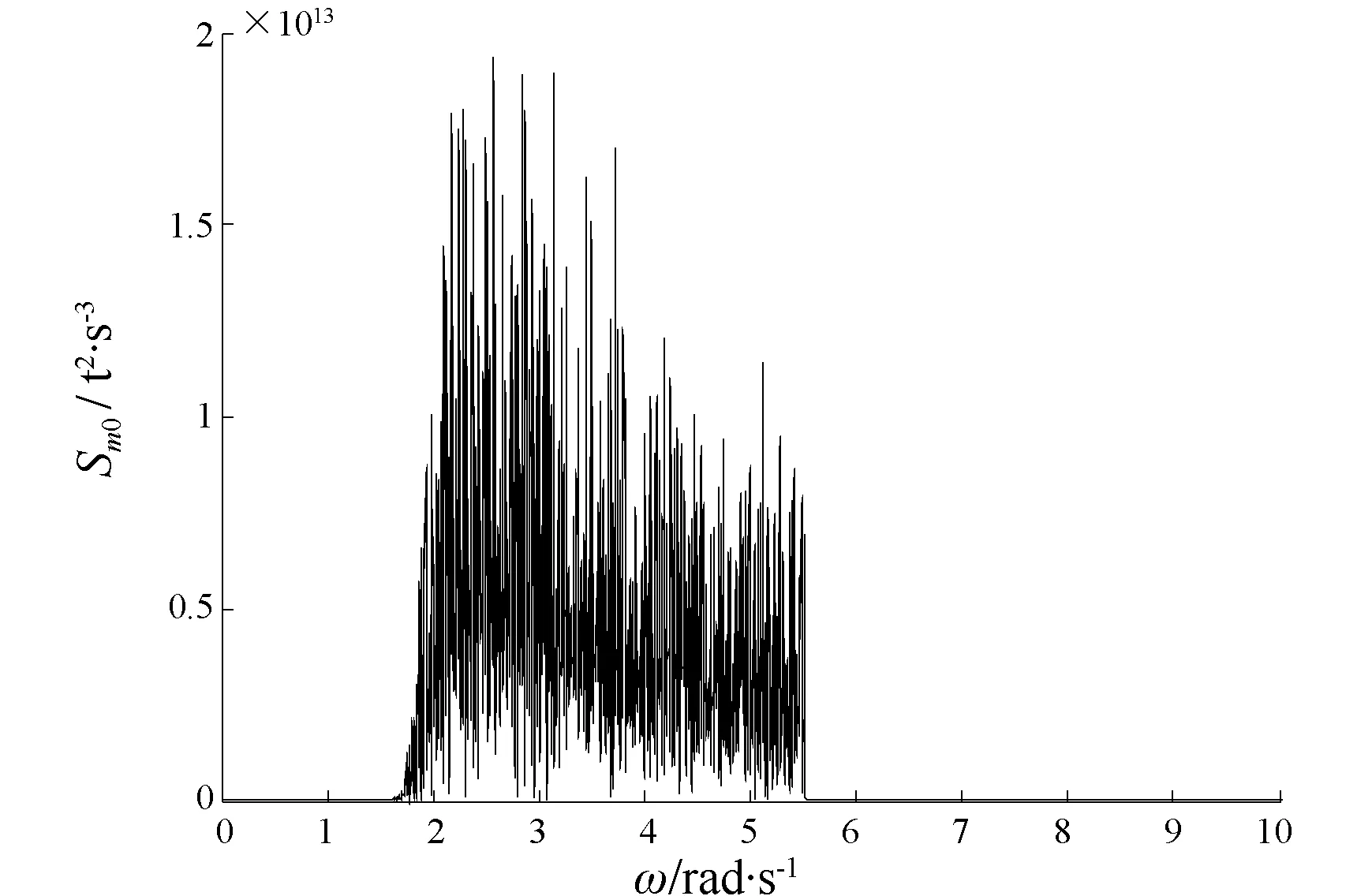
图2 横摇干扰力矩谱

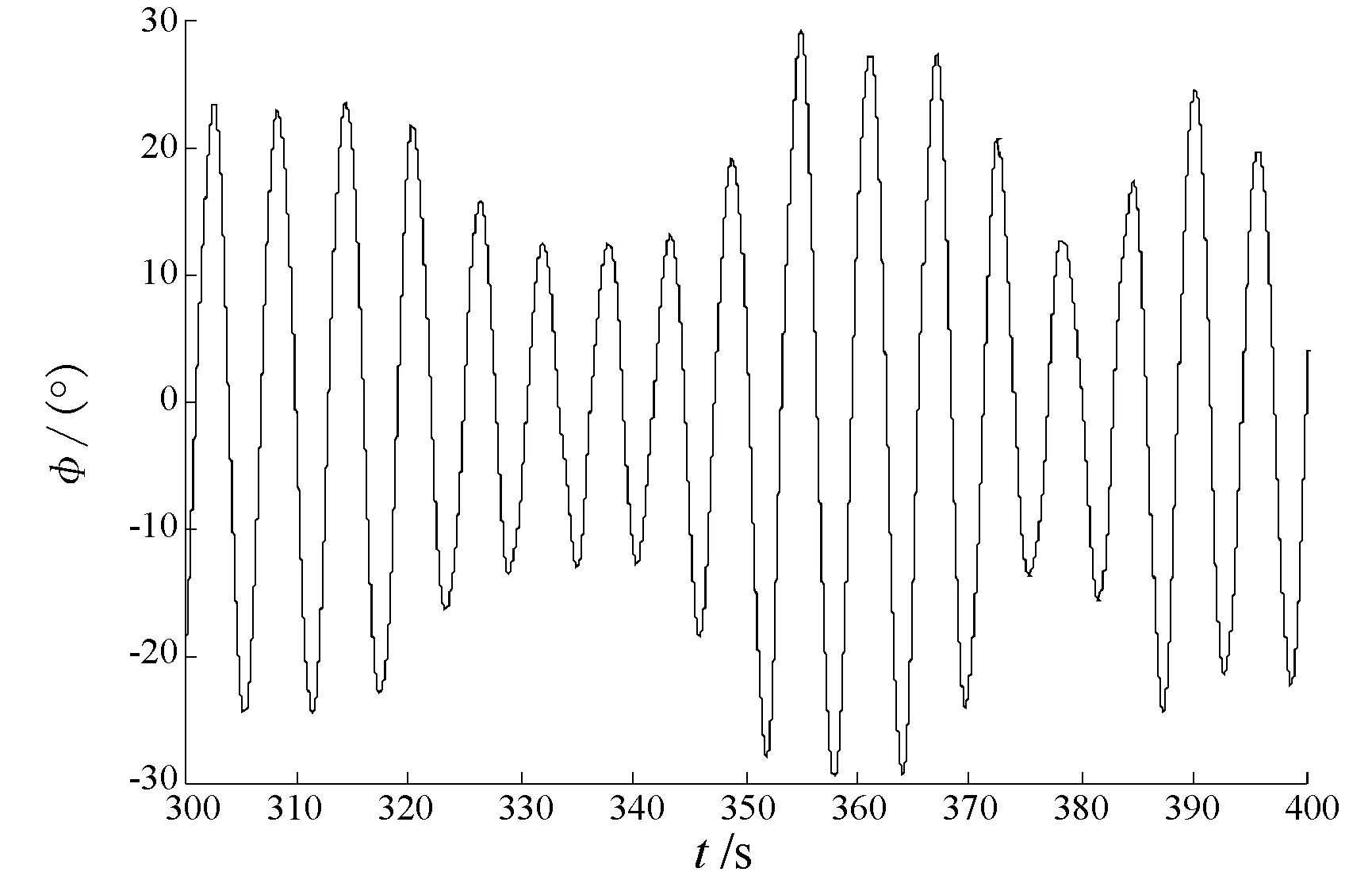
图3 横摇角(考虑初稳性高的变化)

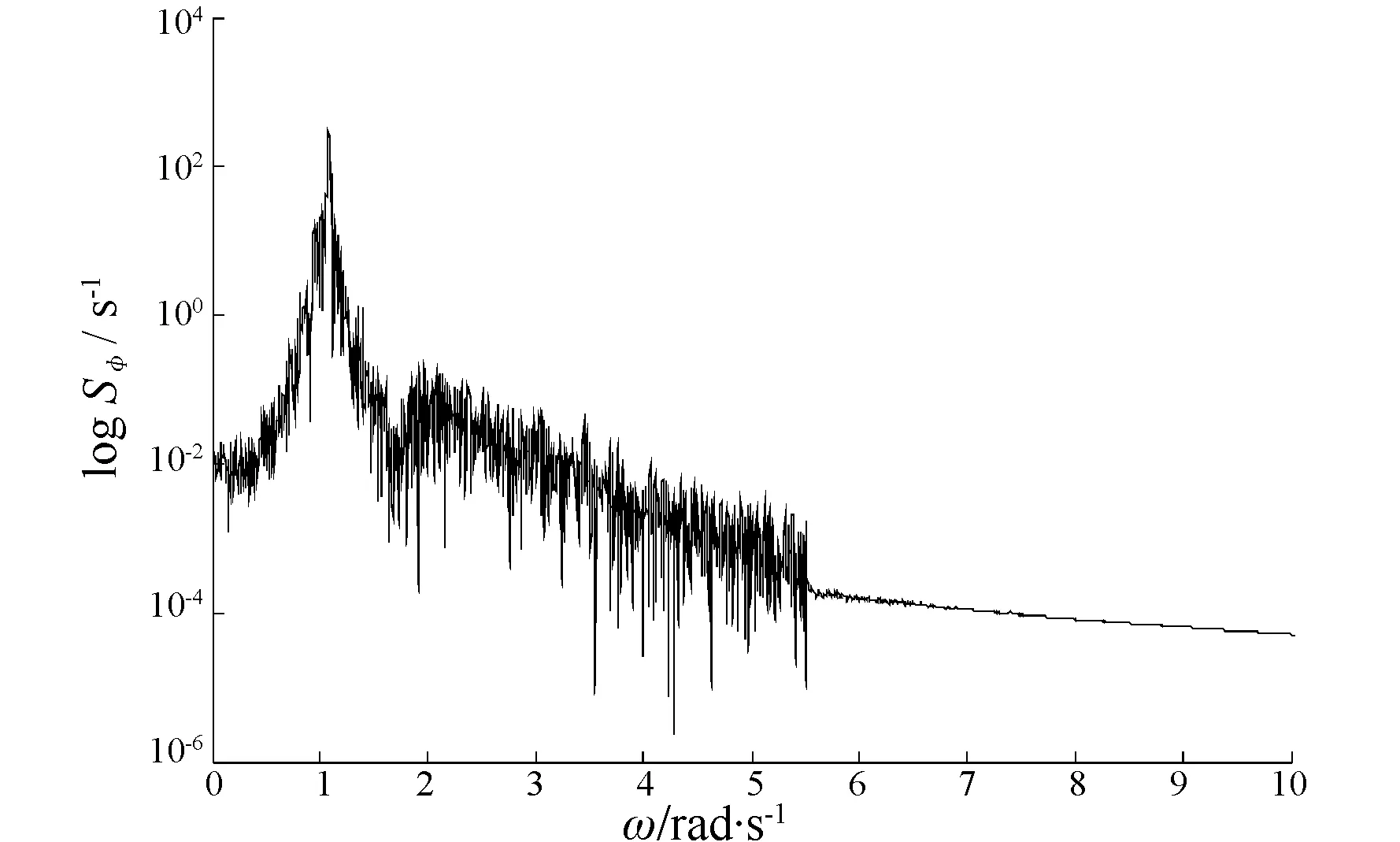
图4 横摇角谱(考虑初稳性高的变化)

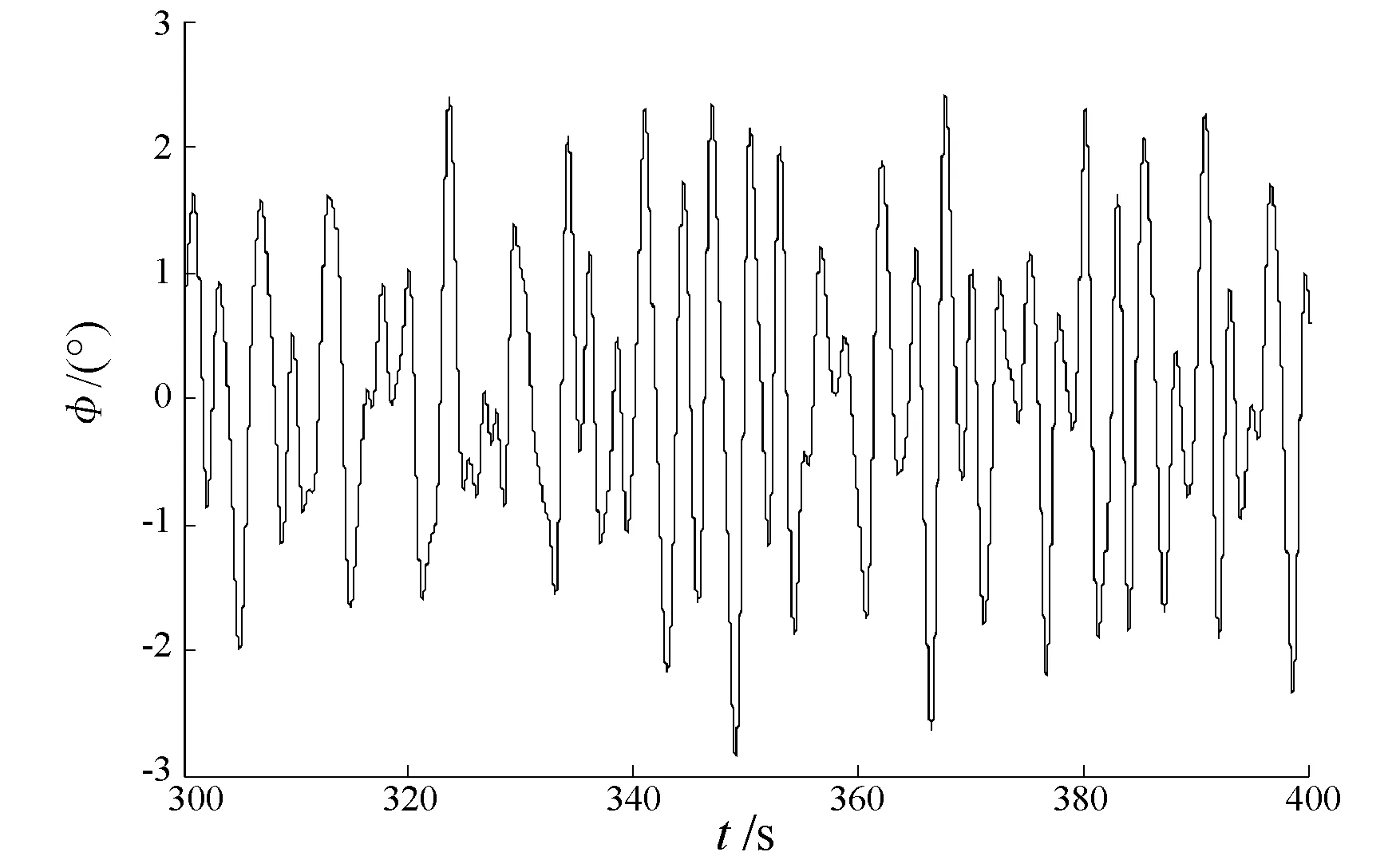
图5 横摇角(不考虑初稳性高的变化)

图6 横摇角谱(不考虑初稳性高的变化)

取随机波浪特征波长λ=40 m，有义波高h1/3=3 m，波浪的特征频率为1.24 rad/s，特征周期为5.1 s;航向30°，航速U分别取1 m/s, 2 m/s,……,12 m/s。按照上述方法计算得到的稳定横摇的最大幅值的变化如图7所示。在图7～图10中，“*”表示考虑参数激励及波浪外激励的影响计算得到的最大横摇角，“△”表示不考虑参数激励的影响，仅计入波浪外激励得到的结果。

取随机波浪特征的波长λ=40 m，有义波高h1/3=3 m，波浪的特征频率为1.24 rad/s，特征周期为5.1 s，保持遭遇特征频率为横摇固有频率的2倍；航向角分别取0°, 5°,……, 60°。按照上述方法计算得到的稳定横摇的最大幅值的变化如图8所示。因为波浪扰动力矩的频率远离横摇外激励共振区域，所以波浪扰动力矩对横摇的影响不大，而参数激励特征频率为横摇固有频率的2倍，位于主参数共振区域，对横摇影响很大。

图7 最大横摇角随航速的变化

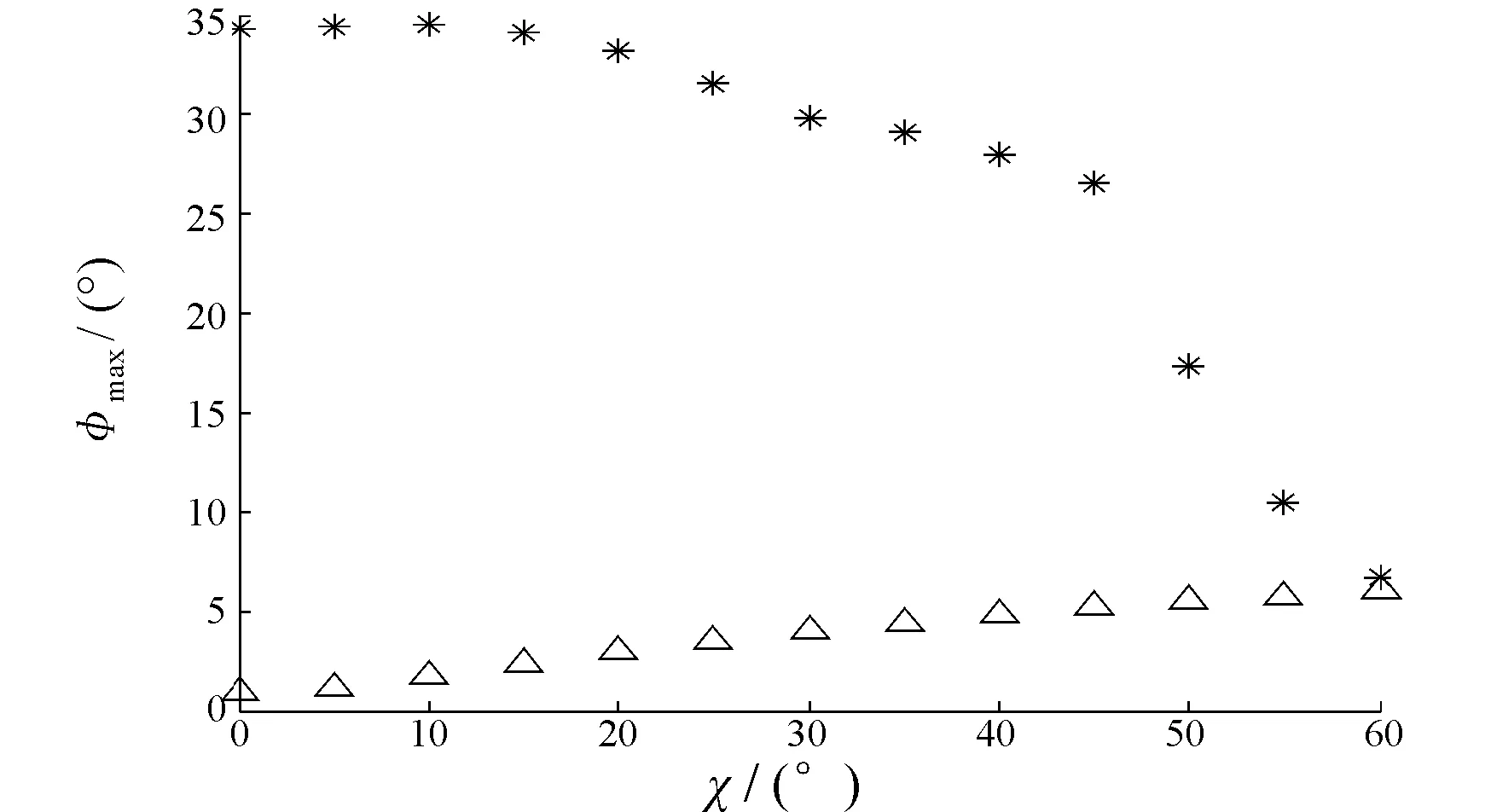
图8 最大横摇角随航向的变化

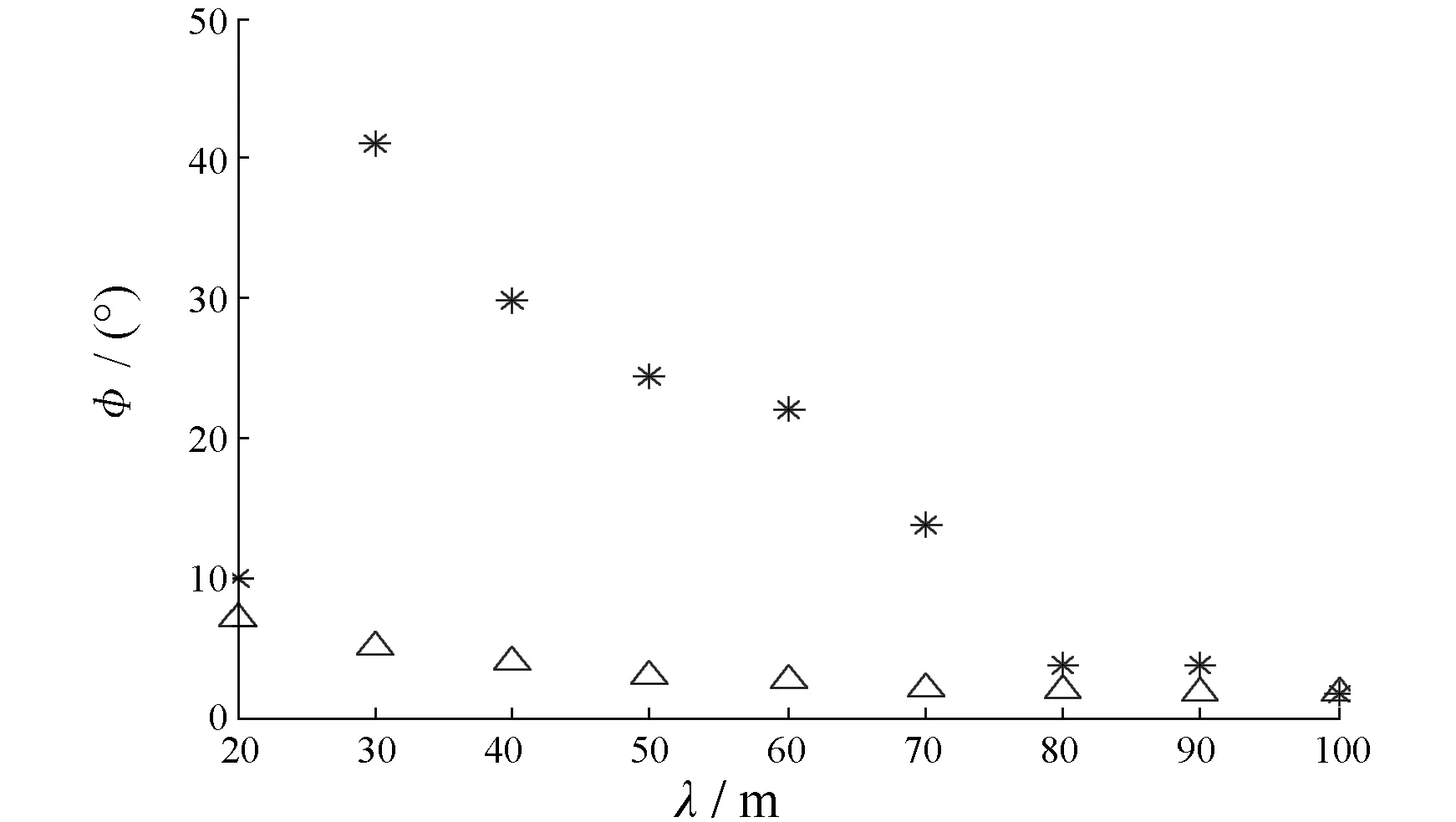
图9 最大横摇角随波长的变化

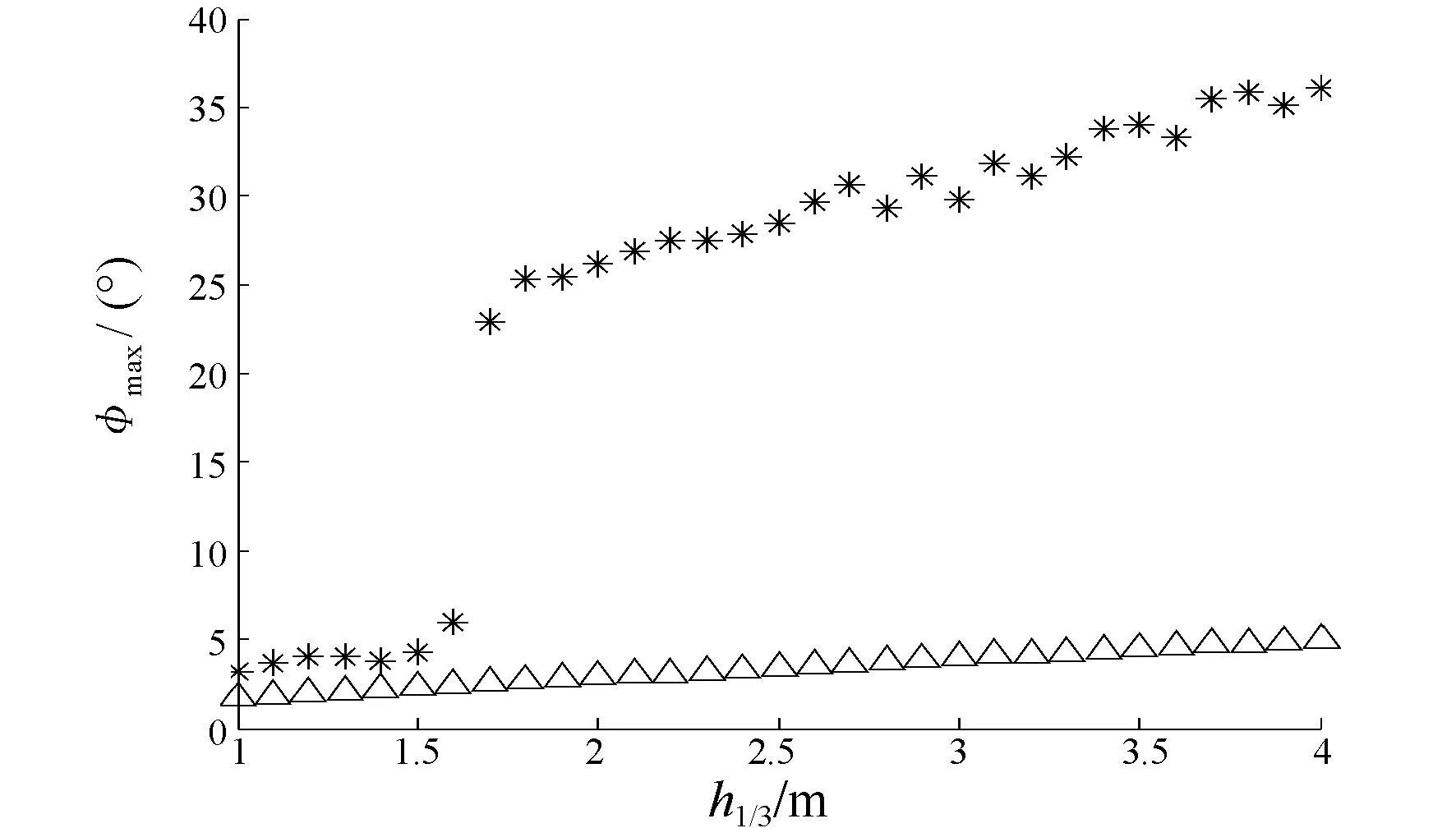
图10 最大横摇角随波高的变化

取随机波浪有义波高h1/3=3 m，保持遭遇特征频率为横摇固有频率的2倍；波长分别取20 m, 30 m,……, 100 m。按照上述方法计算得到的稳定横摇的最大幅值变化如图9所示。由此可见，在λ/cosχ与船长相差不大时，参数激励对横摇的影响较明显。而对于外激励而言，波陡越大，横摇扰动力越大，相应的横摇幅值就越大。

取随机波浪特征波长λ=40 m，波浪的特征频率为1.24 rad/s，特征周期为5.1 s，航向30°，保持遭遇特征频率为横摇固有频率的2倍；有义波高分别取为h1/3=1 m,1.25 m,……，4 m。按照上述方法计算得到的稳定横摇的最大幅值的变

化见图10。从图10中可见，参数激励和外激励引起的横摇运动都随着波高的增大而增大，只有当波高超过某一阈值时，参数激励横摇才可能被激起。

5 结束语

经过上述计算得到的分析结论如下：

1) 对于随机斜浪中的参—强激励横摇运动，当特征遭遇频率一定时，最大稳定横摇幅值随波高的增大而增大，随航向角的增大而减小。

2) 对于随机斜浪中的参—强激励横摇运动，当特征遭遇频率为船舶横摇固有频率的2倍时，因为波浪扰动力矩谱能量是在横摇固有频率的2倍附近，远离共振区域，所以它对横摇的影响非常小，而因为参数激励谱能量集中在主参数共振频率(即2倍横摇固有频率)附近，所以它对横摇起决定性作用。

3) 对于不规则波中的横摇，由算例结果可见，在航向角和不规则波的特征波长、有义波高、特征频率确定的时候，随着遭遇频率由2倍横摇固有频率向1倍横摇固有频率变化，参数激励对船舶的影响逐渐减小，而波浪扰动力矩对船舶横摇的影响逐渐增大。在计算斜浪中变航速的横摇响应时，两者都要考虑。

[1] KERWIN J E.Notes on rolling in longitudinal waves[J].International Shipbuilding Progress，1955，2(16)：597-614.

[2] 唐友刚，林维学，董艳秋.船舶参数激励和强迫激励作用下的非线性运动响应[J].中国造船，2001，42(6)：34-39.

[3] DUNWOODY A B. Roll of a ship in astern seas-metacentric height spectra[J]. Journal of Ship Research, 1989, 33(3):221-228.

[4] Intact Stability Criteria for Passenger and Cargo Ship[S], IMO, 1987.

[5] Jianbo Hua.A study of the parametrically excited roll motion of a RoRo-ship in following and heading waves[J].International Shipbuilding Progress，1992，39(420)：345-366.