复合材料螺栓连接结构数值模拟研究
2008-04-24佘凯,许建,黄国兵等
1 引 言
复合材料是由两种或多种不同性质的材料用物理和化学方法在宏观尺度上组成的具有新性能的材料,其具有重量轻、比强度高、抗疲劳性能强、耐腐蚀等优点,在航空航天、汽车、造船等各个领域得到日益广泛的应用[1]。船舶是复合材料应用中的一个重要方面,经多年的开发使用,应用部位已从次承力构件发展到主承力构件,逐步成为一种重要的船用材料。复合材料与金属构件常采用螺栓连接,由于复合材料挤压强度较低,结构在承受较大载荷时,连接部位螺孔处的复合材料会发生挤压破坏,是该结构的主要破坏模式。
复合材料结构的连接在传递载荷、连接件的形态和边界条件等方面都比较复杂,用解析方法求解是难以胜任的,需要采用数值方法特别是可用有限元法来求解。
复合材料螺栓连接是一个三维问题,国外已经采用多种有限元软件对其进行了数值模拟。GRUTTA等[2]采用ABAQUS软件对弯矩作用下的层合板螺栓连接接头强度进行了分析。CAMANHO等[3]采用三维有限元模型,利用ABAQUS软件对层合板螺栓连接接头的损伤进行了预测。NGUYEN[4]在SAMCEF程序中引入三维有限元模型,对含孔复合材料层合板的损伤破坏进行了分析。LIN等[5]采用MARC有限元分析软件,考虑到多孔对接头的影响,对单搭接的层合板接头强度进行了分析。TONG[6]针对不同的端部约束,对双搭接接头的挤压失效问题进行了研究。MORAIS[7]提出了分析准各向同性含孔层合板拉伸强度的二维、三维混合有限元模型。分析表明,在孔附近,易采用精细的三维单元;而远离孔处可采用二维单元进行分析。GONG等[8]采用三维有限元分析技术,对扭矩作用下的含缺口的层合板的初始损伤进行了预测分析。
采用有限元法时,对复合材料、螺栓、连接件之间采用何种边界处理方式会对数值结果和计算时间产生较大影响[9]。一是考虑螺栓与其连接结构存在接触的边界条件下,用连续结构单元进行网络划分,不但可以使有限元模型准确,还可精确得到螺栓连接结构的应力、载荷分布,但是模型较为复杂,容易造成过长的计算机时;二是对螺栓结构进行简化或采用耦合自由度的方法来描述螺栓的连接关系,可以大量节约计算机资源,提高计算效率,但是计算结果的准确性稍差一些。
本文以试验中的复合材料螺栓连接结构为研究对象,应用ANSYS有限元软件分别建立了采用不同边界处理方式的有限元模型,对复合材料螺栓连接结构的强度进行数值模拟,给出了数值计算结果并对结果进行了分析,总结出了各种边界处理方式对数值模拟结果的影响。
2 计算模型
根据试验中的复合材料壳板、连接工装等结构进行实体建模,对不同材料、属性的模型赋予单元类型及实常数,并对其划分网格,采用不同的边界处理方式对结构进行加载求解。
2.1 几何模型
复合材料连接结构如图1所示,图2为复合材料壳板,图3为907钢板(连接工装),图4为连接结构详图,本文中将所有18个螺栓简化为圆柱体。

图1 复合材料连接结构图
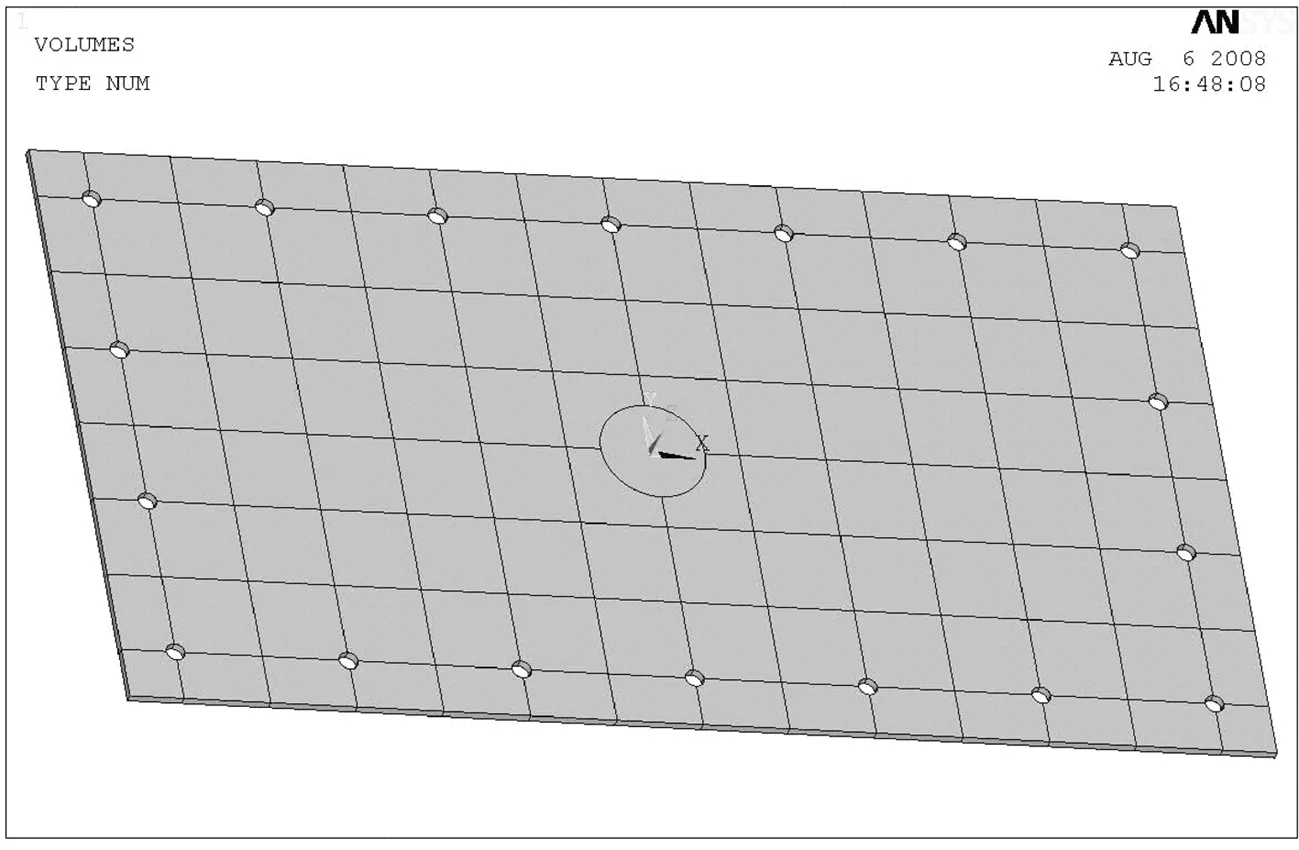
图2 复合材料壳板

图3 907钢板(连接工装)
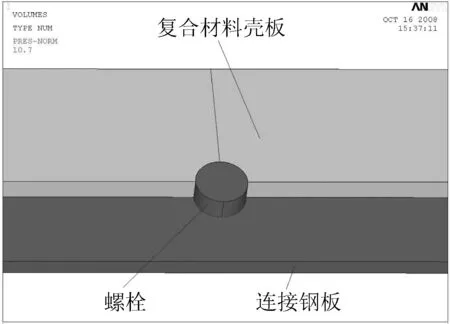
图4 连接结构详图
2.2 接 触
接触问题属于不定边界问题即边界条件非线性问题,即使是简单的弹性接触问题也具有非线性,其中既有由接触面积变化而产生的非线性以及由接触压力分布变化而产生的非线性,也有由摩擦作用产生的非线性。这种非线性和边界不定性的接触问题求解是一个反复迭代的过程。
对于接触问题,除了其场变量需要满足固体力学基本方程以及相应的定解条件外,还必须满足接触面上的接触条件。接触条件主要包括两个方面,一是接触体之间在接触面上的变形协调性,不可相互侵入;二是摩擦条件。
对于接触或将要接触的两个物体,其界面接触状态可以分成分离、粘结接触和滑动接触三种。对于这三种情况,接触界面的位移和力的条件是各不相同的,而实际的接触状态又往往在这三种状态间相互转化,从而导致接触问题的高度非线性特点。
由于接触问题是一种高度非线性行为,需要较大的计算资源。接触问题存在两个较大的难点:其一,在求解问题之前,不知道接触区域表面之间是接触还是分开的,或是突然变化的,这要随载荷、材料、边界条件和其它因素而定;其二,大多数接触问题需要计算摩擦,摩擦使问题的收敛性变得困难。
接触问题分为两种基本类型:刚体—柔体的接触和柔体—柔体的接触。在刚体—柔体的接触问题中,接触面的一个或多个被当作刚体,与它接触的变形体相比,有大得多的刚度。一般情况下,一种软材料和一种硬材料接触时,问题可以被假定为刚体—柔体的接触,许多金属成形问题归为此类接触。另一类,柔体—柔体的接触,是一种更普遍的类型,在这种情况下,两个接触体都是变形体,具有近似的刚度[10]。
本文的研究对象中有三种接触关系:螺栓与复合材料壳板孔、连接钢板与复合材料壳板、螺栓与连接钢板。螺栓、复合材料壳板、连接钢板这三者的刚度相差不大,这三种接触关系都归为柔体—柔体的接触。
2.3 耦 合
当需要迫使2个或多个自由度取得相同值时,可以将这些自由度耦合在一起。所有耦合节点将强迫其在指定的节点座标系方向上有同样的位移值。耦合自由度集包含1个主自由度和1个或多个其它自由度[11]。
典型的耦合自由度应用包括:
1) 模型部分包含对称;
2) 在两重复节点间形成销钉、铰链、万向节和滑动连接;
3) 迫使模型的一部分表现为刚体。
本文中采用耦合节点的方式近似代替接触关系,将螺栓与复合材料壳板孔、连接钢板与复合材料壳板、螺栓与连接钢板的相互接触面上的节点耦合,通过耦合不同方向的自由度,迫使节点在该方向上产生相同的位移,而在其它未被耦合的方向上仍有相对位移。
2.4 模型单元类型与材料属性
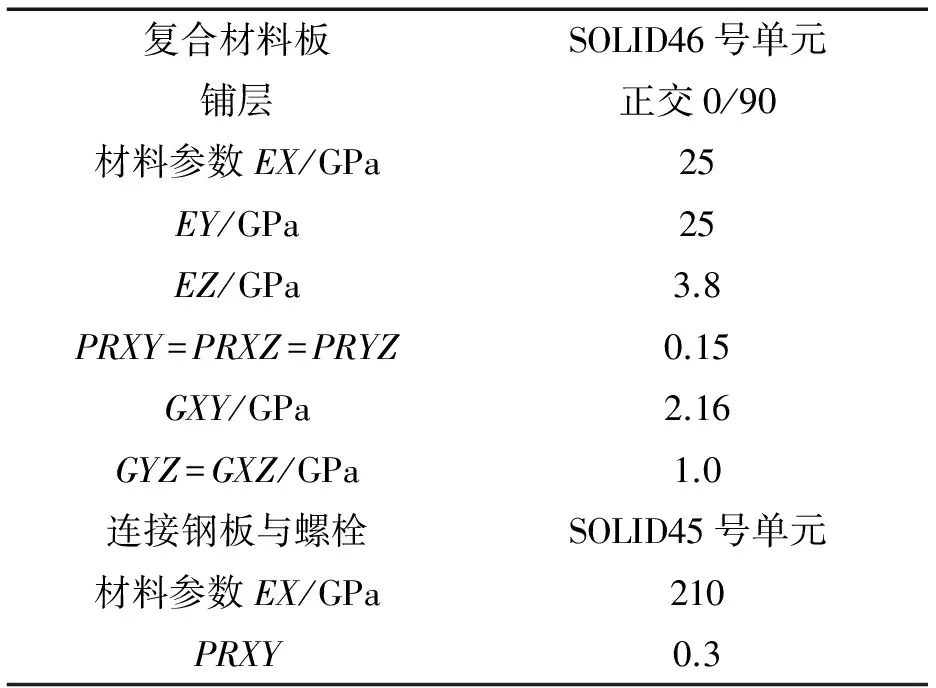
表1 模型单元类型与材料属性
2.5 有限元模型
为了使计算结果精确并节约计算机运算资源,只在每个螺栓孔处将网格细化,如图5、图6所示。

图5 复合材料连接结构有限元模型
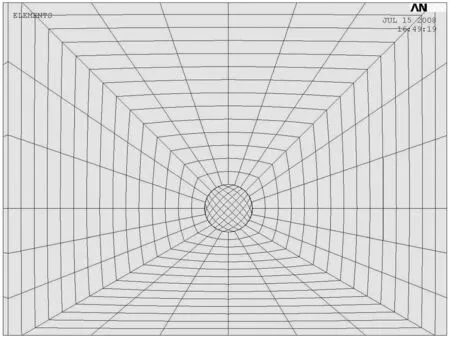
图6 螺栓孔处网格划分
2.6 边界处理方式
方式一:将螺栓与复合材料壳板孔、复合材料壳板与连接钢板、螺栓与连接钢板之间按接触关系处理,建立接触对,摩擦系数取为0.2。
方式二:将螺栓与复合材料壳板孔之间按接触关系处理,建立接触对,摩擦系数为0.2;采用耦合重合节点的方式连接复合材料壳板与连接钢板,耦合Z方向的自由度;螺栓与连接钢板耦合X、Y、Z方向的自由度连接为一体。
方式三:将螺栓与复合材料壳板孔之间按接触关系处理,建立接触对,摩擦系数为0.2;将复合材料壳板与连接钢板、螺栓与连接钢板利用耦合重合节点的方式连接为一体,耦合X、Y、Z方向的自由度。
方式四:不考虑接触,将螺栓与复合材料壳板孔、复合材料壳板与连接钢板、螺栓与连接钢板利用耦合重合节点的方式连接为一体,耦合X、Y、Z方向的自由度。
方式五:将螺栓与复合材料壳板孔之间按接触关系处理,建立接触对,摩擦系数为0.2;建模时将螺栓与连接钢板合并为一个结构,将连接钢板与复合材料壳板利用耦合重合节点的方式连接,耦合Z方向的自由度。
方式六:将螺栓与复合材料壳板孔之间按接触关系处理,建立接触对,摩擦系数为0.2;建模时将螺栓与连接钢板合并为一个结构,将连接钢板与复合材料壳板利用耦合重合节点的方式连接为一体,耦合X、Y、Z方向的自由度。
2.7 约束及载荷工况
试验中在复合材料壳板表面中部施加了半径为50 mm的圆面均布载荷,载荷逐渐增大直至钉孔连接部位刚好发生破坏,此时载荷大小为10.7 MPa。采用ANSYS进行加载和约束时,将连接工装的底部刚性固定,并约束所有螺栓底面X、Y、Z三个方向的自由度;在复合材料壳板表面中部施加半径为50 mm的圆面均布载荷,大小为10.7 MPa,如图7所示。

图7 加载工况
3 计算结果及比较
试验中该复合材料壳板最先发生钉孔破坏位置为距离加载位置最近的2个孔:沿长度方向(X方向)第4个钉孔处。测得该孔所承受挤压载荷Fy为40 kN。表2列出了6种边界处理方式受载后该钉孔处Fy的大小。
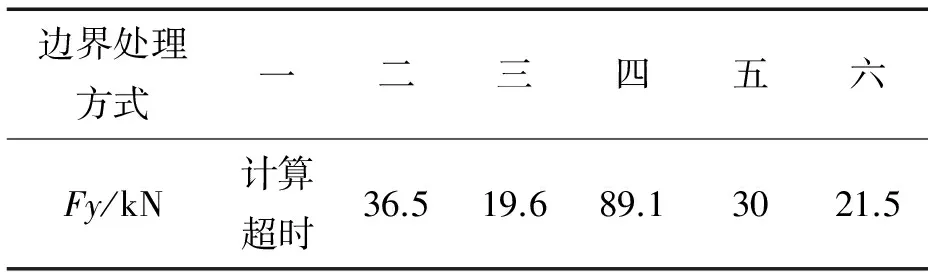
表2
从计算结果可以看出,采用第二种边界处理方式得到的数值计算结果与试验值最为接近。而从实际角度出发,方式一的数值模型最接近真实情况,螺栓与复合材料壳板孔、复合材料壳板与连接钢板、螺栓与连接钢板之间均存在接触关系,但接触问题是一种高度非线性行为,需要较大的计算资源,建立过多的接触会造成时计算时间过长,甚至出现ANSYS无法计算的情况。方式一就是考虑了所有的接触关系,而出现了无法得到结果的情况。
由于复合材料钉孔处所承受载荷主要受与其接触的螺钉影响,故方式二只考虑这一接触关系,其余用耦合重合节点的方式连接,对复合材料壳板与连接钢板只耦合位移主方向Z向的自由度,允许其它方向有相对滑动。螺栓与连接钢板间由于啮合紧密,没有相对位移,故耦合所有方向自由度。该处理方式较接近实际情况,而且计算时间大大减少,其结果也比较接近试验值。
方式三与方式二基本一致,只在耦合自由度上有所不同。将X、Y、Z所有自由度耦合,使所有被耦合节点的X、Y、Z方向位移相同,结构被连成“一体”,忽略了复合材料壳板与连接钢板之间的相对滑动,结果有较大偏差。
方式四不考虑接触关系,全部用耦合方式处理,由于没有建立接触对,使其计算时间非常少,是六种方式里最快的,但其数值计算结果与试验值的误差最大。
方式五、方式六则完全忽略螺栓与连接钢板之间的关系,将其视为一个结构,所不同的是只耦合Z方向自由度,复合材料壳板与连接钢板之间仍可产生相对位移,在载荷方向上位移相同,这与实际情况较一致;耦合X、Y、Z三个方向自由度,将使复合材料壳板与连接钢板“粘”在一起,结构被连成“一体”,导致方式六的结果偏差比方式五更大。
4 结 论
通过数值计算和分析,可以得到以下结论:
1) 采用ANSYS进行复合材料螺栓连接结构仿真计算时,对边界关系的处理方式不仅对计算结果影响较大,而且也会影响计算时间的长短。
2) 当结构存在较多接触关系时,须考虑结构主要受哪些接触关系的影响较大,对主要的接触关系建立接触对,其它的可用耦合节点的方式近似模拟接触关系。本文研究的复合材料螺栓连接结构中,复合材料螺孔与螺栓之间的接触关系为主要连接关系,不能用耦合节点的方式代替,否则会造成计算结果偏差很大;复合材料壳板与连接钢板、螺栓与连接钢板之间的关系对结构的影响较小,可以采用耦合节点的方式近似代替接触。
3) 采用耦合节点方式时需考虑结构之间是否存在相对滑动,在哪些方向上存在相对滑动,耦合具有相同运动趋势方向上的自由度。若忽略结构之间的相对位移关系,耦合X、Y、Z所有方向自由度,会使结构“粘连”在一起,影响计算精度。
4) 本文采用的第二种接触+耦合的边界处理方式不仅能较准确地模拟复合材料螺栓连接结构,而且数值计算时间远小于完全采用接触时的计算时间,大大提高了工作效率。
参考文献:
[1] 沈观林,胡更开.复合材料力学[M].北京:清华大学出版社,2006.
[2] GRUTTA J T, MISKIOGLU I. Strength of bolted joints in composites under concentrated moment[J].Journal of Composite Materials, 2000, 34(15):1242-1262.
[3] CAMANHO P P, MATTHEWS F L. A progressive damage model for mechanically fastened joints in composite laminates[J].Journal of Composite Materials,1999,33(24):2248-2280.
[4] NGUYEN B N. Damage modeling of laminated composites by the use of multilayer volume elements[J].Composites Science and Technology,1998,58(6):891-905.
[5] LIN W H, JEN M H. The strength of bolted and bonded single-lapped composite joints in tension[J].Journal of Composite Materials, 1999,33(7):640-666.
[6] TONG L Y. Bearing failure of composite bolted joints with non-uniform bolt-to-washer clearance[J].Composites Part A, Applied Science and Manufacturing,2000, 31(6):609-615.
[7] MORAIS A B.Open-hole tensile strength of quasi-isotropic laminates[J].Composites Science and Technology,2000,60(10):1997-2004.
[8] GONG X L,GONG X J.Application of tsai-wu criterion to notched and unnothced composite laminates under torque loading[J].Journal of Composite Materials,2000,34(6):460-478.
[9] 边界处理对螺栓连接结构影响的数值模拟研究[C].安世亚太2006年用户年会论文集,2006:1-8.
[10] 王富耻,张朝晖.ANSYS10.0有限元分析理论与工程应用[M].北京:电子工业出版社,2006.
[11] 阚前华,谭长建,张娟,董城. ANSYS高级工程应用实例分析与二次开发[M].北京: 电子工业出版社,2006.
