破损散货船剩余极限强度的评估与分析

1 引 言

在船舶发生碰撞和搁浅事故后，船体的总体强度和局部强度受到了很大的削弱。因此,在救援、拖航中，如果采取的措施不当，可能因为船体剩余强度不够而发生进一步的破坏和更加严重的事故[1]。为了进行救援和防止海洋污染，船体应保持足够水平的剩余强度[2]。由于船体破损属于非常状态，因此应以船体剩余强度来评估其安全性。

近年来，国际船级社协会(IACS)一直在致力于散货船和油船共同结构规范的制定与实施工作。在充分考虑了各方面因素之后，IACS把2006年4月1日作为规范最终生效日期。本文考虑了破损船体在倾斜状态下逐步破坏的力学特性[3]，基于IACS共同规范确定的散货船应力—应变关系，开发编制了散货船结构极限强度的计算程序，用此程序系统计算了某散货船在完整和破损状态下的船体结构极限弯矩，最后得出了一些有应用价值或指导意义的结论。

2 破损船体剩余极限强度评估

2.1 破损模型和剩余极限强度评估指标

船舶在营运中最多见的破损包括碰撞/搁浅两种情况，具体破损状态或程度可通过对过去破损纪录的统计分析来推断其典型破损状态。文献给出了上述两种破损情况下最不利的破损部位和范围，对于散货船情况如图1所示。

图1 散货船碰撞和搁浅后破损部位及程度

破损船体的剩余强度评估指标有两种[4]，一是基于剖面模数的评估指标，一是基于极限强度的评估指标。作者认为对于本文研究的问题，采用后一种评估指标更为合适。这是因为当船舶破损后，一般会出现倾斜漂浮状态，此时如仍采用按甲板或船底的剖面模数已不合适。

基于极限弯曲强度的剩余强度评估指标定义为：

fu=Mu/Mt

(1)

式中：Mu为破损船体的极限弯矩;Mt为破损船体的极端外弯矩。

2.2 破损船体的极端外弯矩

船体结构破损后，由于空舱进水和液体外流，船舶浮态和外载荷分布发生显著变化，其外载荷增加的趋势尤其值得重视。ABS SafeHull给出了破损船体梁总纵弯矩估算公式：

Mt=kusMsw+kuwMw

(2)

式中：Msw,Mw分别是船体梁极值静水和波浪弯矩，可采用IACS[6]公式计算；kus，kuw分别是静水和波浪弯矩的修正系数，取值见表1。

表1 静水和波浪弯矩修正系数

1) 受损船体梁最大静水弯矩的计算公式

中垂：Msw=-0.065C1L2B(0.7+Cb) kN·m

中拱：Msw=0.015C1L2B(8.167-Cb) kN·m

式中：L，B分别为船长和船宽；Cb为船体在夏季载重线处的方型系数；C1为波浪参数：

2) 船体梁波浪诱导弯矩的计算公式

中垂：Mw=-0.11C1L2B(0.7+Cb) kN·m

中拱：Mw=0.19C1L2BCbkN·m

3 逐步破坏分析法的计算流程

船体破损后其剩余有效剖面是非对称的，船体还可能倾斜，如图2所示。图中：OYZ为船体横剖面参考坐标系；C点是形心；CY1Z1是通过形心且与OYZ平行的坐标系；CY0Z0是弹性中和轴坐标系；CYnZn是船体所受弯矩方向坐标系；α是弹性中和轴CY0与船体所受的弯矩方向CYn的夹角；θ是船体的横倾角；E.N.为弹性中和轴；虚线表示船体破损部位。当船体所受弯矩沿Yn轴方向，在坐标系CYnZn中求弹性中和轴时，中和轴的倾角就与船体所受弯矩的大小没有关系，避免了计算斜弯曲的问题。

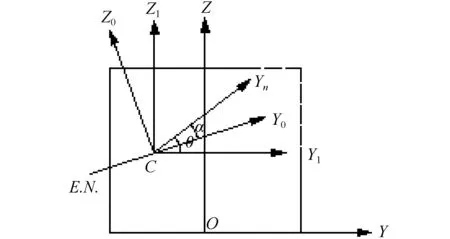
图2 破损船体非对称弯曲的弹性分析坐标系

计算流程可参考文献[6]：

1) 划分单元；

2) 计算CY1Z1坐标系中的几何量Iy1、Iz1、Iy1z1，根据选定的破损船体横倾角来计算CYnZn坐标系中的几何量Iyn、Izn、Iynzn；

3) 根据推导[7]，弹性中和轴CY0与船体所受弯矩方向CYn的夹角α由tgα=Iynzn/Izn确定，从而可以确定初始弹性中和轴，并可计算其对应的始屈弯矩。

4) 确定所有单元的应力—应变关系；

5) 初始化破损船体梁整体曲率，令φ=φ0，认为瞬间弹性中和轴即为有效弹性中和轴，初始曲率φ0由下式确定：

(3)

6) 计算当前每个单元的应变，εi=φ·yi，其中yi是瞬时中和轴到第i个单元的垂直距离，再由单元载荷—端缩曲线σ-ε关系确定当前应变引起的结构单元应力σ；

7) 建立整体截面的力平衡方程以及上下两部分合力作用点的连线F1F2沿着外力矩M的作用平面，更新yi、σi、εi，从而确定当前中和轴的准确位置，计算时需要做一些迭代。中和轴上下平移及转动得满足下式，迭代即完成：

|压力-拉力|/压力≤0.001

|1/kF1F2|≤0.001

(4)

8) 用上部分或下部分的合力P乘以上下两部分合力作用点间的距离F1F2得到当前船体倾角及曲率下船中截面的总弯矩：

M=P·F1F2

(5)

9) 将当前曲率计算的总体弯矩与前一次计算的弯矩比较，判断是否达到极限弯矩值，如果弯矩—曲率曲线斜率为零或为负值，则结束计算，得到极限弯矩Mu，否则返回到第6)步，按初始曲率的10%(φ=φ+0.1φ)逐步增加，重新计算；

10) 改变船体横倾角θ=θ+Δθ，返回第3)步，直到某一横倾角值，算出破损船在各不同横倾角下的剩余极限弯矩。

4 实例计算及结果分析

根据本文提出的方法，对某散货船(源自ISSC2000)在完整状态以及碰撞和搁浅后的船体结构安全性进行评估。图3是该散货船的中横剖面图，其主尺度为：L=285 m,B=50 m,D=26.7 m。散货船在碰撞和搁浅后发生各种不同破损状态下的计算结果见图4～图13。

图3 某大型散货船截面形状与尺寸

以下图中MUH为中拱极限弯矩，MUS为中垂极限弯矩，fuh为中拱剩余强度评估指标，fus为中垂剩余强度评估指标。图4中搁浅是从靠近右舷的船底破损1/6B的范围，图5中碰撞是从船体右舷顶部向下破损1/4D的范围。根据对计算结果的分析，可以得出以下结论：

1) 船在搁浅后，当破损船舶向破损一侧横倾时，剩余强度有所降低。而碰撞后，当破损船舶向非破损一侧横倾时，剩余强度降低，说明此种状态较危险。

图4 搁浅时极限弯矩随船体横倾角的变化曲线

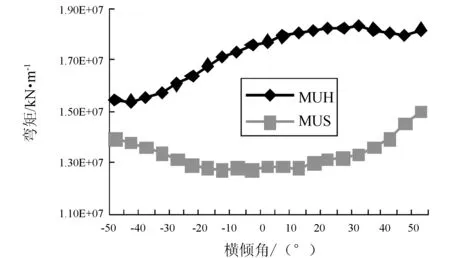
图5 碰撞时极限弯矩随船体横倾角的变化曲线

2) 图6和图7中的B/12、B/8、B/6、B/4分别是从靠近右舷船底的破损范围，图8和图9中的D/7、D/5、D/4、3D/10分别是从船体右舷顶部向下的破损范围。船舶在发生碰撞和搁浅后，剩余极限强度指标随破损范围的增加而下降。不同的是，搁浅时朝破损一侧横倾时下降较多，朝非破损一侧横倾时下降较小；碰撞的情况则相反。

图6 搁浅时fuh在不同破损范围随横倾角的变化曲线

图7 搁浅时fus在不同破损范围随横倾角的变化曲线

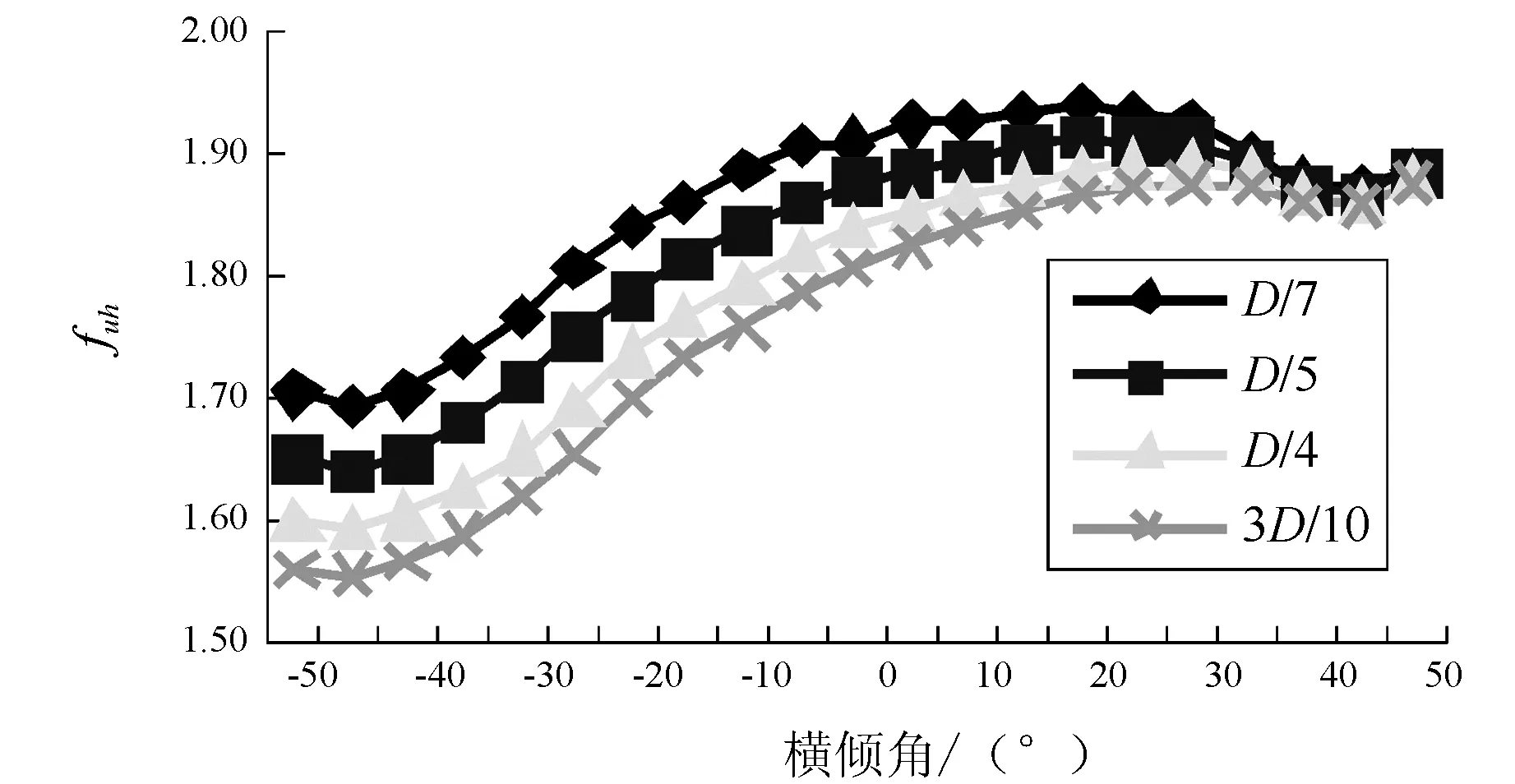
图8 碰撞时fuh在不同破损范围随横倾角的变化曲线

图9 碰撞时fus在不同破损范围随横倾角的变化曲线

3) 图10和图11中的情况一、情况二、情况三分别是从靠近右舷船底开始，以B/6的破损宽度依次向船中移动的三种情况。图12和图13中的情况一、情况二、情况三分别是从船体右舷顶部向下，以D/4的破损高度向中和轴移动的三种情况。船体搁浅后，剩余极限强度指标随破损位置的不同变化不大。船舶发生碰撞后，破损位置离中和轴越远，剩余极限强度将越小。

图10 搁浅时fuh在不同位置处随横倾角的变化曲线

图11 搁浅时fus在不同位置处随横倾角的变化曲线

图12 碰撞时fuh在不同位置处随横倾角的变化曲线

图13 碰撞时fuh在不同位置处随横倾角的变化曲线

5 结 论

本文给出的计算破损船体非对称极限弯矩的和计算程序，既可以考虑剖面的非对称性，还可以考虑船体横倾的影响。通过对船体在不同破损状态下剩余极限强度的分析，得到了有应用价值或有指导意义的计算结果和结论，对船舶安全性和规范、法规的制定，以及船舶在碰撞和搁浅后救援、拖航中剩余极限强度评估具有一定的参考价值。

参考文献:

[1] OHTSUBO H, et al. Structural design against collision and grounding[C].Proceedings of 13th International Ship and Offshore Structures Congress, 1997.

[2] 祁恩荣, 崔维成. 船舶碰撞和搁浅后剩余强度可靠性评估[J]. 船舶力学,1999,3(5):40-46.

[3] 何福志,马建军,万正权.船体结构总纵极限强度的简化逐步破坏分析方法[J].中国造船,2005,46(2):17-27.

[4] 杨平.船体结构极限强度及破损剩余强度的研究[D].武汉:武汉理工大学, 2005.

[5] NITTA A, ARIA H, MAGAINO A. Basic of IACS unified longitudinal strength standard[J]. Marine Structures, 1992,5(1):1-21.

[6] 刘俊梅.船体极限强度及受损船体剩余极限强度分析[D].武汉理工大学，2005.

[7] 刘鸿文，材料力学[M].北京：高等教育出版社，1991.