罗经回路在船用航姿系统中的应用与工程实现
2008-04-24孟祥涛,蔡春龙
1 引 言
捷联式航姿系统是一种低成本、自主式的航向姿态基准系统,在军事上作用明显,现在已经逐渐应用到舰船领域,它主要用于实时测量并输出载体的航向信息和两个水平姿态信息。目前,虽然捷联惯导系统(SINS)与GPS全球定位系统具有完美的互补特性,可实现满意的性价比,但因GPS信号易受干扰且受制于人,难以在战时发挥效能[1,2]。所以,如何利用惯性航姿系统自身的信息来提高航姿精度便成为当前研究的热点。
无阻尼航姿系统是一临界稳定系统,系统的误差是周期振荡的,而且幅值是不衰减的[3,4]。这对于工作时间较长的航姿系统来说是不能满足使用精度要求的。为了提高航姿系统长时间工作的精度性能,本文将惯性平台系统精对准的思想引入到捷联航姿系统中,将水平姿态角误差的舒勒周期振荡抑制下来,傅科周期振荡就自然消失[5-8],同时利用罗经回路使航向角误差的地球周期振荡消失,幅值得到衰减,这样就可提高航姿精度[9,10]。在此基础上提出了对原有捷联航姿算法的修改方法,并通过数字仿真验证了此方法是可行的,在工程上是能够实现的。
2 内全阻尼网络的设计
2.1 水平阻尼网络的设计
舰船在系泊状态下,忽略速度误差中因补偿有害加速度而引起的交叉耦合项,无阻尼惯导系统的误差可以简化为如下形式:
(1)
式中,ΔAx、ΔAy为加速度计的零位偏置;εx、εy、εz为陀螺的漂移。进一步忽略φx、φy之间的交叉耦合项后,可得到两个独立的水平误差方程:
(2)
两个水平通道是相似的,区别仅在于东向轴修正回路中有方位误差项,而北向轴修正回路没有此误差项,下面就以东向轴为例来讨论阻尼网络的设计问题。

(3)
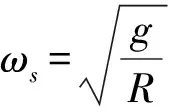
s1=-σ,s2,3=-σ±jωd
合理地选择σ和ωd,便可以将特征方程的根配置在复平面的左半平面,从而确定参数K1,K2,K3。
2.2 方位罗经回路的设计
由系统误差方程可知,方位误差角会引起平台坐标系(数学平台)绕东向轴的水平误差角,这将使加速度计的北向投影敏感到重力加速度的分量,从而导致北向速度产生误差,这就是我们通常所称的“罗经效应”。由此可见,δνy是“罗经效应”项 -ωiecosφ·φz的一种表现。如果我们用δνy来控制方位误差角φz,而φz又影响水平误差角φx,φx又决定北向加速度计的输出,经过积分影响到了δνy,这样就形成了罗经回路,如图2所示,它可以用于阻尼方位误差角的发散。

图2 罗经回路结构图
由图2可得到罗经回路的特征方程为:
南京地铁于2010年前后提出了“全效修”维修集约范式表述。该范式可视为“均衡修”维修集约范式的一类演变形式。
+gωiecosφ·K(s)=0
(4)
将K(s)设计成下面的形式:
(5)
这样特征方程变成:
(6)
在设计时可使特征方程具有两重根:

3 阻尼网络参数的设计
在水平回路中,为了简便起见,我们选择3个相等的负实根作为特征方程的解,从调节时间、超调量和稳态误差3个方面综合考虑,令特征方程的根为:
在方位回路中,用罗经回路的特征方程来求取相关的参数,但是由于缺少与K3有关的积分项,故上述参数不适合东向轴的水平回路,但是适合北向轴的水平回路,东向轴和方位轴由罗经回路来确定参数,罗经回路的特征方程可以表示为:
(7)
根据上式,ξ、ωn与特征方程根的参数σ′、ωd的关系为:
(8)
此时系统的特征方程用σ′、ξ表示为:
(9)
设计时令K1=K4,则有:
(10)
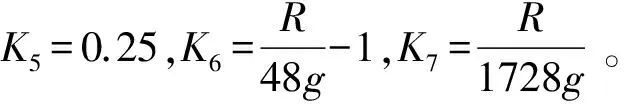
4 全阻尼惯导的基本方程
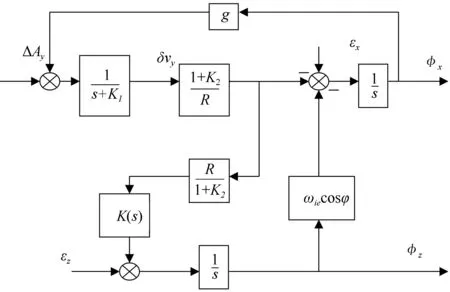
图3 罗经回路等效方框图
设北向轴、东向轴水平回路的阻尼网络分别为Hx(s)、Hy(s),由上述分析可以得到:
(11)
解得:
(12)
方位阻尼网络:
(13)
则数学平台的控制指令角速度在导航系下的投影为:
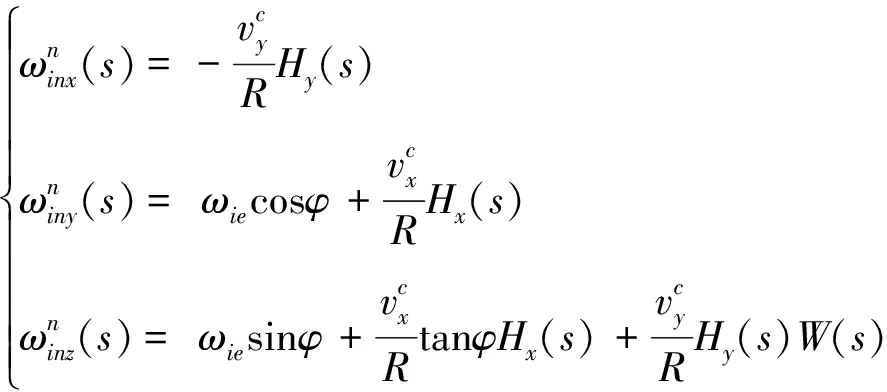
(14)
由于载体的速度在一个采样周期内变化很小,我们可以认为是一个常量,同理纬度也认为是常量,则上述的控制指令角速度的时域表达式可以写成:
(15)
由于K1=K4,将指数用多项式展开,其中T为采样周期:
(16)
5 仿真研究
为了验证以上推导的算法的正确性和基于全阻尼航姿算法的效果,作者按照上面的基于内全阻尼的航姿算法编制了相关程序并进行了仿真研究,分别在静基座和系泊状态下仿真,选定系统参数为:K1=0.008 26;K2=33.78;K3=7.266 4×
舰船在系泊状态下状态参数为:纵摇角θ=10°sin 0.0025t;横摇角γ=20°sin 0.0015t;航向角ψ=15° sin 0.0024t。
设定IMU的精度为:三轴陀螺的常值漂移为0.1 °/h,三轴加速度计零偏均为10-4g,仿真时间为100 min,结果如图4、图5所示,图4是在静止条件下的航姿误差曲线,图5是载体在系泊状态下的航姿误差曲线,其中虚线为无阻尼系统的航姿误差曲线,实线为内全阻尼系统的航姿误差曲线。

图4 航姿误差曲线

图5 系泊状态航姿误差曲线
由仿真结果可以看出:用内全阻尼网络设计航姿系统时,可以使载体在静态下的航姿精度得到明显的提高,纵摇角的精度提高了3倍,横摇角的精度提高了2倍,最为明显的是航向角的精度提高了近一个数量级,并且没有发散的趋势,而航向角精度一直是我们努力争取改善的性能指标,经过内全阻尼后,航向角精度高于水平姿态角的精度,使整体性能大大改善。
6 结 论
本文从工程实用的角度出发,将平台精对准中的罗经回路思想引入到捷联航姿系统中,形成了内全阻尼网络,研究了参数的设计方法,改进了原有的数学平台控制指令角速度方程,仿真结果表明新的算法提高了航姿精度,尤其抑制了航向角误差的发散。
新的航姿算法不需要利用外界的任何信息,用自己的速度来修正姿态,实现了完全自主导航的目的,但是,全内阻尼算法改变了原有的舒勒调谐回路,无法隔离载体运动对航姿误差的影响,所以当载体做大机动运动时,应该切换到纯惯导无阻尼状态进行导航。
参考文献:
[1] DU Ya-ling,LIU Jian-ye,LIU Rui-hua,ZHU Yan-hua.The fuzzy kalman filter of damp attitude algorithm[J].Journal of Astronautics,2007,28(2):305-309.
[2] 杜亚玲,刘建业,刘瑞华,孙永荣.捷联惯性航姿系统中的模糊内阻尼算法研究[J].南京航空航天大学学报,2005,37(3):274-278.
[3] 陈永冰,钟斌.惯性导航原理[M].北京:国防工业出版社,2007.
[4] VANDERWERF K. Schuler pumping of inertial velocity errors due to gravity anomalies along a popular North Pacific airway[C]//Position Location and Navigation Symposium,IEEE,1996:642-648.
[5] 刘建业,杜亚玲,祝燕华,李荣冰.航姿系统内阻尼的模糊自适应滤波算法[J].南京航空航天大学学报,2007,39(2):137-142.
[6] 高亚楠,陈家斌,杨亭鹏.捷联式光纤陀螺罗经系统误差分析[J].北京理工大学学报,2005,25(5):423-426.
[7] 刘为任,庄良杰.惯性导航系统水平阻尼网络的自适应控制[J].天津大学学报:自然科学与工程技术版,2005,38(2):146-149.
[8] 赵汪洋,杨功流,庄良杰.双惯导系统水平阻尼技术研究[J].系统仿真学报,2007,19(5):1109-1111.
[9] BENSON D O. A comparison of two approaches to pure-inertial and doppler-inertial error analysis[J].IEEE Transaction on Aerospace and Electronic Systems(SO18-9251),1975,11(3):447-455.
[10] 祝燕华,刘建业,曾庆化.基于故障检测的惯性航姿系统内阻尼姿态组合算法[J].应用科学学报,2007,25(2):183-188.
