近水面水下爆炸作用下舰船损伤数值模拟

， ，

(1.连云港市91316部队， 江苏 连云港 222046； 2.海军工程大学 船舶与动力学院，武汉 430033)

舰船承受水下爆炸载荷是舰船结构在很短的时间内,在巨大冲击载荷作用下的一种复杂的非线性动态响应过程,属大变形、强非线性问题[1]。同时还涉及到水下爆炸载荷和舰船结构的相互耦合作用。由于水下爆炸的复杂性,对其进行详细的理论研究,并通过建立精确的数学模型,使水下爆炸问题得到完全的解析是十分困难的，主要是通过实验提出一些经验公式[2-3]。而爆炸实验属于破坏性实验,实验经费昂贵、实验设备复杂,不能从根本上解决这一问题。近几年计算机技术的飞速发展使得舰船在水下爆炸载荷作用下的数值模拟成为可能[4]，MSC/DYTRAN具有丰富的材料模式、动态方程以及各种起爆条件,能够模拟爆炸波的传播和爆轰产物的运动,以及结构对爆炸冲击波的响应[5]。因此，考虑针对某型水面舰船舭部舱段缩比模型采用大型通用有限元程序MSC/DYTRAN，对结构在水中爆炸冲击波载荷作用下的动态响应进行了数值模拟和分析。

1 数值模拟方法

1.1 欧拉流体的参数设置

采用一般耦合法计算，为了保证计算精度，增加炸药中心的网格密度，以期精确模拟炸药爆炸情况。在炸药半径小于网格密度时，可以通过增加状态方程的参数来模拟水下爆炸压力场[5]，但是这种方法当炸药药量或流体区域改变时，不能保证调整好的压力场和炸药质量是正确的，必须再进行调整。关于炸药量的计算，当球形炸药没有全部包含在流体网格内时，本文通过计算发现MSC/DYTRAN只计算流体网格中的炸药量。

本文采用调整网格密度的方法进行水下爆炸的数值模拟，见图1。

图1 流体边界设置和网格划分示意

炸药放置在O处时，质量是200 g，半径为0.048 9 m，爆炸点附近的网格密度是0.02 m，远离爆炸点的网格密度是0.08 m。ABFG面、DEFG面和BCEF面设为流出边界，其余各面设为对称面。计算时还发现，可以将空气的比内能设置为0，这样做就可以避免由于水和空气的初始压力设置的不同，空气压力向水中传播的情况。在有空气和水共存的流体区域中，空气的比内能设置为0，还可以将时间步长增加，从而加快了计算速度，而且对计算结果并无影响。

1.2 爆炸场的DYTRAN数值解

库尔的关于冲击波峰值压力和比冲量的经验公式各个单元的计算位置见图2所示。

图2 单元模型计算位置示意

由DYTRAN软件所计算出的一个单元的压力时程曲线见图3。各个单元所在的峰值压力见表1。

表1经验值和DYTRAN数值解比较

单元编号距离/m经验值/MPaDYTRAN值/MPa单元编号距离/m经验值/MPaDYTRAN值/MPa336140.11345322345801.052620.4337610.20175184347271.2822.014.9338870.29115101349581.741510.3340550.4374.071.2351682.26117.45342650.644641.8359242.6195.36

图3 单元33761压力时程曲

由表1数值可以看出，当单元与爆炸中心的距离是0.11 m时，DYTRAN计算值近似等于经验值，此处不受结构及水面效应的影响；当单元与爆炸中心的距离是0.64 m时，单元的压力时程曲线不再是单一的指数形式，而是出现了好多的小脉动，但此时结构及水面效应的影响还是可以忽略的；随着单元与爆炸中心距离的增大，DYTRAN计算值与经验值的偏差也越大，结构及水面效应对峰值压力的影响也越来越明显。从经验值和DYTRAN数值解随距离变化曲线(图4)可以看出，使用本文中的数值模拟方法模拟近水面炸药爆炸场是合理可行的。

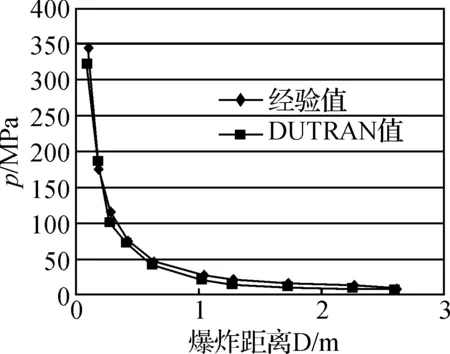
图4 经验值和DYTRAN数值解随距离变化曲线

2 舭部舱段损伤数值计算

2.1 计算工况

舷侧舭部板架有限元模型结构见图5、6，该模型设计目的在于考核舷侧舭部舱段之间的板架在水下爆炸作用下的损伤。外板为一圆弧，厚1 mm，其上有肋骨支撑。甲板、纵向舱壁和外底厚1 mm，横梁和纵向舱壁肋骨为T型钢。中间舱段长600 mm，两端舱段各长300 mm。横向舱壁板厚1 mm。

模型材料为低碳钢，计算中采用双线性强化模型，弹性模量为210 GPa, 泊松比为0.3，密度为7 800 kg/m3，强化模量为250 MPa，静态屈服极限为250 MPa。材料在强冲击载荷作用下，一般会产生比较明显的应变率强化效应，特别是对于低碳钢这种应变率敏感材料。本文计算中应变率强化模型采用Cowper-Symonds模型。

图5 舱段模型

图6 舱段模型剖面示意

文章对7种工况进行计算，见表2。

表2 不同工况

装药在同一沉没深度装药爆距的变化对水下爆炸的影响，在装药沉没深度为0.96 m的情况下，爆距分别为1.5、1.6、1.8和2.0 m。在装药爆距1.5 m不变的情况下，攻角分别为30、45、60和75°，相应的装药沉没深度分别为0.96、1.34、1.65和1.82 m，考察装药沉没深度变化对水下爆炸的影响。爆炸环境见图7。压力历时曲线是距离炸药中心1.5 m处舱段模型上的点的压力变化曲线。

图7 Dytran计算工况示意

2.2 装药沉没深度对水下爆炸的影响

当装药沉没深度为0.96 m时，模型最大变形值是1.22 cm，测点的最大压力值为30 MPa，这与试验结果相符合。当装药沉没深度为1.34 m 时，模型最大变形值是1.62 cm，测点的最大压力值为37.5 MPa；当装药沉没深度为1.65 m 时，模型最大变形值是1.71 cm，测点的最大压力值为38.8 MPa；当装药沉没深度为1.82 m 时，模型最大变形值是2.00 cm，测点的最大压力值为41.5 MPa。

由以上计算结果可以看出，最大压力值是自由场压力值的2～3倍，随着装药沉没深度的增加，模型的最大变形与最大压力值是不断增加的；当攻角由30°变化到45°时，模型的最大变形与最大压力值有显著增长；当攻角由45°变化到60°时，模型的最大变形与最大压力值变化不是很明显；当攻角由60°变化到75°时，模型的最大变形与最大压力值增加很小，最大变形与最大压力值在此深度后将逐渐趋于稳定。从模型最大变形和炸药沉没深度的拟合曲线图9可以看出，当装药沉没深度逐渐增加时，变形并不是线性增加，而是出现了2个较清楚地拐点。

图8攻角为30°变形云图和壁压历时曲线

图9 模型最大变形随着装药沉没深度变化曲线

图10 模型最大变形随着爆炸距离变化曲

2.3 装药爆距对水下爆炸的影响

当装药爆距为1.6 m时，模型最大变形值是1.07 cm，测点的最大压力值为28.1 MPa；当装药爆距为1.8 m时，模型最大变形值是0.97 cm，测点的最大压力值为26.2 MPa；当装药爆距为2.0 m时，模型最大变形值是0.67 cm，测点的最大压力值为21.4 MPa。

由以上计算结果可以看出，随着装药爆距的增加，最大变形与最大压力值下降很快，由1.5 m变化到2.0 m时，最大变形值下降了50%，最大压力值下降了30%。可以看出，当装药爆距继续增大时，最大变形与最大压力值还将继续下降，最大变形和最大压力值将随着距离的增加逐渐趋于0。从模型最大变形和爆炸距离的拟合曲线图可以看出，当爆炸距离逐渐增加时，最大变形并不是线性下降，而是出现了两个较清楚地拐点，而且随着距离的增加，最大变形下降很快。

图11爆距为1.6m壁压历时曲线

3 结论

1) 从欧拉流体区域参数设置着手,将数值方法计算结果与库尔经验值比较,得出使用该方法研究近水面水下爆炸冲击波问题是可行的。

2) 当舰船受到近水面的炸药冲击波袭击时，其损伤效果与远场水下爆炸不同的是与炸药中心和舰船的相对位置有关。当装药沉没深度越深时，舰船受到的损伤越大,但是在这过程中出现了2个拐点；当炸药中心与船体距离越近时，舰船受到得应力越大,在变化过程中也出现了两个拐点。但是由于水面效应的影响，当炸药中心与船体距离变近时，舰船受到得应力也可能变大。

3) 将来可以利用MSC/DYTRAN软件进行后续计算，讨论近水面水下爆炸时，同等药量下，炸药对舰船的最佳攻击角度；不同药量下，炸药对舰船的最佳攻击角度的变化。

[1] 罗松林,叶序双,顾文彬,等.水下爆炸研究现状[J].工程爆破,1999,5(1):83-84.

[2] 库尔P.水下爆炸[M].北京:国防工业出版社,1960.

[3] Olson M D,Nurick G N, Fagnan J.R.Deformation and rupture of blast loaded square plates-predictions and experiment[J].Int J Impact Engng,1993,13(2):279-291.

[4] 符 松,王智平,张兆顺,等.近水面水下爆炸的数值研究[J].力学学报,1995,27(3):267-276.

[5] 张振华，朱 锡，白雪飞．水下爆炸冲击波的数值模拟研究[J].爆炸与冲击, 2004(2)：87-92.