高速单体船推进系统参数辨识方法研究

， ， ，

(江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)

与船舶推进运动相关的参数分为两大部分，最为重要的是螺旋桨的一系列参数，其次是伴流分数和推力减额。现阶段实船大多数选用系列桨，即在选定好桨的同时已经能通过查图谱得到该桨型的敞水性能曲线。但是在加工螺旋桨时因施工影响，大部分桨型与其所对应的理想桨型存在着一定的误差，这就造成了敞水性能与图谱有差别。

由于船舶航行时工况的不稳定以及船尾螺旋桨的空泡效应使得船舶实际的螺旋桨敞水性能和理论值有比较明显的误差。

考虑船舶运行数年后型线发生变化以及海况的影响，船舶在运行过程中的船身效率和相对旋转效率都是不确定的。因此通过测得船舶在运行时的速度和主机功率来辨识出船舶推进系统的各参数是比较有意义的。

现阶段系统辨识在船舶运动模式上的应用主要是集中在船舶的操纵性运动模式上。[1-2]本文将系统辨识应用到船舶推进系统中，通过仿真得到输入和输出量辨识出推进系统中的各待辨识参数包括伴流分数，推力减额以及螺旋桨的一系列水动力参数。在辨识的算法选择中用遗传算法的优化方法作为辨识方法。

1 数学模型

1.1 高速单体船的阻力

先期工作已经完成，基于MatLab的Simulink工具箱编写高速单体船推进系统的仿真实验平台[3]。利用该平台，可以在不通过实船与模型试验的情况下，得到有关的数据参量，为试验数据处理辨识方法研究提供便利。

利用该仿真平台，读取高速单体船在某一航速下的主机功率的值。利用下式可以得到船舶航行的阻力R。

(1)

式中：Pe——有效功率；

Ps——轴功率；

ηs——轴传送效率，取0.98；

ηr——相对旋转效率；

ηh——船身效率；

ηo——螺旋桨敞水效率。

对给定的螺旋桨而言，推力系数、转矩系数和敞水效率仅与进速系数有关，因此有：

(2)

(3)

式中：kt——推力系数；

kq——转矩系数；

T——螺旋桨推力；

Q——螺旋桨转矩；

J——进速系数；

t——推力减额；

W——伴流分数。

将式(2)和(3)代入式(1)并整理得：

(4)

即将阻力化作关于kq,kt,ηr的函数。

1.2 高速单体船推进系统

在船舶的推力系统中主要的物理量有

推力T，转矩Q，敞水效率ηo，有效推力Tp进速Va，进速系数J。

由于在很多情况下，可以将kt-J以及10kq-J的关系曲线看作是两个二次函数的拟合[2]。即：

kt=a0J2+a1J+a2

(5)

10kq=b0J2+b1J+b2

(6)

可见在螺旋桨确定后kt-J和10kq-J都是确定的，即式(5)、(6)中的ai,bi(i=0,1,2)都是定值。

1.3 数学模型

为进行推进系数的辨识，选取船舶在匀加速直线的状态作为研究对象，根据平动方程有：

zp(1-t)T-R=1.1△a

(7)

式中：a——加速度,常数；

△——排水量，常数。

将式(7)中各量分解

(8)

式中：zp为螺旋桨个数。

将上kt各式带入式(8)，测取一系列的航速时的数值，令：

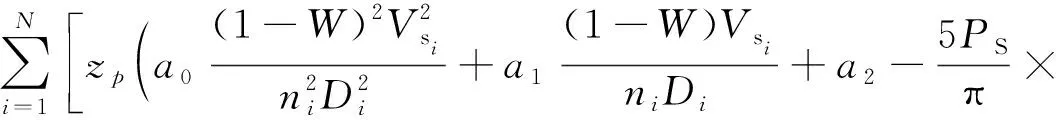
(9)

辨识模型中输入量有：n,Vs,Ps,D,△,a,zp；输出量即辨识参量为：ai,bi,W,t,ηr(i=0,1,2)。

2 辨识方法

由于在辨识的过程中其各待辨识参数都是常量，即与时间无关，采取离线辨识即可。笔者在辨识中采用优化的方法，通过给出各设计变量的范围选用适合的优化方法得到需要辨识的各参数。优化的三要素为设计变量、目标函数和约束条件。

2.1 设计变量

选用上面9个输出量作为设计变量：表示kt-J和10kq-J曲线的6个系数a0、a1、a2、b0、b1、b2还有ηr，W和t。

将这9个设计变量用一个向量X来表示：

XT={a0,a1,a2,b0,b1,b2,W,t,ηr}

2.2 目标函数

通过仿真平台，取得在一系列的进速系数下船舶在稳定前进时的Vs、a、n、Ps，分别记此时的数据为Vsi、ai、ni、Psi，则优化目标函数的表达式为(9)。

2.3 约束条件

对这个目标函数的优化约束条件主要为转矩的等式约束和设计变量上下限的约束。

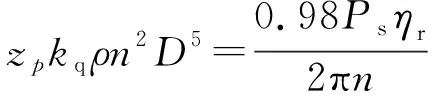
(10)

包括a0,a1,a2,b0,b1,b2,(1-W),(1-t)

一般取： 0.05≤W≤0.4；

0.05≤t≤0.15；

0.9≤ηr≤1.1。

根据二次曲线的意义一般取：

-0.50≤a0≤-0.05；

-0.50≤a1≤-0.05；

0.30≤a2≤0.80；

-0.50≤b0≤-0.05；

-0.50≤b1≤-0.05；

0.30≤b2≤1.5。

2.4 优化方法

在辨识此系统的各系统参数的过程中，由于遗传算法[4-5]作为优化算法在全局优化上有着比较明显的优势而且原理较为简单比较容易实现，因此选用遗传算法作为优化方法。

在VC++界面中编写适应度函数和主程序。编写主程序时将各个设计变量的上下限，选择方法，种群数，遗传的代数等确定。

基因：x1,x2,x3,x4,x5,x6,x7,x8,x9对应优化数学模型中的a0,a1,a2,b0,b1,b2,W,t,ηr；

染色体：{x1,x2,x3,x4.x5,x6,x7,x8,x9}的二进制编码的字符串，即对应于设计变量的组合；

种群数：这里的设计变量有限，选择种群数500。实际效果被证明很好。

遗传代数：选择3 000代。

2.5 惩罚策略

将约束条件加入到目标函数当中，根据经验惩罚因子[5-6]取10。并在适应值函数中选用乘法的形式作为惩罚项。

3 算例以及分析

本论文选用1 000 t的高速单体船在20个稳定航速变化下的仿真模型作为研究的对象，分别在Simulink下读取各参量的值，再利用遗传算法对该模型进行系统辨识，从而用辨识出的kt-J曲线和10kq-J与仿真模型下的各点做比较。

其中高速单体船的五叶螺旋桨P/D=0.85，Ae/Ao=0.6，遗传算法中选种群为500，代数为3 000代，交叉率为0.8,变异率为0.05。可以得到最大的适应值函数的值为-0.009 677，其中各代辨识参数值为：

a0=-0.153 3，a1=-0.275 5，a2=0.401 3，

b0=-0.214 9，b1=-0.250 6，b2=0.496 1，

W=0.065 3，t=0.081 9，ηr=0.978 2

根据上面的数据用二次拟合出的曲线见图1。

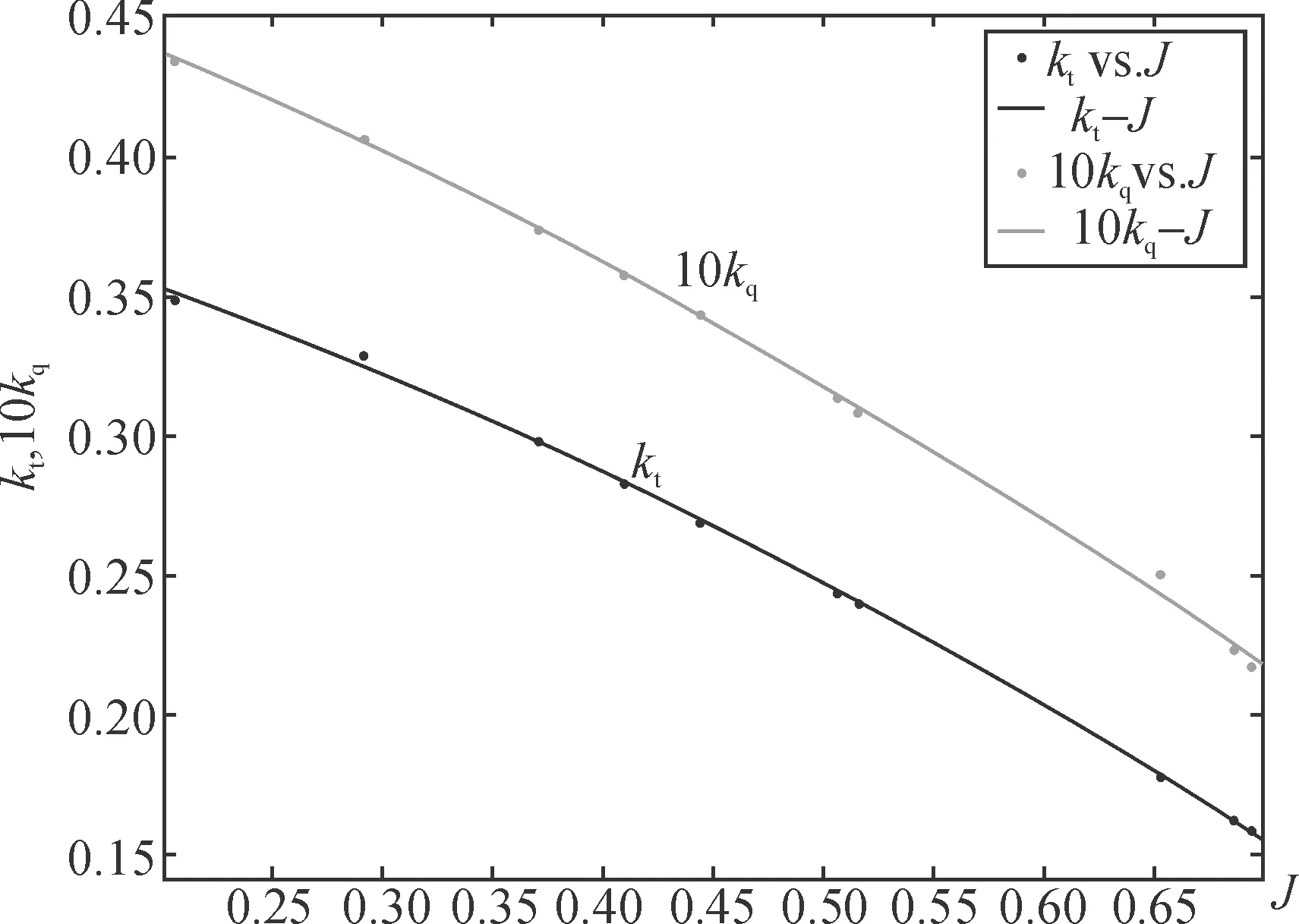
图1 螺旋桨推力系数和转矩系数曲

从上面的图中，可以看出由二次函数拟合出的kt-J和10kq-J的曲线可以比较近似的反映出螺旋桨推进系数和进速系数的关系。图中的10个点分别是用仿真的方法取得的J在0.2～0.8范围内时kt和10kq的数值。

除了有些点有明显误差外其余的点吻合都不错。可以看出如果在能取得足够多航行实验的情况下可以做到拟合出的kt-J和10kq-J曲线能够满足设计者的要求。由此证明了该方法用于高速单体船推进系数的辨识是可行的。

[1] 乐美龙.船舶操纵性预报与港航操纵运动仿真[M].上海：上海交通大学出版社, 2004.

[2] 贾欣乐, 杨盐生.船舶运动数学模型机理建模与辨识建模[M].大连：大连海事大学出版社, 1999.

[3] 王 义, 董 亮, 杨松林.基于在线仿真的穿浪船推进智能控制及系统优化研究[J].江苏科技大学学报：自然科学版, 2006,20(1):11-15.

[4] 玄光男, 程润伟.遗传算法与工程设计[M].北京：科学出版社, 2000.

[5] 米凯利维茨 Z.演化程序——遗传算法与数据编码的结合[M].北京：科学出版社, 2000.

[6] 张火明, 杨松林.遗传算法在船舶航行性能优化中的惩罚策略[J].华东船舶工业学院学报：自然科学版, 2001,15(4):1-5.