面元法预估导管螺旋桨定常性能的一种简便方法
2007-01-28
海军工程大学 船舶与动力学院 武汉 430033
导管螺旋桨通过改变螺旋桨桨叶盘面处的来流使螺旋桨获得较高的效率,被广泛应用于大型、高负荷的船舶。但是,导管和螺旋桨的相互关系如果处理不好往往会降低推进系统效率,严重的还会产生导管振动和空泡剥蚀、噪声等问题,因此,从理论上预报导管螺旋桨的水动力性能十分重要。
势流范围内的导管螺旋桨定常性能预估已有大量研究。比较成熟的是迭代求解法[2-5],即应用涡格法+面元法[2-4]或面元法+面元法[5,6]分别计算桨和导管的性能,再利用迭代方法使结果达到收敛。
该方法在计算中分别计算桨对导管以及导管对桨的诱导速度,迭代过程花费较多时间,因此,建立一个基于速度势的面元法+面元法求解均流中导管螺旋桨定常性能的较为简便的方法。
1 数值方法
1.1 离散化
考虑导管桨在无限大的均匀来流中工作的情况,假设为理想流体,不可压缩。建立图1所示直角坐标系o-xyz,x轴与桨轴线重合并以下游为正方向,y轴以垂直向上为正方向,z轴按右手法则确定。桨工作时,导管和桨以VA沿x轴负方向运动,桨叶旋转速度为Ω。

图1 导管螺旋桨坐标
应用面元法对导管和螺旋桨求解,计算过程中将桨、导管和桨毂看作一体。螺旋桨、导管和桨毂表面采用四边形双曲面元进行离散。对于定常问题,每个桨叶及它泄出的尾涡片所处的情况是相同的。设共有Z个桨叶。如果把桨毂表面周向分成Z个区间,则各区间相互之间亦处于相同情况。因此,只要解决一个叶片及与它连带的一个桨毂表面区和一个尾流区,那么整个问题就可以解决了。螺旋桨桨叶表面离散为MP×2NPD个面元,其中MP和NPD为径向和弦向面元数,螺旋桨一个桨叶对应的导管表面离散为NCD×2NXD个面元,其中NCD和NXD分别为周向和轴向面元数,相邻桨叶间桨毂表面离散为MNW个面元,导管桨单个桨叶对应部分表面总的离散面元为:MPRD=MP×2NPD+NCD×2NXD+MNW导管桨的离散网格如图2所示。

图2 导管螺旋桨离散网格
螺旋桨和导管的尾涡采用近似模型。螺旋桨尾涡面具有收缩和螺距变化,导管尾涡面具有收缩,至下游某一指定位置后保持常量至远下游,桨尾涡面离散为MP×NW个四边形双曲面元,导管尾涡面离散为NCD×NDW个四边形双曲面元。螺旋桨和导管的尾涡离散网格见图3、4。
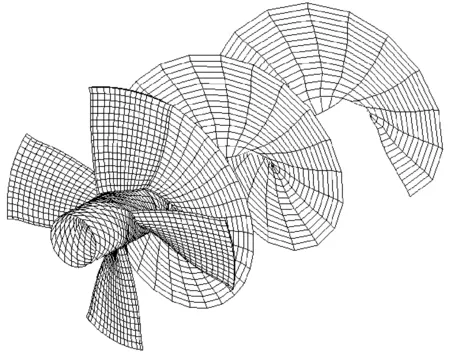
图3 螺旋桨尾涡离散网格图

图4 导管及其尾涡离散网格
桨和导管表面各离散单元均布偶极子和源汇,尾涡面上均布偶极子,各单元的形心为控制点。这样可以把整个桨表面扰动速度势方程离散为
(1)
式中:N——单个桨叶以及及叶对应的桨毂和导管表面总的控制点数;
MP——单个桨叶尾涡条带数;
NCD——单个桨叶对应导管部分尾涡条带数;
Aij、Wik、Wil、Bij——影响系数。
对于近场,影响系数可通过解析方法积分求得精确解,对于远场,可通过高斯积分求得近似解。
通过求解线性方程组(1),可得到导管螺旋桨表面扰动速度势的值。
1.2 库塔条件
对桨叶随边处和导管分别应用等压库塔条件,即要求桨叶临近随边上下面元和导管临近尾端处上下表面的控制点处有相等的压力。桨叶和导管的库塔条件如下式:
(2)
Δpk=pU-pL=0k=1,2,…,NCD
(3)
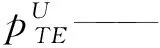

pU——导管临近尾端内侧面元所受压力;
pL——导管临近尾端外侧面元所受压力。
分别采用Newton-Raphson迭代方法进行迭代求解,求解时ΔΦ的初值取Morino线性库塔条件的值。
1.3 桨的推力和转矩
螺旋桨和导管的推力和转矩可通过求解桨叶桨毂和导管表面的压力分布并计及粘性阻力分量来得到。由压力分布积分可得到推力和转矩的公式:
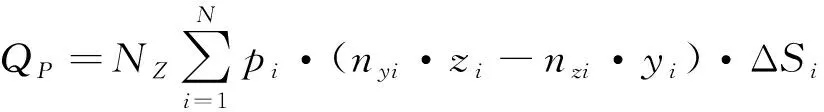
式中:pi——物面上某面元形心处的压力。
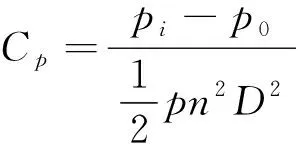
桨叶的粘性阻力计算如下,CD取0.004 5。

|vi|·ΔSi
2 数值计算结果
应用本方法对简易导管桨系列进行了计算,改系列桨包括JD7704+Ka系列和JD75+Ka系列两组桨,导管和螺旋桨的几何参数和实验数据见文献[6]。计算中每个桨叶弦向和展向面元数取为16×16,为均匀划分,导管周向和弦向面元数取为40×36,为均匀划分。
图5~9是利用本方法计算结果与试验结果[6]的比较。
可以看出,在较大的进速系数范围内总推力和转矩的计算结果与实验结果吻合较好,导管推力在桨工作状态左右与试验结果吻合较好,但在载荷较重时计算结果偏低。
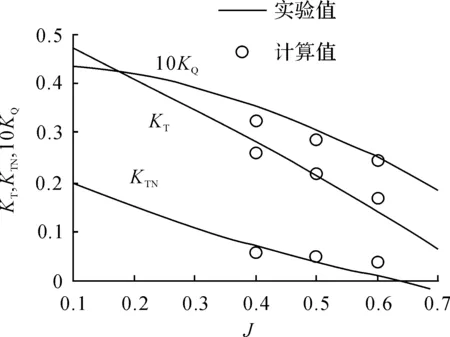
图5 JD7704导管+Ka4-70(P/D=1.0)桨敞水性能比较

图6 JD7704导管+Ka4-55(P/D=1.0)桨敞水性能比较

图7 JD7704导管+Ka4-70(P/D=0.8)桨敞水性能比较
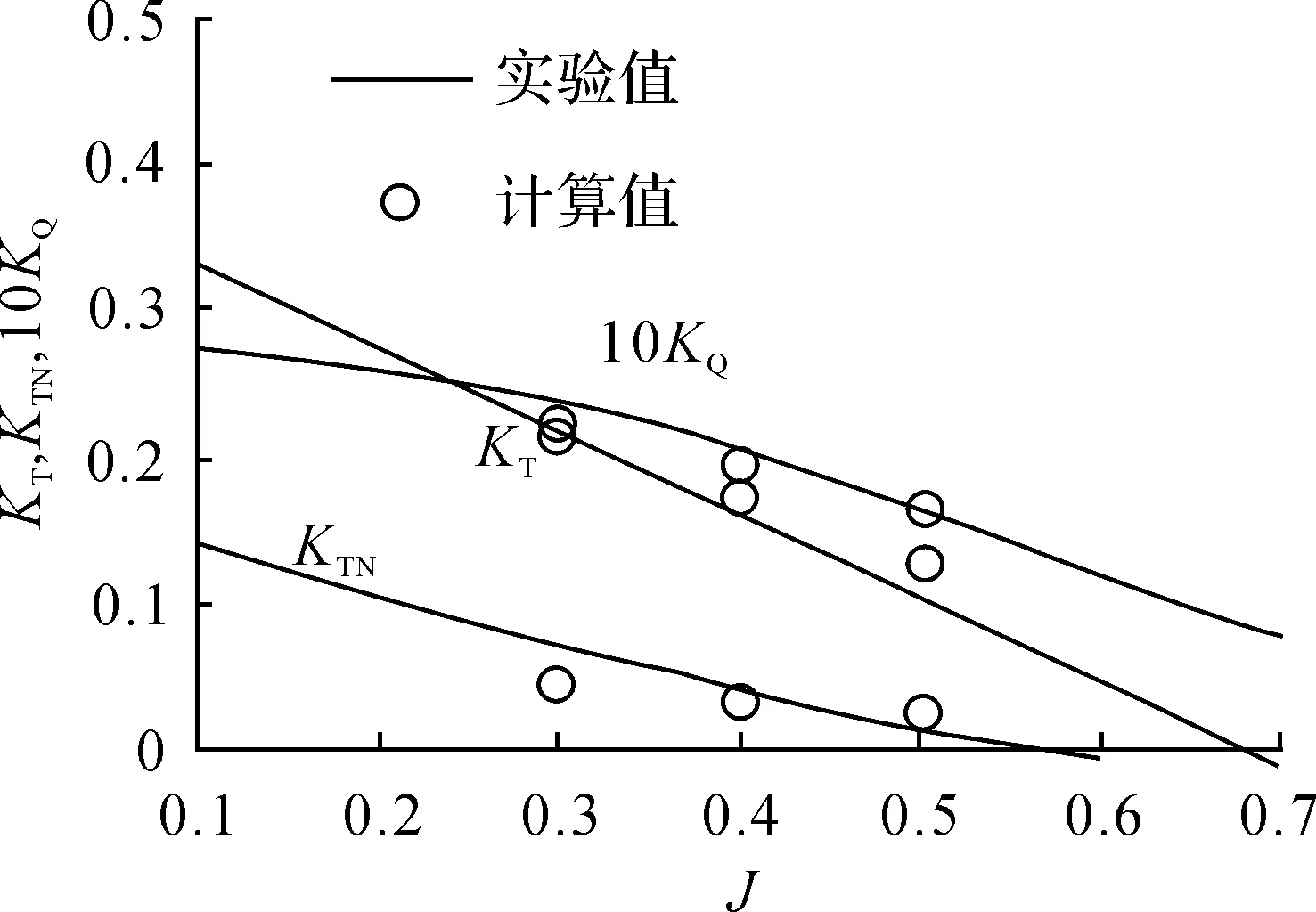
图8 JD7704导管+Ka4-55(P/D=0.8)桨敞水性能比较

图9 JD75导管+Ka4-70(P/D=1.0)桨敞水性能比较
3 结论
本文提供的基于速度势的低阶面元法求解导管螺旋桨定常性能的方法与传统的迭代方法相比所不同的是,该方法将导管和螺旋桨的相互影响计入求解影响系数的过程中,求解时将桨和导管看作一个整体,不用求解导管对桨或桨对导管的诱导速度,避免了迭代过程,使计算时间大大缩减,所得到的结果能够达到比较满意的精度。
[1] Kinnas S A, Hsin C Y, Keenan D P. A Potential Based Panel Method for the Unsteady Flow around Open and Ducted Propellers[A]. 18th ONR[C]. Ann Arbor, Michigan, 1990:21-38.
[2] 蒋志超,王国强,杨晨俊. 导管面元网格划分和影响系数计算的研究[J].船舶力学,2000,10(5):1-8.
[3] 杨晨俊,王国强,杨建民. 导管螺旋桨定常性能理论计算[J].上海交通大学学报,1997,11(11):36-39.
[4] Zhang J H, Wang G Q. Prediction of hydrodynamic performances of ducted controllable pitch propeller[J]. Journal of ship Mechanics, 2002,6(6):18-27.
[5] Liu X L, Wang G Q. A Potential Based Panel Method for Prediction of Steady Performance of Ducted propeller[J]. Journal of ship Mechanics, 2006,6(3):26-35.
[6] 盛振邦. 杨家盛,柴杨业,中国船用螺旋桨系列试验图谱集[M].上海:中国造船编辑部,1983.
[7] 谭廷寿. 面元法预报螺旋桨水动力性能[J]. 武汉交通科技大学学报,1997,10(5):534~541.
[8] 熊 鹰. 非均匀流中螺旋桨空泡即脉动压力的数值和试验研究[D]. 武汉:武汉理工大学,2002.
[9] 叶金铭.考虑自由液面和船体边界条件的螺旋桨脉动压力研究[D].武汉: 海军工程大学,2003.
