日出江淮红胜火，春来江水绿如蓝

　　1立足双基。 试题平稳重基础，清新隽永，颇具内涵，无怪题和偏题。
　　
　　选择题起点低、坡度缓，除第11、12题比较灵活外，其他题几乎是一马平川，有利于学生及早进入状态，增强自信心，这是区别于往年考题的一个显著特点。 填空题比选择题稍难，运算量增大，除第16题比较灵活外，其他仍然是考生熟悉的常规题型。 解答题的前三题都属基础题，其难度与教材的习题难度相当，并且有几道题与课本的习题有关，如第(4)题是由高二数学(上)第11页习题第1题引申得到，第(9)题是由高二数学(下)第74页练习第3题改编得到等，这些题虽源于课本，但又高于课本，这对中学数学教学有很好的导向作用。 纵观试题，个个皆“朴素”，既无高深的知识，又无生僻的技巧。 许多题取材于课本的例、习题的变式题或引申题，利用学生熟悉的知识、问题、及情景做原型，考查三基。 如理科第(1)——(7)、(10)、(13)、(14)、(17)、(18)、(19)、(21)Ⅱ题等，其中第(1)、(5)题是对单一知识点的考查，(5)兼有分类讨论的思想方法；第(2)、(3)、(7)、(10)、(12)、(13)、(14)、(17)、(18)、题用基本的公式、方法均可完成；(4)、(6)、(11)既可直接求解，也可用演绎法——特殊和一般的关系(如特值法)；第(4)题的不必要性，只要令a=1，b=0即可；第(6)题采取验证法较易。 试卷引导我们在教学中跨出题海，真正回到重视基础的轨道。 看看今年考生考完数学的笑脸，你就明白2006年高考复习的起点高了，资料偏难，训练过繁过量。 诚然，我们要正确理解这里的“基础”，它不是指应对考试的基础，即机械重复训练的常规题目，而是指体验知识的形成过程以及对知识本质的顿悟。 对高考试卷分析表明，考生答题失误，并不是因为缺乏灵活的思维和敏锐的感觉，而恰恰因为基础知识、基本理论的掌握上存在缺陷。 因此，2007年的高考复习，必须回归基础，不仅弄懂课本提供的知识和方法，还要弄懂数学定理和公式的推导过程，如理科(20)题用到等比数列求和过程中的“错位相减法”及分类讨论的思想，对习题多作一些推广和变式练习，以揭示知识与方法的联系。 一言敝之，对知识不仅要“广积粮”还要“深挖洞”，既要求全面但更重要是求联系。
　　
　　2突出主干知识的考查。
　　
　　试题对教材各章内容都有所涉及，重点考查高中数学知识的主干内容，如：函数、三角函数、数列、直线与平面、圆锥曲线、概率这六大主干知识，并保持比较高的比例和必要的深度。 如函数约占27分，数列约占12分，三角函数约占27分，概率占17分，立体几何占21分，解析几何占27分，总计约131分。 鉴于此，2007年的备考要以熟练掌握主干知识为龙头，立足于通性、通法的训练，归宿于数学思想和方法的强化。
　　重视主干知识的形成，必然要理清主干知识的脉络，分析主干知识的内涵、外延和交汇。 充分重视主干知识的支撑作用，以主干知识为支柱，构建知识网络。 如在函数的复习中一定要链接导数，在向量的复习中要融入平面几何、立体几何、解析几何、三角函数和数列，不等式的复习中倾注函数、数列、向量和解析几何，排列、组合与概率和概率统计二合一为一章进行复习等等。 如此这般渐渐模糊知识模块和章节的界限，最后达到交汇统一。
　　
　　3加大新旧知识整合的力度。
　　
　　向量、概率、导数等新增内容工具性强，应用广泛，它们的引入给传统内容注入了新的活力。 体现新旧内容的结合，突出使用新观点、新方法来解决传统问题，在知识的交汇处设计试题是高考题的一大特点：如第(2)题集合、不等式、函数的相濡以沫；第(4)题不等式与简易逻辑的渗透；第(7)题是曲线的切线与导数几何意义的结合；第(10)题的线性规划与几何的牵手；第(12)题的立体几何与排列组合、概率的不期而遇；第(18)题是概率与应用题的联袂；第(19)题为立体几何与向量的姻缘；第(20)题是抽象函数、分段函数、函数性质的交汇；第(21)题为数列与函数导数的狭路相逢；第(22)题直线与双曲线、平面几何的群英荟萃，都是知识交汇的经典之作。 试题在向量、概率、导数、线性规划等新增内容突出了对导数与相关知识交汇考查的力度，削弱了对向量的考查。 体现导数的工具性，更强调导数与其他知识间的联系。 导数的工具性考查力度有余，向量的综合性整合幅度明显不足。 第(19)题立体几何解答题仍采用“一题两法”的命题办法，显然研究垂直、夹角等问题向量法更易上手。
　　
　　4深化能力立意，突出数学思想方法的考查。
　　
　　如理科的第(2)、(6)、(8)、(9)、(11)、(16)、(20)、(21)题是对思维能力中的直觉猜想能力的考查；第(3)、(12)、(14)、(16)、(19)考查了空间想象能力，主要体现在对文字语言、符号语言和图形语言的互相转化，以及对图形的识别、理解和加工，与运算能力、逻辑思维能力相结合；理科第(21)题是对思维能力的模式构建能力的考查；第(15)、(21)题是对思维能力中的归纳想象、演绎证明能力的考查等等。
　　对数学思想和方法的考查主要涉及数形结合的思想方法，如理科的(6)、(7)、(10)、(19)、(22)等；转化与化归的思想方法如(4)、(6)、(9)、(11)、(12)、(20)等；如(9)题是球内接正八面体的问题，学生不熟悉此情景，但由对称性可知：即为棱长相等的正四棱锥内接于半球的问题，从而化归为较熟悉的正四棱锥的问题；分类讨论的思想方法如理科(5)、(16)、(18)、(20)题等；函数与方程的思想方法如(13)、(17)、(20)、(21)、(22)等；又(20)、(21)、(22)分别考查了换元法、数学归纳法、待定系数法、错位相减法、导数法等。 这些思想方法是平时教学中反复应用和锤炼的，也是学生耳热能详的，关键在考场上能否抓住本质，应用恰当的思想方法，以简捷、明快的思维发现解决问题的途径。
　　2007年备考中应重视数学基本思想方法的渗透和应用。 尤其要重视配方法、换元法、待定系数法、数学归纳法和数形结合法等常用数学技能和方法；分析法、综合法、归纳法、演绎法和反证法等常用的逻辑推理方法；函数与方程、变换与转化、分类与归纳、数形的结合与分离、定常与变化的对立和统一等重要的数学思想和方法。 以夯实主干知识为原点，以熟练数学思想方法为支点，以提升能力为驻点，不遗余力地培养学生较高的思维层次中的探索能力、直觉思维能力、合情推理能力、创新能力。
　　
　　5出题思路灵活多变，试题形式多样。
　　
　　试卷注意用学生熟悉的、常见的背景，重新设计考查数学思想方法、数学思维品质的试题，跳出平时的模拟试题和复习资料上的题目，试题背景设计公平，贴近学生实际，问题设计入口宽、层次清、方法多，使不同的学生都能在公平的背景下展示真实的水平。如(11)、(12)是知识载体创新，(16)是开放型创新题；理科第(20)题有高等数学的背景，尤其是第(Ⅱ)设问奇特，突破常规、抽象性强、回避了复习资料，学生鲜见，在短时间内能否顺利实现a与x的换位是解题的关键，这要求学生对函数概念有深刻的理解和把握，并能灵活应用，它终使“无数英雄竞折腰”；这属解法创新。理科卷将此题位置调前，考查学生的应变能力及个性品质。第21题是一个数列题，所给递推关系式比较复杂，字母较多，快速将其变为
　　
　　
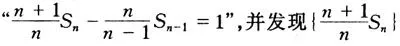
　　是等差数列不是件容易的事。而第(Ⅱ)问又融入了导数、增加了字母p，抽象程度越来越高，难度增大。第22题融双曲线、平行四边形、方程(组)、根与系数的关系、弦长公式等于一体，具有知识点多、覆盖面广、运算量大、综合性强的特点。顺利求解这三大题，没有较强的理性思维能力是不行的。稳中求变，变中求新一直是高考命题追求的目标，今年也不例外。如选择题第(9)题涉及“正八面体的外接球”，一变过去“正面四体的外接球”的老面孔，给人以新鲜感；选择题第(11)题设问方式新颖，求解方法灵活；填空题第16题融阅读、理解、识图、发现、猜想于一体，具有背景新、内容新、方法新的特点；尤其是第20题的第(Ⅱ)问，以高等数学知识为背景设计问题，抽象函数关系式的结构简洁，解法巧妙，数学思想方法蕴涵其中。这四题朴实大方，堪称上乘之作，是整套试卷的创新亮点之所在，它们有效地考查了学生的创新能力。
　　2007年高考复习建议：时时关注新版《考试说明》，《考试说明》指出——选择题、填空题和解答题题目的个数分别为10—12、4、6个，说明选择题存在10个题的可能。
　　其次是关注高等数学初等化。一则高考命题者大多来自高校专家；再则高考是一种选拔性考试，它要考查学生进入高校继续学习的潜能。因此高考题中几乎每年都有几道以高等数学为背景的题目。
　　6不等式受冷遇。去年高考数学全国卷(Ⅰ)多次考查不等式，其中理科压轴第(2)问是一道不等式证明题，它难倒不少考生，但今年的考题明显冷落了不等式。如此大的反差，出人意料，它提醒教师：不能引导学生猜题押题，明智的选择是按考纲要求进行系统地复习。
　　7对向量考查力度不够。向量是新增的重点内容，它融代数特征和几何特征于一体，能与三角函数、函数、解析几何、立体几何自然交汇、亲密接触。向量作为代数与几何的纽带，理应发挥其坐标运算与动点轨迹、曲线方程等综合方面的工具性功能。今年，不少省、市有这方面的高考试题，实属情理之中；而我省的高考卷中，仅有第6题和第14题两个基本题，第19题立体几何也可以运用向量解法，但传统方法更为简单，无法凸现向量的价值，没有出现向量与解析几何的综合题。向量处没有新动作，有些出人意料，让人遗憾。因此加大对向量的考查力度，充分体现向量的工具价值和思维价值，应该是今后高考命题的发展趋势。
　　8该套题两多一少。“两多”是三角函数题多、解析几何多；“一少”是数列题少。三角函数是新教材的软肋，不仅是因为新教材删除了旧教材中一半以上的三角公式，课时比例大大降低，而且很多知识点的要求层次也降低了，所以高三师生都不约而同到认为三角是最轻松的一章，是唯一可以稍事休息和小憩的场所。然而今年高考题却在三角一章中直接出了三小一大合27分题，与公认的函数(27分)老大哥平起平坐了!解析几何也有三小一大计27分，直接叫板函数的统治地位；而传统重点内容、在学生心目中最规矩的数列只出了一个12分的大题。
　　看来，2007年的高考复习还得均衡发展，教材中的每一个章节内容都可能成为高考的热点和重点，来的都是客，一个也不能少，哪个也不能轻视，不能人为地划定三六九等，要一视同仁，稳扎稳打。最后还要关注创新题，尽量少用几十年不变的陈题。如从报刊中涉猎新题，通过新题归纳解题的思维方法，激发头脑的思维风暴；关注题型的单向发展，重视横纵联系；拓展新题的思想方法，加强多元交汇，使对知识的掌握达到“鹰击长空，鱼翔浅底”的境界。