巧哉，质数幻方

肖乐农

幻方的研究由来已久，古老的洛书是研究幻方的最早神话.由于幻方妙趣横生，吸引着众多的爱好者，研究成果层出不穷.幻方的种类形形色色：回文幻方、积幻方、双重幻方、六角幻方、马步幻方……每一款都构思奇巧，但最巧的是质数幻方.

质数是一种很难驾驭的数.它分布混乱，无穷无尽.可是，数学家们竟然使质数与具有均衡对称美的幻方联起手来，巧妙地构造出了一个个质数幻方.

你看，图１就是一个三阶质数幻方.它不但９个数都是质数，而且每行、每列及两条对角线上的三个数之和都等于２６７.我们来看看构成这个幻方的９个质数：

１１，７１，１３１；２９，８９，１４９；４７，１０７，１６７.

原来这９个质数可分为３组，每组相邻两数的差（后一个减前一个数）都是６０，每一组的三个质数都不在同一行、同一列.

怎么样？挺巧吧．其实，真正的巧事还在后头.

有一次，一位宫廷数学家领到了一年的工资，共１ ３５０个银元.他做游戏似地将这些银元分成不相等的９堆，然后摆成一个幻方，并给国王看了.这是一位很喜欢研究质数和幻方的国王，他看后非常赞赏，但觉得这些堆中没有一堆是质数，有些遗憾.

这时数学家对国王说：“只要国王奖赏我９个银元，我在每堆中各加１个银元，幻方中的每一堆银元就都是质数了.”国王发现果真如此，就高兴地奖赏了数学家９个银元，并加到幻方之中.

站在旁边的一个宫女对数学家说：“如果我在每一堆中拿走相同数目的银元，使幻方中的每一堆仍是质数，您同意我带走拿出来的银元吗？”数学家觉得宫女不懂数学，再加上这事也不太可能，便答应了.于是，宫女从每堆中拿走２个银元.这时，国王和数学家发现，幻方中剩下的每堆银元确实都是质数，那１８个银元只好让宫女带走了.

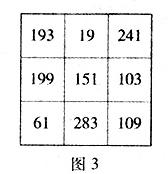
那么，数学家一开始摆的幻方是什么样呢？以后两次变化又是怎么样呢？请看如图２、图３、图４的三个幻方：

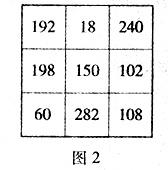
原来后两个质数幻方是由９对孪生质数构成的，一个由每对孪生质数中较大的那个质数构成，另一个由每对孪生质数中较小的那个质数构成.

质数幻方的排序之巧，构造之难，挑战着众多的数学家：美国数学科普大师马丁·加德纳曾悬赏１００美元，奖给第一位利用连续质数造出三阶幻方的人.注意，９个质数必须是连续的，中间一个也不许跳过.这道题可够难的，没有点功力根本无法办到.

俗话说重赏之下必有勇夫（可惜不是什么重赏）．１９８８年，美国的一位幻方爱好者纳尔逊，利用加利福尼亚大学的克雷超级计算机，通过巧妙的程序设计，一举解决了这个难题，并且一下子提供了２２个答案，超额完成了任务.其中数字最小的一个如图５所示.

纳尔逊坦言，他的程序并不能证明这是最小解，但要找到更小解的概率几乎接近于零.