基于不同物理视角对比分析法的教学应用

摘"要：“电磁学”是学生认识场物质（如电场和磁场）的开始，可实现由力学机械运动的直观分析思考到电磁场物质抽象分析论证的思维方式转变。因此，电场和磁场相关内容的教学是“电磁学”课程中的重点与难点。在本文中，以电场叠加原理、电场强度通量、电势三种不同的物理观念视角为线索，介绍了无限长直导线电场强度的三种推导方法，并对比分析了其中所涉及的不同物理思想和数学方法。同时，本文重点探讨了对比分析方法在“电磁学”教学中的应用，深入研究了这些方法所展现出的教学价值，有利于不断开拓教学新思路、革新教学方法与模式，同时能够有效提升学生学习的主动性和效率，从而促进“电磁学”课程教学质量的持续提升。

关键词：电磁学；课堂教学；对比分析方法

1"绪论

“电磁学”是学生认识场物质的开始，可实现由力学机械运动的直观分析思考到电磁场物质抽象分析论证的思维方式转变，是面向高等学校物理学专业学生的一门重要基础专业课程［1］。在教学过程中，笔者也发现存在一些教学难点。以笔者授课时使用的梁灿彬等人主编的《电磁学》教材为例，该教材分别以叠加原理、通量、环量等概念，多角度、系统性地阐述了电场的性质，通过具有不同物理场景的例题（如有限长直导线、无限大带电平面及均匀带电球壳等）来深化这三个物理概念的讲解。但是由于学生首次系统性地接触到“场”的概念及其相关处理方法，因此容易将其看作完全独立的内容来学习，而且上述例题中涉及大量的积分运算，部分同学会错误地把“电磁学”当成又一门高等数学课，因此并未注意到这三个物理概念之间的区别与内在联系，从而难以建立系统的、完整的知识体系和框架。

基于上述讨论，本文拟从无限长直导线电场强度的计算入手，以电场叠加原理、电场强度通量、电势三种不同的物理观念为线索，介绍了无限长直导线电场强度的三种计算方法，对比分析其中所涉及的不同物理思想和数学方法，以及各自所具有的优势与不足，进而帮助学生更加全面且深入地理解、记忆电场相关知识，建立系统的、完整的知识体系和框架，有效提升学习的主动性和效率。同时，探讨了对比分析方法在“电磁学”教学中的教学价值，有助于不断开拓教学新思路、革新教学方法与模式，激发学生的学习兴趣，从而促进“电磁学”教学质量的持续提升［23］。

2"不同物理观念视角下无限长直导线电场强度公式的推导

2.1"电场叠加原理法

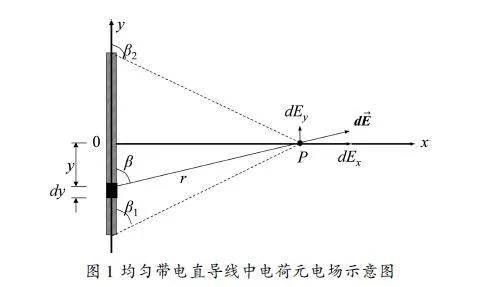
图1"均匀带电直导线中电荷元电场示意图

现在真空中有一长为l、电荷密度为λ的均匀带电直导线，建立如图1所示坐标系。和中学物理不同的是，此时带电直导线具有一定的长度且不能直接被视为点电荷，因此不能直接用点电荷的电场强度公式直接得到电场强度。于是我们采用微元法进行处理：在距离坐标原点为y距离处取一个长度为dy的电荷元，其电量为λdy，其在导线一旁距离为x的P点处产生的元电场强度为：

dE→=dq4πε0r2e→r==λdy4πε0r2e→r

该元电场强度在x轴和y轴上的分量分别为：

dEx=dEsinβ=λdy4πε0r2sinβ

dEy=dEcosβ=λdy4πε0r2cosβ

我们知道，电场的定义为试探电荷受到的电场力与试探电荷带电量的比值，由于电场力是矢量，服从矢量叠加原理，容易证明电场强度也遵循叠加原理。根据电场强度叠加原理可知，在整个导线一旁距离为x的P点处产生的总电场强度可通过对元电场强度进行积分得出：

Ex=∫β2β1dEx=λ4πε0a（cosβ1－cosβ2）

Ey=∫β2β1dEy=λ4πε0a（sinβ2－sinβ1）

上式为有限长直导线的电场强度计算结果，当带电直导线为“无限长”时（l=∞），并且λ保持为常数，此时积分上下限β1=0，β2=π，从而得到无限长直导线一旁距离为x的P点处产生的总电场强度为：

E→x=λ2πε0ai→

Ey=0

2.2"高斯定理法

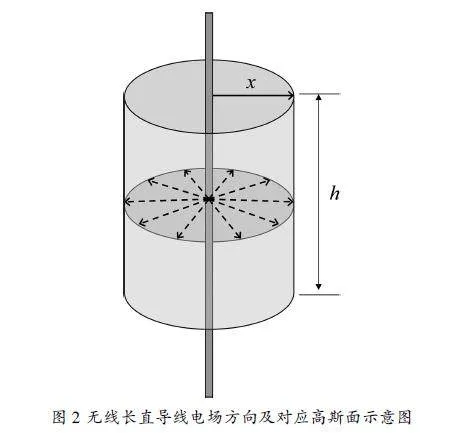
图2"无线长直导线电场方向及对应高斯面示意图

由于静电场是一个矢量场，因此可以引入电场强度通量来表征静电场在某一曲面上电场的总体分布情况。由于电场是由电荷激发的，因此电场强度通量应该与电荷存在某种物理上的联系，高斯得到了电荷和电场强度通量之间的数学关系，即静电场通过任意闭合曲面的电场强度通量等于包围在高斯面内电荷量代数和除以ε0SE→·dS→=1ε0∑iqi，这便是静电学中著名的高斯定理。因此，我们可以通过求解此微分方程来计算带电体的电场强度。同样以无限长直导线为例，并以无限长直导线为轴，做一个半径为x，高度为h的圆柱面，如图2所示。在圆柱侧面任取一场点P，由对称性分析可知，只有沿半径方向的电场强度分量不为零，且圆柱面上各点电场强度大小都相等，方向与此柱面垂直。

按照电场强度通量的定义，无限长直导线产生的电场强度在此圆柱面上的通量ΦE为

ΦE=SE·dS=ΦE侧面+ΦE底面

其中电场强度方向与上、下底面平行，因此上、下底面的电场强度通量为零。同时，电场强度方向与侧面法线方向平行，因此侧面的电场强度通量为：

SE·dS=E·2πxh

同时包围在此圆柱面（或高斯面）内电荷量代数为λh。

由高斯定理知，通过任意闭合曲面的电场强度通量等于包围在高斯面内电荷量代数和除以ε0，从而解得无限长直导线一旁距离为x的P点处产生的电场强度为：

E→=λ2πε0xe→r

2.3"电势法

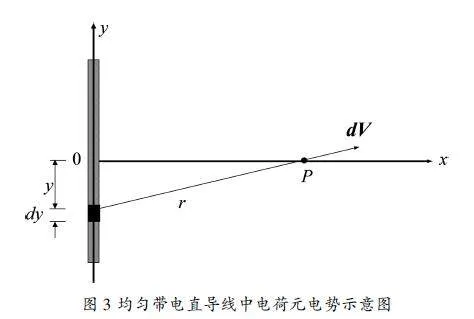
图3"均匀带电直导线中电荷元电势示意图

由于静电场是一个保守场，静电场做的功只与带电物体运动的初末位置相关，可以推导出静电场强沿任意闭合曲线的环流为零（即静电场的环路定理），同样意味着静电场具有有势性，进而可以引入电势来描述静电场。我们讨论在真空中有一长为l、电荷密度为λ的均匀带电直导线，建立如图3所示坐标系。同样，我们采用微元法进行电势计算，在距离坐标原点为y距离处取一个电量为λdy的电荷元，其在导线一旁距离为x的P点处产生的元电势为：

dV=dq4πε0r=λdy4πε0x2+y2

由于电势也遵循根据电场强度叠加原理，因此在整个无限长直导线一旁距离为x的P点处产生的总电势可通过对元电势进行积分得出：

V=∫+∞－∞dV

=∫+∞-∞λdy4πε0x2+y2

=limz→∞λ4πε0ln2（y2+yy2+x2+x2）x2

不难发现，无限长直导线在P点处的电势是发散的。由于带电直导线为“无限长”，因此满足近场条件近似条件（yx），于是上式可改写为：

V=limy→∞λ2πε0ln2y－λ2πε0lnx

由于电场等于电势的负梯度（E=－SymbolQC@

V），因此，无限长直导线一旁距离为x的P点处产生的电场强度为：

E→=－Vxi→+－Vyj→=λ2πε0xi→

3"不同物理观念视角下求解无限长直导线电场强度的对比分析

通过对上述例题的对比分析可知，以电场叠加原理、电场强度通量、电势三种不同的物理观念为线索，均可以对无限长直导线的电场强度进行求解，并且可以得到相同的结论［45］。但是，不难发现，这三种方法均有各自的特色与使用范围。首先，电场叠加原理是一种最基础、最普适的电场强度计算方法，只是电场是一个矢量，因此在计算电场时，既要考虑电场的大小，也要考虑电场的方向，需要将电场强度投影到各个坐标轴上，对其分别进行计算。特别是处理一些具有复杂形状的带电体的电场强度计算问题时，需要具备一定的几何空间想象力。其次，利用高斯定理求解电场强度，可以通过选择合适的高斯面，使得某一区域或者整个高斯面上的电场强度E→为常数，并且电场强度E→和dS→方向平行（或者垂直），这样就可以将复杂的积分方程转化为普通的代数方程，不使用微积分等高级数学知识也可以计算电场强度。但是这种方法只能处理具有高对称性体系的电场强度计算［如均匀带电的球面（体），无限长均匀带电的直线、圆柱面（壳）和无限大的均匀带电平面等］，具有很大的局限性。与电场叠加原理相似，通过计算电势来求解电场强度同样需要微元法思想、叠加原理和微积分知识，但是由于电势是一个标量，因此只需要计算其大小，省去了其空间方向的判断与思考，最后通过数学梯度运算，就可以得到电场强度的大小与方向。但是，从上面例题不难发现，由于电势的大小是与电势零点的选取有关的，因此计算出的无线长直导线的电势是发散，想进一步得到电场强度，还得做一些数学上的近似和处理。总而言之，物理观念视角下计算电场强度的方法各有千秋，各有善于处理的情景。但是通过分析与对比这三种方法，可以有效地将电场相关知识（电场叠加原理、电场强度通量、电势）串联起来，学生能够更加全面且深入地理解、记忆电场相关知识，建立系统的、完整的知识体系和框架。

结语

本文分别从电场叠加原理、电场强度通量、电势三种不同的物理观念视角出发，结合实例介绍了无限长直导线电场强度的三种推导方法，对比分析了三种方法中所涉及的不同物理思想和数学方法，以及各自所具有的优势与不足。同时，重点探讨了对比分析方法在大学物理“电磁学”教学中的应用，研究了它们的教学价值，有利于学生有效地将电场相关知识融会贯通，从而更加全面且深入地理解、记忆电场相关知识，建立系统的、完整的知识体系和框架，从而能够在有限的教学时间内提升学生的学习效率的。在“电磁学”课程的教学中，应用对比分析方法展现了其独特的重要性。这种方法不仅为教师提供了一个有效的工具，帮助学生更清晰地理解复杂的“电磁学”概念。同时，运用对比分析可以开拓教学的新思路，激励教师在教学过程中不断创新教学模式和方法。这种创新的教学方式不仅有助于深化学生的理解，还有助于激发他们的学习兴趣，使他们在探索电磁现象的过程中，进一步培养逻辑思维能力和问题解决能力。综上所述，通过持续应用对比分析方法，显著提升了“电磁学”课程的教学质量，从而使学生在学习过程中受益匪浅。

参考文献：

［1］张平丽，徐仕翀，邓健男，等.电磁学课程教学改革与创新设计［J］.物理通报，2024（05）：2730.

［2］王琳，陈荣军.对称性视角下大学物理课程教学创新研究：以“电磁学”为例［J］.广东技术师范大学学报，2024，45（03）：4348.

［3］郭奕玲，沈慧君.物理学史［M］.2版.北京：清华大学出版社，2005.

［4］梁灿彬，秦光戎，梁竹健.电磁学［M］.4版.北京：高等教育出版社，2018.

［5］赵凯华，陈熙谋.电磁学［M］.3版.北京：高等教育出版社，2023.

作者简介：陈是位（1991—"），男，汉族，甘肃张掖人，讲师，博士研究生，研究方向：凝聚态物理。

*通信作者：梁世恒（1986—"），男，汉族，河北邢台人，教授，博士研究生，研究方向：凝聚态物理。