基于SMOTified-BRF模型的地球化学金矿化异常预测研究

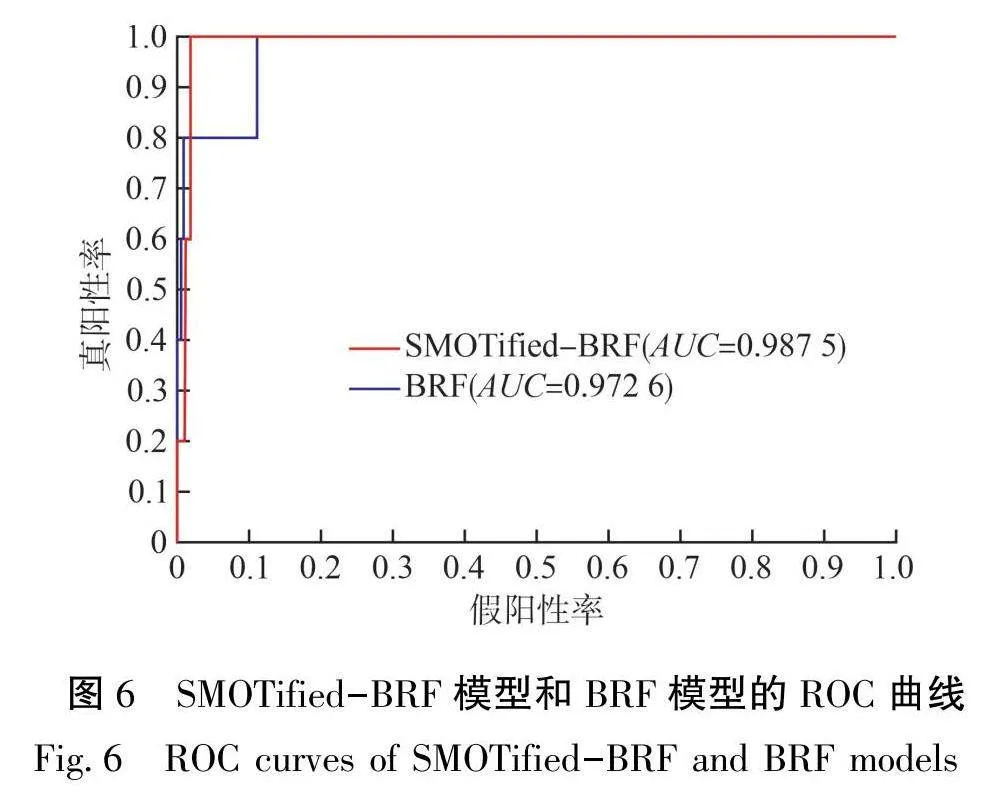
摘要：矿产勘查既是新质生产力的重要组成，又是推动新质生产力发展的重要力量。为了改善矿产勘查中金矿化预测面临的由于已知矿化样本数量少导致的样本类不平衡问题及矿化信息稀缺问题，提出SMOTified-BRF模型，该模型使用SMOTE方法对极少数已知矿化样本进行数量增强并使用平衡随机森林方法进行预测。以汉滨—旬阳地区为研究区，对水系沉积物地球化学数据分别使用SMOTified-BRF模型和BRF模型进行金矿化预测效果和模型性能对比研究。研究结果表明：SMOTified-BRF模型的AUC值（0.9875）高于BRF模型的AUC值（0.9726），且在约登指数指示的最优阈值下SMOTified-BRF模型预测的矿化面积占比（1.95%）相较于BRF模型（12.23%）更小，说明SMOTified-BRF模型相比于BRF模型具有更准确高效的金矿化异常预测性能。

关键词：金矿化；异常；预测；平衡随机森林法；SMOTE;地球化学；汉滨—旬阳地区

中图分类号：TD11 P618.51文章编号：1001-1277（2025）01-0011-09

文献标志码：A doi：10.11792/hj20250103

2023年9月，习近平总书记在主持召开新时代推动东北全面振兴座谈会时提出，积极培育战略性新兴产业和未来产业，加快形成新质生产力，增强发展新动能。矿产勘查处于矿产资源产业链供应链的最前端，关系到现代化产业体系发展的能量与物质基础，在发展新质生产力中具有重要的基础地位和支撑作用。矿产勘查通过发现和查明矿产资源，既为现代产业体系构建提供物质基础，又是现代产业体系的一部分，自身生产力的提升也是发展新质生产力的重要内容，对于保障资源安全，增强发展新动能具有重要意义3。作为矿业行业新质生产力的重要组成，人工智能找矿方兴未艾。

地球化学数据是一类重要的找矿信息，在矿产勘查与评价中具有非常关键的作用。基于地球化学数据处理的人工智能方法研究一直是地球化学研究领域的热门方向之一。使用先进的方法从大量地球化学数据中挖掘矿致信息并进行矿化预测，有助于推动矿产勘查发展。

成矿系统的复杂性及成矿作用的多期多阶段特征导致地球化学数据往往具有复杂、未知的空间与频率分布特征。近年来，由于机器学习、深度学习方法在处理具有复杂分布特性非线性数据的分类与回归预测问题中具有良好表现”，越来越多的学者将先进的机器学习、深度学习方法引入地球化学矿化预测领域，如支持向量机、随机森林、受限玻尔兹曼机等。然而，地球化学数据中的已知矿化样本（阳性样本）数量稀缺背景样本（性样本）数量占比大，使用一般的机器学习和深度学习方法对类不平衡的地球化学数据进行矿化预测面临着挑战。已有学者将关注点放在解决地球化学数据类别、数量不平衡问题的方法研究上，此类研究包括从数据处理角度引进各类采样方法平衡数据类别比例和从算法角度引进类不平衡学习集成算法进行数据的分类任务处理。例如，SHAYILAN等利用合成少数类过采样技术进行过采样以平衡数据类别比例，CHEN等引入自定步集成框架来处理类不平衡问题。

考虑到已有模型大多单独关注从数据或者算法角度解决样本类不平衡的问题，因此本研究同时从数据处理角度和算法角度出发，结合合成少数类过采样技术（Synthetic Minority Oversampling Technique， SMOTE）和平衡随机森林算法（Balanced Random Forest，BRF），提出采用SMOTified-BRF模型进行 类不平衡地球化学数据的矿化预测研究。平衡随机森林算法是一种类不平衡学习集成算法，它在随机森林算法（Random Forest，RF）的基础上引进了随机欠采样策略[20]。平衡随机森林算法在训练每棵决策树（Decision Tree，DT）之前通过对数量占多数的类别数据进行随机欠采样，以此来平衡用于训练每棵决策树的训练子集类别比例。平衡随机森林算法建立在传统随机森林算法的基础上，使用多棵决策树的集成来提高预测的准确性和稳定性。平衡随机森林算法不仅具有随机森林算法的准确率高、善于处理离散数据等优点[2]，同时更善于处理类不平衡数据。平衡随机森林算法适合用于类不平衡地球化学数据的异常识别与分类。然而，在已知矿化样本极度稀缺的地球化学数据中，平衡随机森林算法在训练每棵决策树前为了构建类别平衡的训练子集，会随机剔除过多的背景样本，导致丢失具有重要信息的背景样本。同时，已知矿化样本的稀缺容易导致决策树在学习已知矿化样本特征的过程中出现过拟合问题。因此，本研究引进SMOTE，对地球化学数据中的已知矿化样本进行数量增强，并使用增强后的地球化学数据作为平衡随机森林算法的训练集，构建基于SMOTE增强的平衡随机森林金矿化预测模型（SMOTified-BRF模型）。

本研究以汉滨—旬阳地区作为研究区，对1：5万水系沉积物地球化学数据分别构建SMOTified-BRF模型和BRF模型进行金矿化预测和对比研究。研究结果证明，SMOTified-BRF模型预测的金矿化区比BRF模型预测的金矿化区具有更小的范围和更高的准确性。

1地质概况

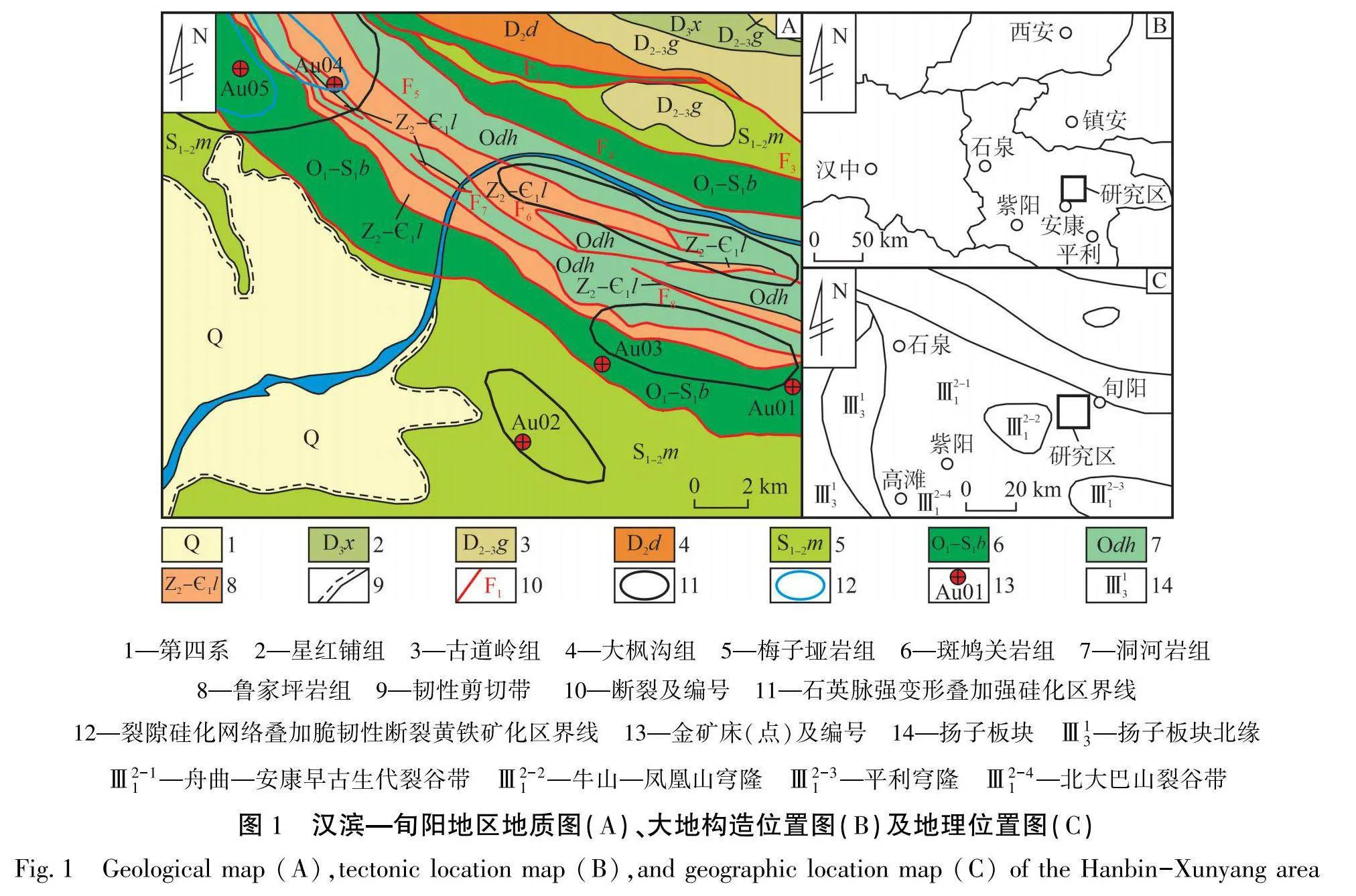
汉滨—旬阳地区位于陕西省安康市（见图1-C），大地构造位置位于秦岭地块南缘，属扬子板块（Ⅲ）秦岭—大别山新元古代—中生代造山带（Ⅲ₁）北大巴山—西倾山早古生代裂谷带（Ⅲ²）舟曲—安康早古生代裂谷带（Ⅲ²-1）（见图1-B）。研究区主要发育断裂有北西向展布脆性断裂，近南北向次级小型脆性断裂及北西向脆韧性剪切带，由北向南划分为赵家山—斜山寨滑脱逆冲推覆体、将军山—烂木沟滑脱逆冲推覆体和安康断陷盆地3个次级构造单元。研究区出露地层有寒武系鲁家坪岩组（Z₂-E₁l）、箭竹坝组（Z₂-E₁j），奥陶系洞河岩组（Odh），奥陶系—志留系斑鸠关岩组（O₃-S₁b），志留系梅子垭岩组（S₁-2m），泥盆系大枫沟组（D₂d）、古道岭组（D₂-3g）、星红铺组（D₃x），以及第四系（Q）等（见图1-A）[22]。研究区内火山岩建造不发育，仅在图幅中部神滩河—烂木沟一带鲁家坪岩组中有少量出露；侵入岩极不发育，未见岩体出露，仅见酸性岩脉出露[23]。研究区主体为变质岩建造区，占70%以上，气-液变质岩不可见，热接触变质岩极不发育，变质岩主要为区域变质岩和动力变质岩。

研究区共发现典型金矿床（点）5处（见表1），成因类型均为韧性剪切带型，主要分布于区域性韧性剪切带两侧的次级构造带中。区域内金矿床（点）主要分布于斑鸠关岩组、洞河岩组、梅子垭岩组、鲁家坪岩组地层中。含矿岩性主要为含碳黑云母绢云母石英片岩、绢云石英片岩、硅质板岩、碳质板岩等。研究区内与金成矿关系密切的蚀变主要有硅化、绢云母化、黄铁矿化等，表现为蚀变越强，规模越大[24]。

2地球化学数据预处理与指示元素选择

研究区的地球化学数据来源于安康幅1：5万水系沉积物调查样本，样本数量为1828件。对样本测试了14种元素，分别为Au、Ag、As、Bi、Cd、Co、Cr、Hg、Mo、Pb、Zn、W、Sn、Ni。对1828件水系沉积物样本的14种元素数据进行网格化处理，为每种元素生成379×476（180404）个网格数据。

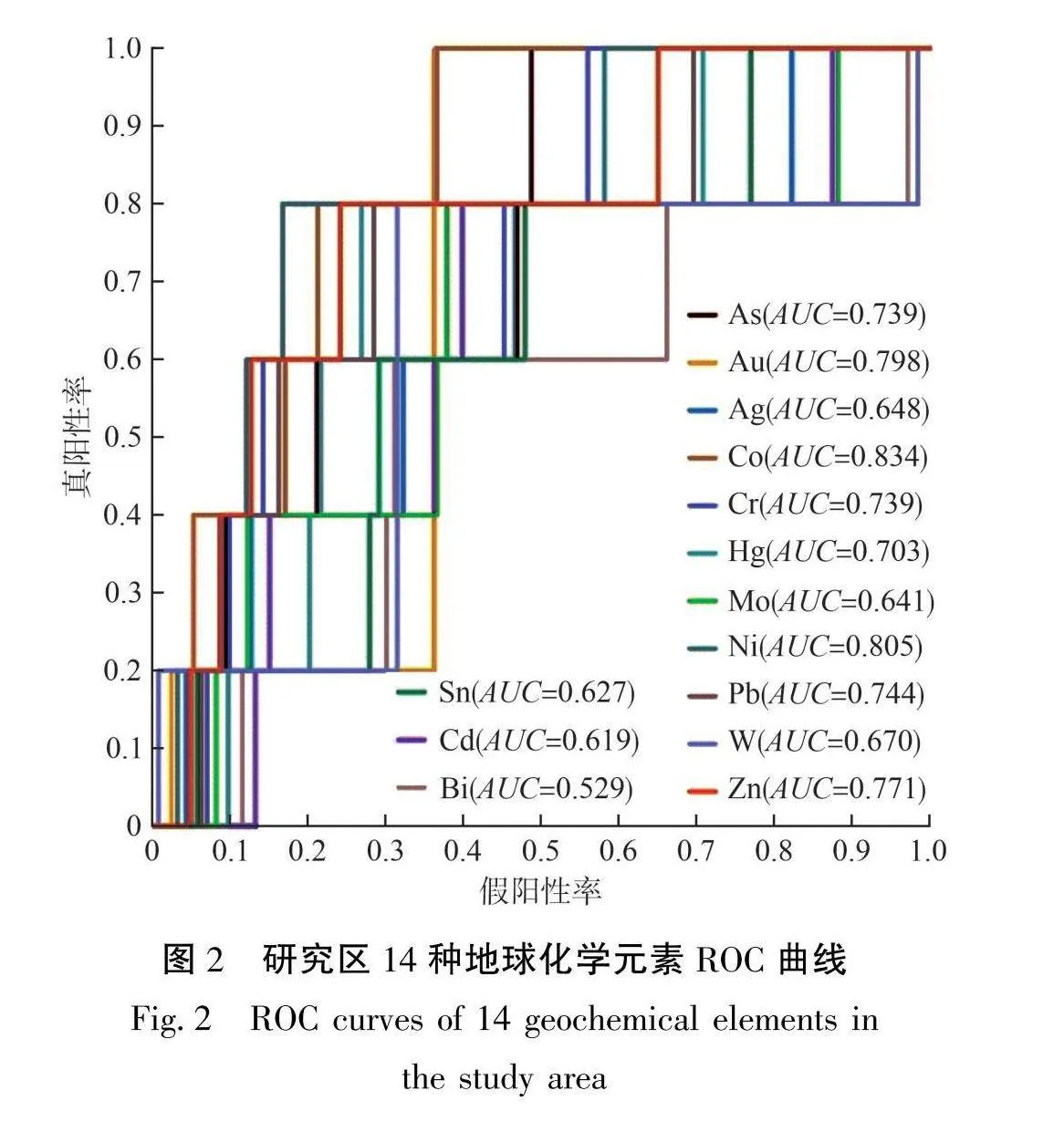
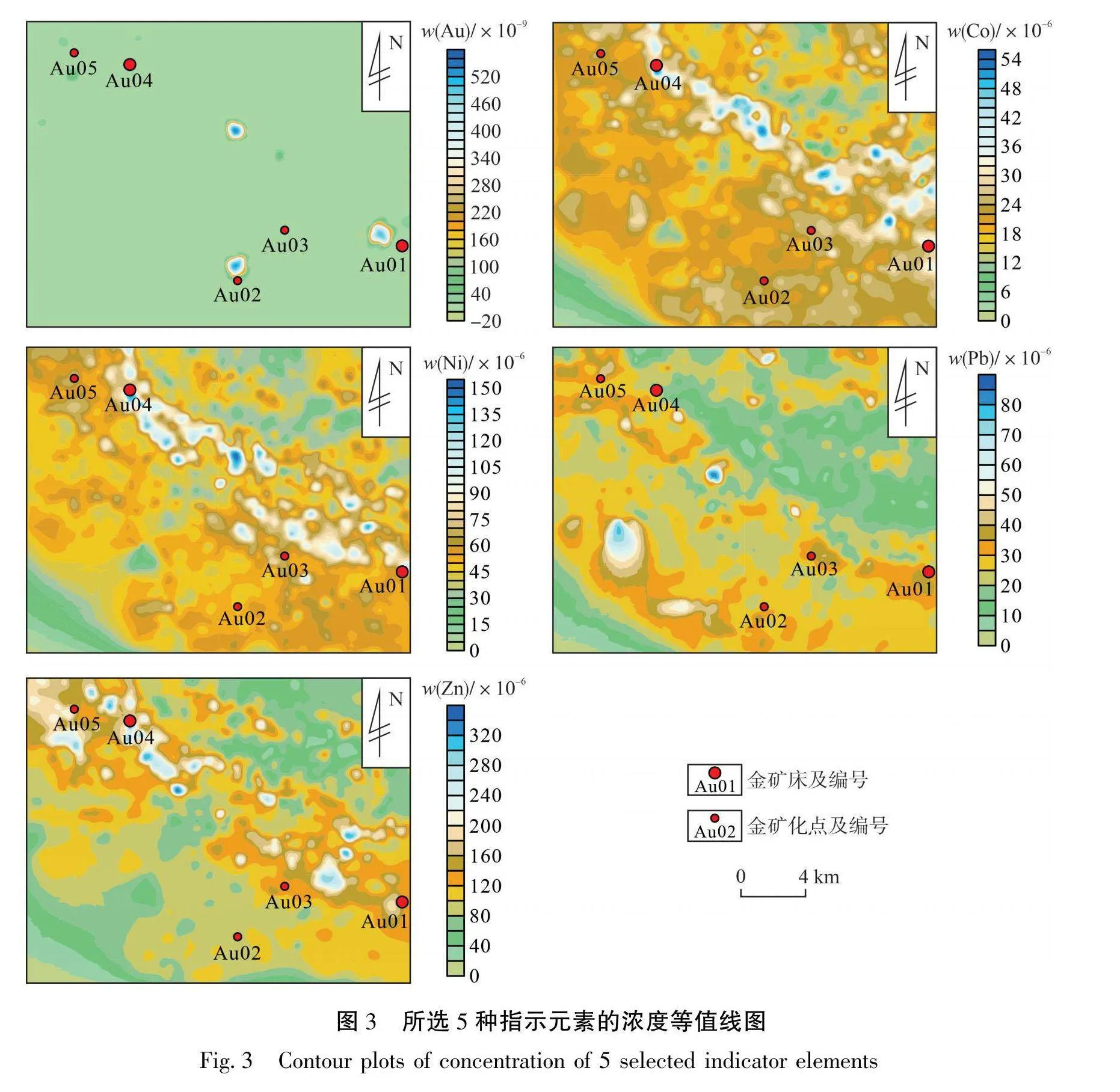
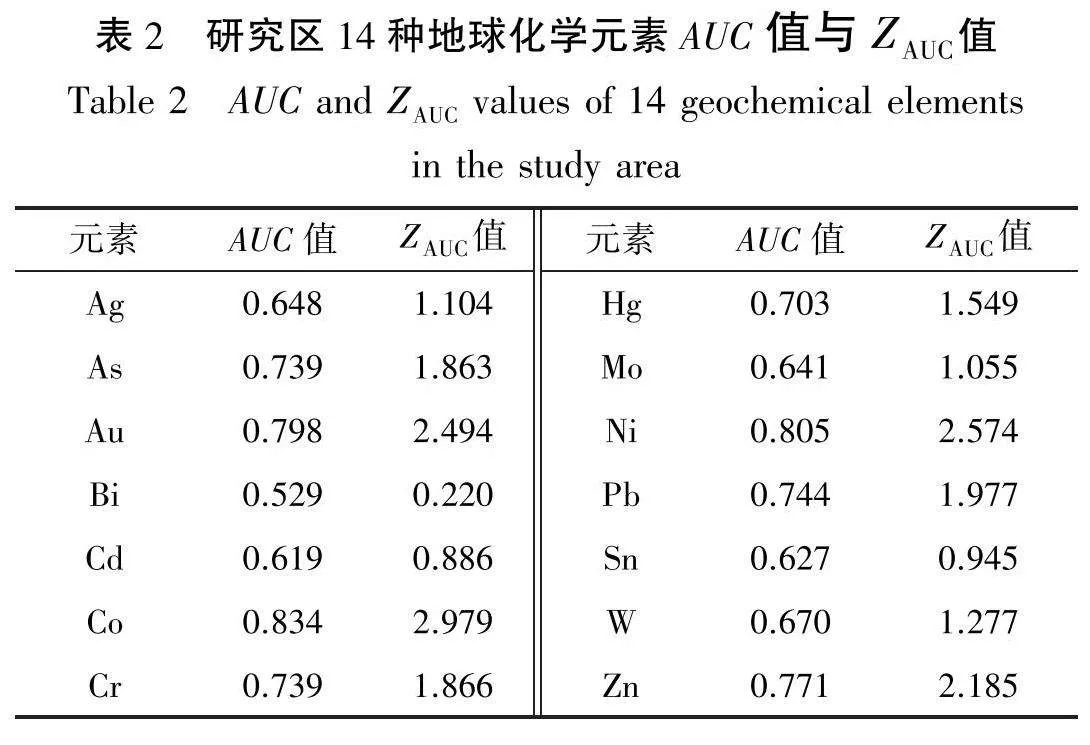
许多元素在空间的浓度分布与特定类型的矿化相关，其有助于指导地质专家发现特定类型矿床[25]。本研究旨在通过分析研究区与金矿化相关的地球化学数据来指导金矿勘查。基于前人研究结果，本文使用ROC（Receiver Operating Characteristic）曲线来评价研究区地球化学模式与已知金矿床（点）位置之间的空间相关性[26-28]。结合ROC曲线下面积（AUC）和对应的满足标准正态分布的随机变量值（ZAuc）选择指示研究区金矿化的元素[14-17]。基于14种元素的浓度值及已知矿化点的对应组成元素浓度绘制了ROC曲线，结果见图2;计算了14种元素AUC值和ZAuc值，结果见表2。由图2可知，Au、Co、Ni、Pb和Zn 5种元素的ROC曲线更加接近ROC空间的左上角，表明该5种元素的浓度分布模式与已知金矿床（点）的位置分布具有较强的空间相关性。由表2可知，Au、Co、Ni、Pb和Zn5种元素的AUC值和ZAuc值分别大于0.5和1.96。因此，就AUC值和Zuc值而言，这5种元素与成矿具有正相关关系[25]。本研究选择Au、Co、Ni、Pb和Zn5种元素作为指示研究区金矿化的地球化学元素。

所选5种指示元素的浓度等值线图见图3。由图3可知，除Au分布较为零散外，剩余4种元素大体呈北西向分布，与韧性剪切带展布方向一致，这5种元素的浓度分布与5个已知金矿床（点）的分布有较强的空间相关性。

3基本算法

3.1 SMOTE算法

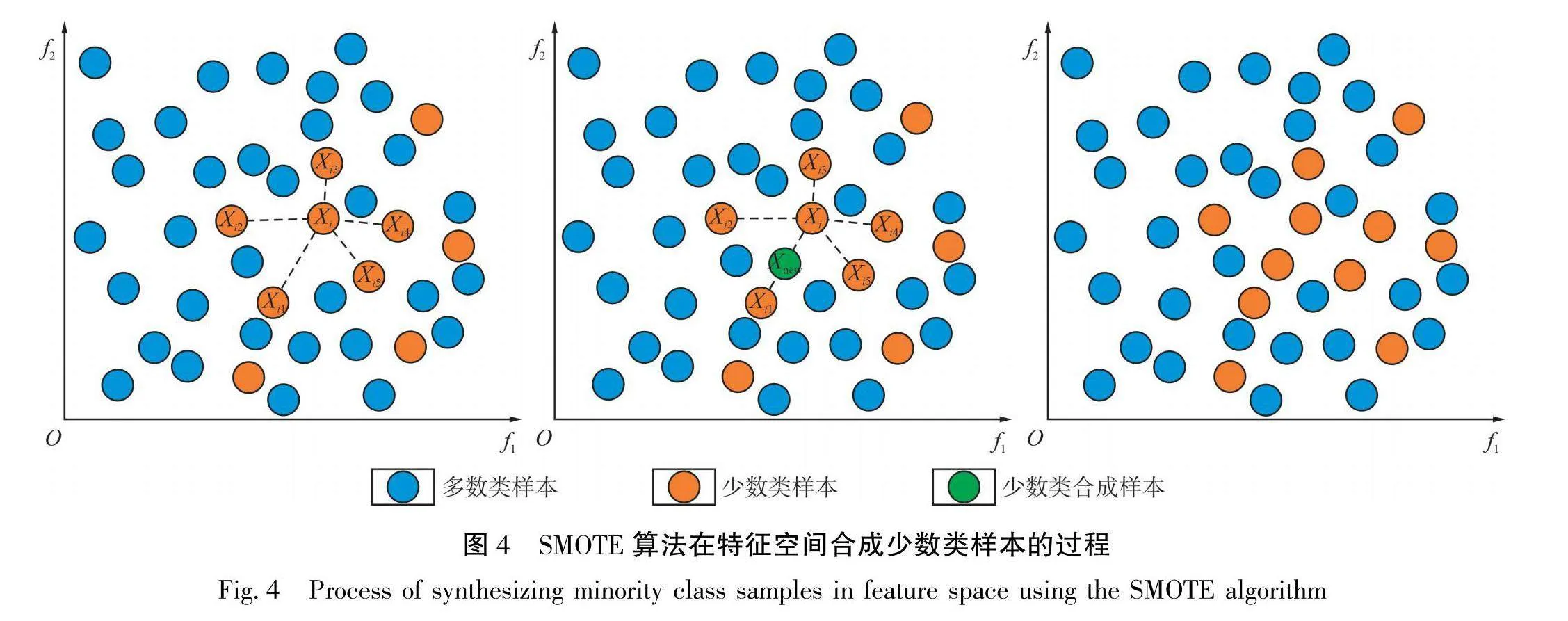
SMOTE算法是由CHAWLA等[18]提出的一种过采样方法，旨在通过数量增强来解决数据的类不平衡问题。该算法受K近邻算法启发，核心思想是对每个少数类样本，在特征空间中使用欧几里得距离来确定其k个最近的同类样本。对于选定的少数类样本及其近邻样本，SMOTE算法通过在它们之间的连线上进行随机插值来合成新的少数类样本。具体而言，对于每个少数类样本x;∈R⁴，首先确定其在同类样本中的k个近邻样本，然后从这k个近邻样本中随机选择1个样本（x，，=1，2，3，…，k）。在样本x₁与x，连接的线段上随机插值生成1个新的样本点xnw。其中，x：，为少数类样本x，的第p个属性值，x，p为近邻样本x.的第p个特征值，p=1，2，3，…，d。新样本xne的第p个特征可通过式（1）计算得出：

式中：λ为介于0和1之间的随机数。

通过上述方法，SMOTE算法创造性地引入新的信息点，增强了数据集中少数类样本的表达。SMOTE算法在特征空间合成少数类样本的过程见图4。

3.2 BRF算法

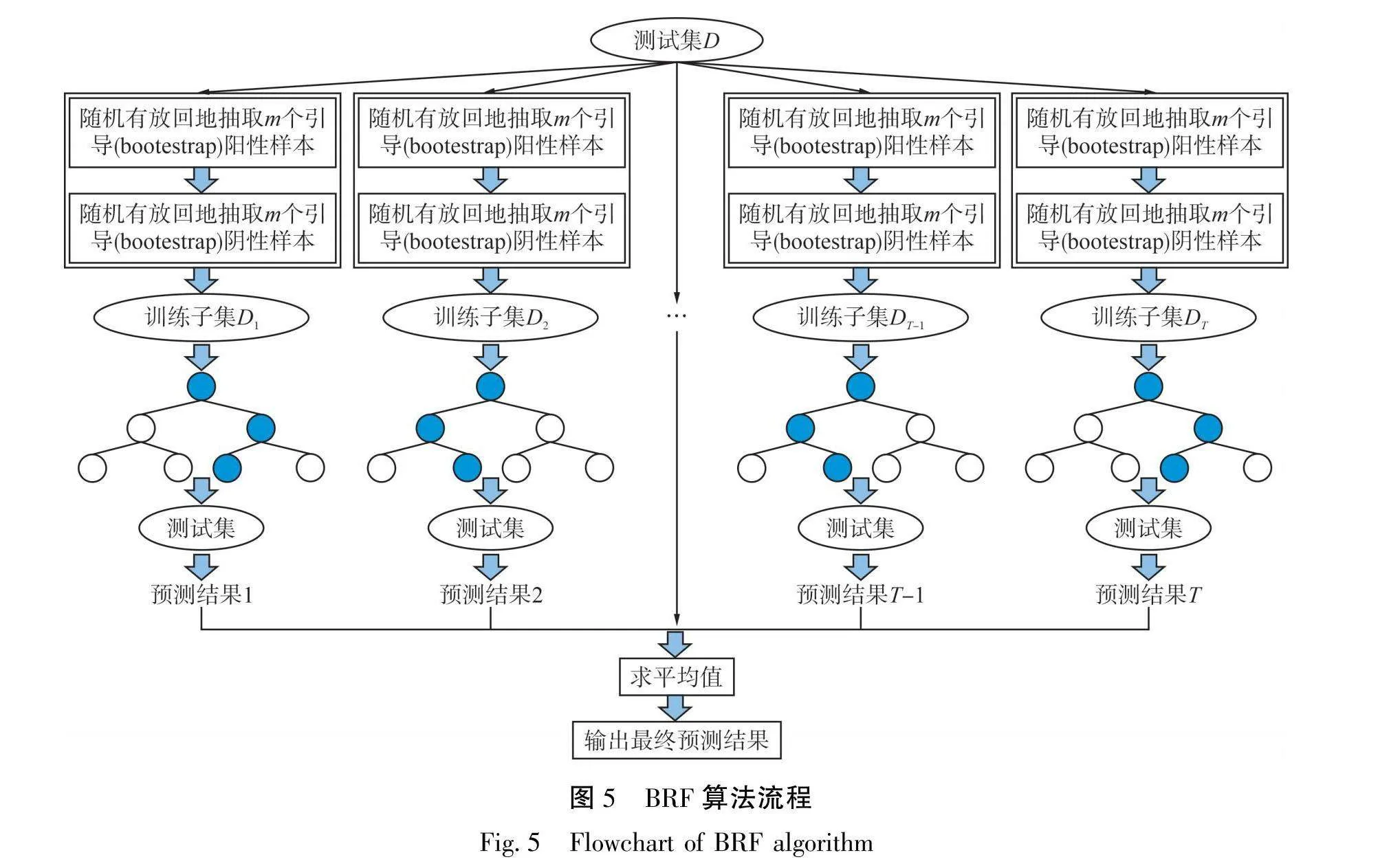
BRF算法是由YOUSRA等[19]提出的一种为了解决训练数据中类不平衡问题而设计的改进RF算法。该算法基于bagging算法的集成思想，同时迭代训练多棵相互独立的决策树（CART）弱分类器，然后使用训练过的每棵决策树对测试集数据进行分类预测并对预测结果通过投票或求平均值的方式进行集成。

在二分类问题中，通常将少数类样本设定为阳性样本，将多数类样本设定为阴性样本。针对二分类问题，给定训练样本集D=（x₁，y₁），（x₂，y₂），（x3，y3），…，（xn，yn）。其中，y，为样本x，的类标签（i=1，2，3，…，n），取0或1（0代表阴性样本，1代表阳性样本），样本集D中阳性样本数量为m;测试集U={x₁，x₂，x3，…，x。;决策树弱分类器迭代次数T，BRF算法的步骤为：

1）对于第t（t=1，2，3，…，T）棵决策树而言，①从训练集的阳性样本中随机有放回地抽取m个引导（bootstrap）样本，同时基于随机欠采样的策略从多数类样本中随机有放回地抽取相同数量的样本；②将抽取相同数量的2类样本组合成一个类平衡的训练子集D，;③从训练子集D，中诱导1棵决策树f，，使其达到指定的最大生长深度，不进行剪枝。

2）将步骤（1）重复多次，直到训练出指定数量（T）的决策树弱分类器。

3）使用T棵训练过的决策树对测试集数据U进行分类预测，令f，（x;）表示第t棵决策树f，预测样本x;（i=1，2，3，…，c）为阳性的概率。

4）对T棵决策树的预测结果通过求平均值得到最终预测结果。其中，T棵决策树对测试样本x;（i=1，2，3，…，c）为阳性样本的概率预测结果表示为：

（2）

上述决策树基于CART算法构建，但进行了部分修改，即在每个节点上不再搜索所有特征变量以获得最佳分割点，而是随机选取部分特征变量进行搜索，有助于增加决策树模型的多样性。BRF算法流程见图5。

4金矿化预测

4.1 SMOTified-BRF模型与BRF模型

为了解决样本中存在的类比平衡问题，首先，使用SMOTE技术对研究区地球化学数据中的5个金矿床（点）样本进行过采样，通过生成一定数量的合成矿化样本，增加了原始地球化学数据集中的已知金矿化样本数量。其次，将包含合成矿化样本的地球化学数据集作为BRF算法的训练集，构建了SMOTified-BRF模型。模型的参数设置对于模型的最终性能具有决定性作用，本研究以模型正确预测已知金矿床（点）的能力作为参数优化指标，使用GridSearchCV进行参数优化。SMOTified-BRF模型的参数设置见表3。训练结束后，将研究区所有样本作为测试数据，使用SMOTified-BRF模型对测试数据进行类别预测。SMOTified-BRF模型输出的是一个向量，表示测试样本属于背景样本的概率与金矿床（点）样本的概率，2类样本的预测概率和为1。同时，使用BRF算法对研究区原始地球化学数据进行建模，构建BRF模型，参数设置与SMOTified-BRF模型的BRF分类器相同。BRF模型输出的是一个向量，表示测试样本属于背景样本的概率与金矿床（点）样本的概率，2类样本的预测概率和为1。

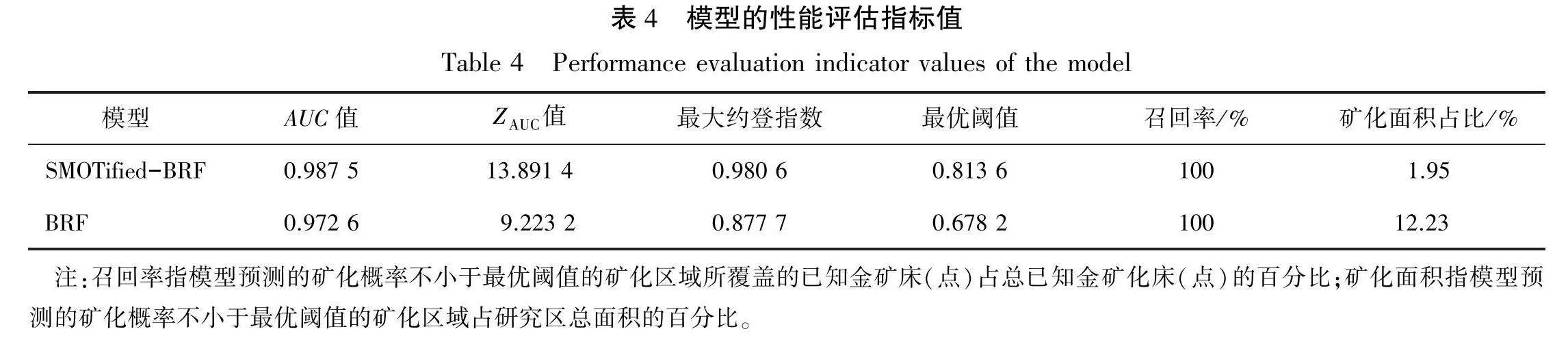
本研究基于SMOTified-BRF模型和BRF模型对研究区地球化学数据进行预测，这2个模型的性能评估指标值见表4。

4.2模型性能评估

ROC常用于评估二分类器的分类性能，已被用于地球化学矿化预测模型的性能评估[15，17，29]。本研究绘制了SMOTified-BRF模型和BRF模型的ROC曲线（见图6）并计算了对应的AUC值和ZAvc值（见表4）。由图6可知，SMOTified-BRF模型的ROC曲线更接近ROC空间的左上角。由表4可知，SMOTi-fied-BRF模型的AUC值为0.9875，高于BRF模型的AUC值（0.9726）。同时，SMOTified-BRF模型（ZAuc=13.8914）和BRF模型（ZAuc=9.2232）的ZAuc值均高于1.96，说明在0.05的显著性水平下，SMOTified-BRF模型和BRF模型的分类性能显著高于随机猜测模型。

4.3矿化区圈定

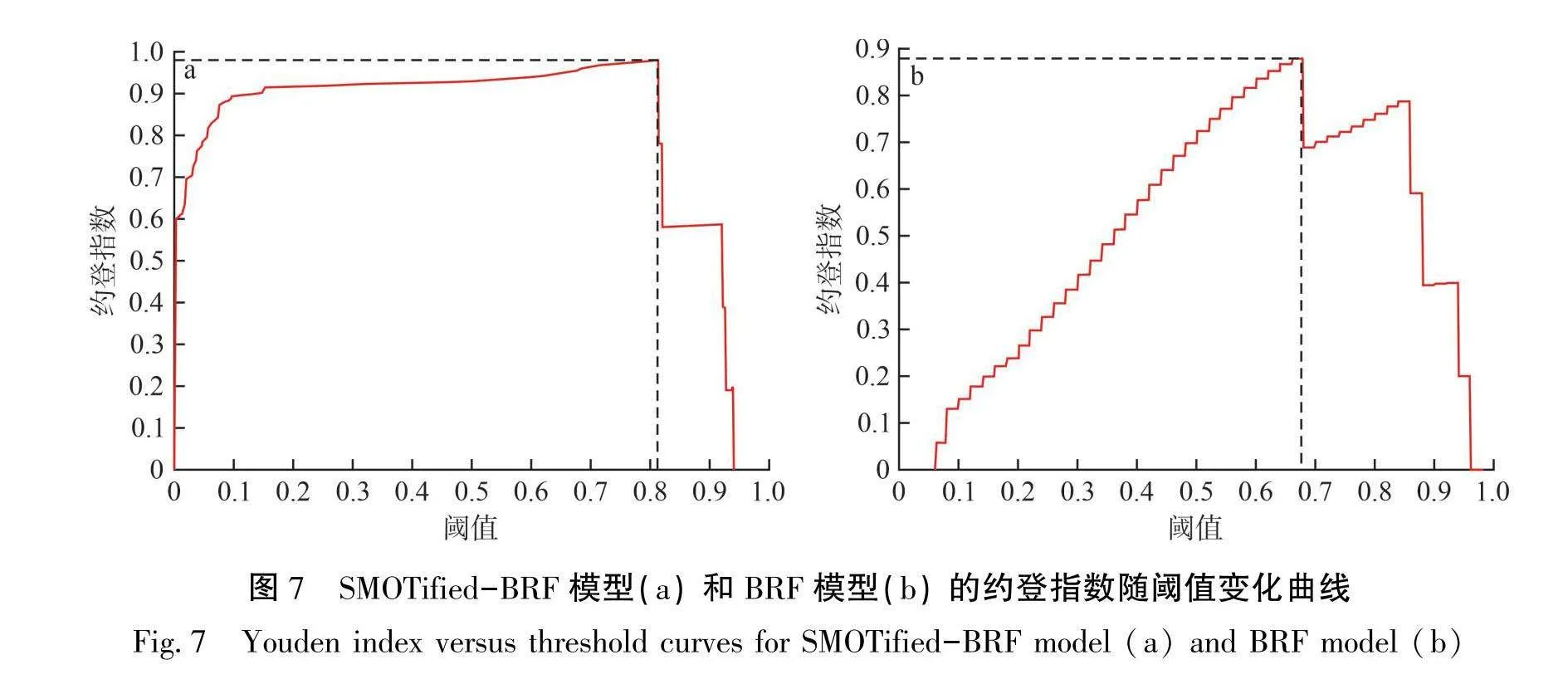
本文引进约登指数（Youden Index，YI）圈定模型预测最优阈值下的研究区金矿化情况[15，29]。约登指数是一种适用于选择最佳分类阈值的统计度量，YI为真阳性率减去假阳性率。在本文中，真阳性率是指所有已知金矿化样本中被模型正确预测出来的已知金矿化样本的比例，假阳性率是指背景样本中被模型预测为已知金矿化样本的比例。约登指数取值为0～1，约登指数值越大，代表模型的分类性能越好。最大约登指数对应的阈值被确定为划分预测矿化区的最优阈值，结果见图7。由图7可知，SMOTified-BRF模型的最大约登指数为0.9806，其对应的最优阈值为0.8136;BRF模型的最大约登指数为0.8777，其对应的最优阈值为0.6782。

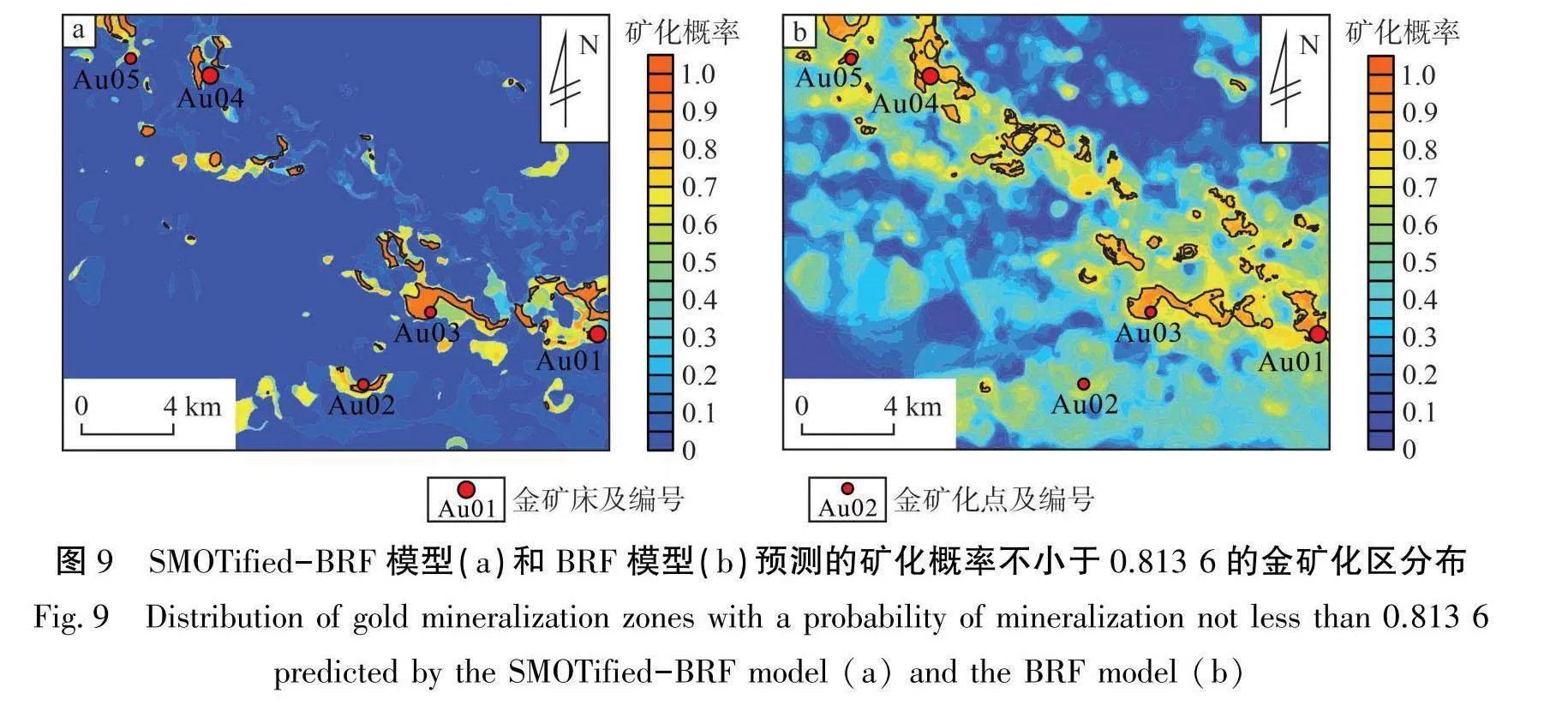
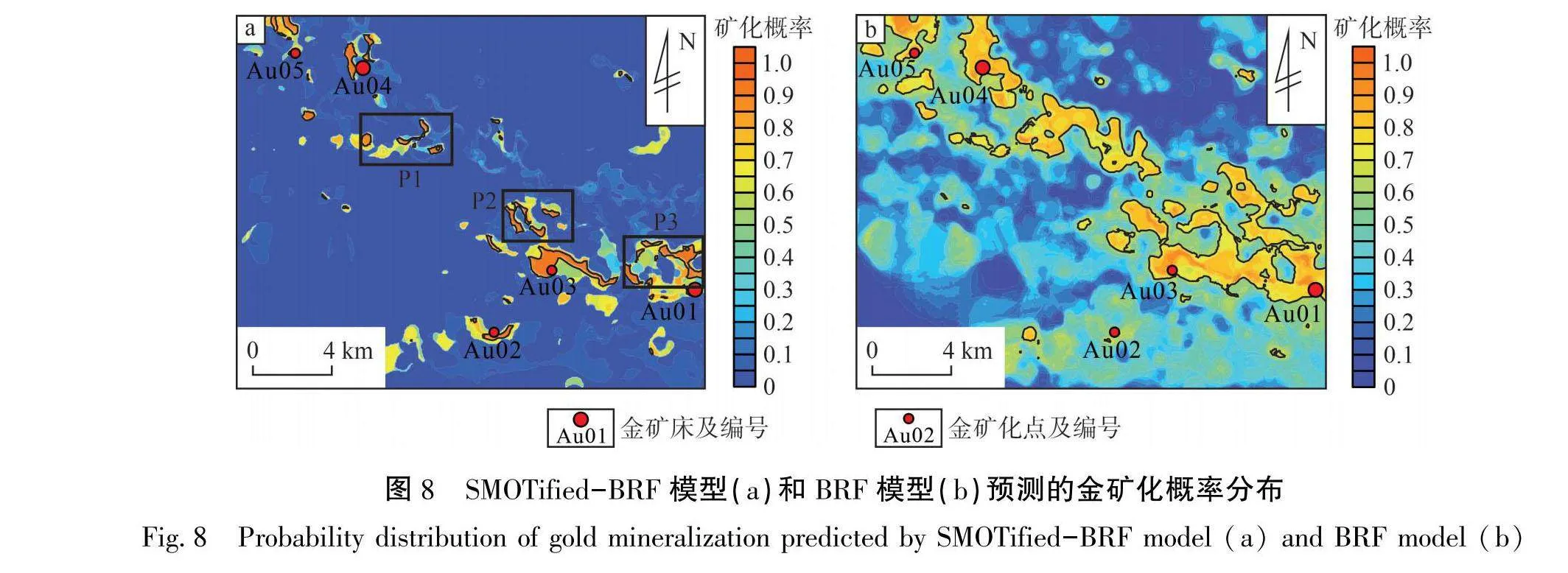
SMOTified-BRF模型和BRF模型预测的金矿化概率分布见图8。基于图7中最高约登指数对应的最优阈值，在图8-a中圈定了金矿化概率大于0.8136的矿化区，在图8-b中圈定了金矿化概率大于0.6782的矿化区。矿化区呈北西向分布，且与已知金矿床（点）的空间分布一致。通过对比图8-a和图8-b可以发现，矿化区覆盖了5个已知金矿床（点）。从圈定面积来看，图8-a圈定的矿化面积占研究区总面积的1.95%，小于图8-b的12.23%。

同时，为避免由于选取不同最优阈值导致的圈定面积差异问题，选取SMOTified-BRF模型的最优阈值0.8136同时作为BRF模型的高矿化概率边界值，预测的矿化概率不小于0.8136的金矿化区分布见图9。由图9可知：SMOTified-BRF模型圈定的矿化区覆盖了5个已知金矿床（点），BRF模型圈定的矿化区仅覆盖了4个已知金矿床（点）;在准确性存在差异的情况下，SMOTified-BRF模型圈定的矿化区面积占比（1.9 5%）仍小于BRF模型中圈定的面积占比（3.96%）。由此可见，SMOTified-BRF模型具有更准确的金矿化相关地球化学金矿化预测性能。

从圈定区域的合理性考虑，图8-a圈定的矿化范围覆盖地层为斑鸠关岩组、洞河岩组、梅子垭岩组；图8-b圈定的矿化范围覆盖地层为斑鸠关岩组、洞河岩组、梅子垭岩组、鲁家坪岩组；图9-b圈定的矿化范围覆盖的地层为斑鸠关岩组、洞河岩组、梅子垭岩组、鲁家坪岩组。从圈定地层与含矿地层情况对比可知，SMOTified-BRF模型和BRF模型所圈定的金矿化预测结果与含矿地层吻合程度较好；从圈定区域与构造的对比情况来看，SMOTified-BRF模型和BRF模型圈定的矿化区整体上沿北西向分布，与韧性剪切带分布一致。以上结果证明，圈定的金矿化预测区具有一定的可靠性。

以SMOTified-BRF模型圈定的金矿化预测区中（见图8-a），除原有金矿床（点）外，另圈定出3处不含已知金矿床（点）的找矿远景区，分别为P1、P2与P3。

找矿远景区P1所处地层为斑鸠关岩组、洞河岩组和鲁家坪岩组，岩性主要为黑色碳质板岩、黑色板岩、绢云石英片岩等，在空间分布上大体沿韧性剪切带分布，且靠近1处石英脉强变形叠加强硅化区界线；找矿远景区P2所处地层为鲁家坪岩组和洞河岩组，岩性主要为绢云石英片岩、黑色板岩等，在空间分布上大体沿韧性剪切带分布，且靠近1处石英脉强变形叠加强硅化区界线；找矿远景区P3所处地层为鲁家坪岩组和洞河岩组，岩性主要为绢云石英片岩、黑色板岩等，在空间分布上，沿韧性剪切带分布，且靠近2处石英脉强变形叠加强硅化区界线。

通过对比地层、岩性、分布及蚀变等情况，圈定的3处找矿远景区具有较好的合理性，可以作为下一步找矿依据。

5结论

1）SMOTified-BRF模型与BRF模型地球化学金矿化预测均能取得较好效果，且预测金矿化区的地层情况与含矿地层一致，分布区域与韧性剪切带吻合，说明具有较好的可靠性，为矿产勘查方面新质生产力的发展提供了新思路。

2）在本次预测中，SMOTified-BRF模型表现优于BRF模型，以AUC值作为评价指标的情况下，SMOTified-BRF模型（0.9875）的表现优于BRF模型（0.9726）;基于约登指数指示的最优阈值的情况下，SMOTified-BRF模型圈定出了更为精确的矿化面积占比（1.95%），相较于BRF模型（12.23%）更为准确。

3）基于SMOTified-BRF模型在汉滨—旬阳地区圈定了3处未包含已知金矿床点的找矿远景区，为进一步找矿提供了新方向。

[参考文献]

[1]习近平主持召开新时代推动东北全面振兴座谈会强调：牢牢把握东北的重要使命奋力谱写东北全面振兴新篇章[N].人民日报，2023-09-10（01）.

[2]杨建锋，余韵，姚晓峰，等.矿产勘查推动新质生产力发展路径初探[J].中国矿业，2024，33（5）：39-45.

[3]王登红.试论稀散金属矿产与新质生产力[J].中国矿业，2024，33（4）：2-12，1.

[4]朱清.发展AI找矿这种新质生产力[N].中国矿业报，2024-03-09.

[5]张七道，肖长源，李致伟，等.黔北普宜地区水系沉积物地球化学特征及成矿预测[J].地质与勘探，2021，57（5）：1040-1052.

[6]安朝，李德彪，柴云，等.青海省东昆仑纳赤台地区正、负异常特征及找矿方向[J].黄金，2019，40（3）：23-29.

[7]张凯伦，温守钦，汪徽，等.辽宁阜新排山楼金矿床深穿透地球化学找矿方法的应用研究[J].黄金，2023，44（9）：111-116.

[8]ZUOR G.Exploration geochemical data mining and weak geochemi-cal anomalies identification[J].Earth Science Frontiers，2019，26（4）：65-75.

[9]zUORG，XIONG YH.Big data analytics of identifying geochemical anomalies supported by machine learning methods[J].Natural Resources Research，2018，27：5-13.

[10]zUO RG，CARRANZA EJ M.Support vector machine：A tool for mapping mineral prospectivity[J].Computers and Geosciences，2011，37：1967-1975.

[11]ABEDI M，NOROUZI GH，BAHROUDI A.Support vector machine for multi-classification of mineral prospectivity areas[J].Computers and Geosciences，2012，46：272-283.

[12]RODRIGUEZ-GALIANO VF，CHICA-OLMO M，CHICA-RIVAS M.Predictive modelling of gold potential with the integration of mul-tisource information based on random forest：A case study on the Rodalquilar Area，Southern Spain[J].International Journal of Geo-graphical Information Science，2014，28：1336-1354.

[13]CARRANZA EJM，LABORTE A G.Random forest predictive modeling of mineral prospectivity with small number of prospects and data with missing values in Abra（Philippines）[J].Computer and Geosciences，2015，74：60-70.

[14]CHEN Y L.Mineral potential mapping with a restricted boltzmann machine[J].0re Geology Reviews，2015，71：749760.

[15]SHAYILAN A，CHEN Y L.A smotified extreme learning machine for identifying mineralization anomalies from geochemical explora-tion data：A case study from the Yeniugou Area，Xinjiang，China[J].Earth Science Informatics，2024，17：1329-1343.

[16]CHEN YL，DUXD，GUO M.Self-paced ensemble for constructing an efficient robust high-performance classification model for detec-ting mineralization anomalies from geochemical exploration data[J]Ore Geology Reviews，2023，157：105418.

[17]GUO M，CHEN Y L.High-performance imbalanced learning ensem-bles of decision trees for detecting mineralization anomalies from geochemical exploration data[J].Journal of Geochemical Explora-tion，2024，259：107443.

[18]CHAWLANV，BOWYER KW，HALLLO，et al.SMOTE：Synthetic minority over-sampling technique[J].Jounal of Artificial Intelli-gence Research，2002，16：321-357

[19]YOUSRA A，AHMAD KM，BASIT R，et al.Predicting influential blogger's by a novel，hybrid and optimized case based reasoning approach with balanced random forest using imbalanced data[J].IEEE Access，2021，9：6836-6854.

[20]姜万录，马歆宇，岳毅，等.类间数据不均衡条件下基于平衡随机森林的轴向柱塞泵故障诊断方法[J].液压与气动，2022，46（3）：45-54.

[21]胡学敏，曾晟，宋良灵.基于灰狼算法改进随机森林算法的爆破振动速度预测研究[J].黄金，2024，45（1）：12-16.

[22]廖华.陕西旬阳烂木沟金矿控矿构造与矿床成因[D].北京：中国地质大学（北京），2020.

[23]许锋，李卫波，宋公社，等.陕西石泉—旬阳地区金矿床控矿因素与成矿模式[J].矿产勘查，2018，9（1）：70-78.

[24]邹海洋，陈松岭，胡祥昭.陕西旬阳淋湘金矿床成矿机制[J].大地构造与成矿学，1997，21（3）：221-227.

[25]ZUO RG.Selection of an elemen tal association related to minerali-zation using spatial analysis[J].Journal of Geochemical Explora-tion，2018，184：150-157.

[26]CHEN Y L.Mineral potential mapping with a restricted boltzmann machine[J].0re Geology Reviews，2015，71：749-760.

[27]CHEN YL，WU W.Application of one-class support vector machine to quickly identify multivariate anomalies from geochemica exploration data[J].Geochemistry：Exploration，Environment，Analysis，2017，17（3）：231-238.

[28]PARSA M，MAGHSOUDI A，YOUSEFI M.A receiver operating characteristics-based geochemical data fusion technique for targe-ting undiscovered mineral deposits[J].Natural Resources Research，2017，27（1）：15-28.

[29]CHEN YL，AN A.Application of ant colony algorithm to geochemi-cal anomaly detection[J].Journal of Geochemical Exploration，2016，164：75-85.

Research on geochemical gold mineralization anomaly prediction based on theSMOTified-BRF model

—A case study of the Hanbin-Xunyang area，Shaanxi Province

Xu Zhenglin'，Wang Xi¹，Xue Linfu¹，Ran Xiangjin'，Yan Qun¹，Li Yongsheng²，³，Yu Xiaofei²3

（1.College of Earth Sciences，Jilin University;2.Development and Research Center，China Geological Survey;3.Mineral Exploration Technology Guidance Center，Ministry of Natural Resources）

Abstract：Mineral exploration is not only a critical component of new quality productive forces but also a driving force for their development.To address the challenges of sample imbalance caused by the limited number of known mineralization samples and the scarcity of mineralization information in gold mineralization prediction during mineral exploration，this study proposes the SMOTified-BRF model.This model applies the SMOTE method to augment the extremely limited known mineralization samples and employs the balanced random forest（BRF）method for prediction.Using the Hanbin-Xunyang area as the study area，geochemical data from stream sediments were analyzed using the SMOTified-BRF and BRF models and compared the gold mineralization prediction outcome and model performance.The results show that the SMOTified-BRF model achieves a higher AUC value（0.9875）compared to the BRF model（0.9726）.Additionally，at the optimal threshold indicated by the Youden index，the predicted mineralized area ratio of the SMOTified-BRF model（1.95%）is significantly smaller than that of the BRF model（12.23%），demonstrating that the SMOTified-BRF model offers more accurate and efficient performance in predicting gold mineralization anomalies.

Keywords：gold mineralization;anomaly;prediction;balanced random forest;SMOTE;geochemistry;Hanbin-Xunyang area