基于机器学习的自来水设备过滤轴承故障诊断

摘 要：为进一步提高自来水设备过滤轴承故障检测效率，本文将机器学习中的聚类算法应用于轴承故障诊断中，引入最大均值差异技术对故障数据进行预处理，并提出堆叠自动编码器（SAE），从轴承的振动信号中学习和提取特征。试验结果表明，当故障直径为12mm～16mm时，故障识别准确率均＞95%，最大识别准确率为99.56%。当故障直径为16mm时，滚珠故障、内滚道故障和外滚道故障的识别准确率分别为98.02%、98.99%和99.56%，机器学习的平均识别精度为96.75%，随机森林和蚁群算法的平均识别精度分别为89.75%和86%。

关键词：机器学习；自来水设备；轴承故障

中图分类号：TU 991" " " 文献标志码：A

在自来水设备中，轴承是一个关键的零部件，轴承的性能好坏直接影整个机械设备的使用寿命[1]。在自来水设备过滤轴承故障中，内外滚道故障是最常见的故障。故障通常发生在滚珠和滚道间。当滚动体滚道表面与其外径间存在磨损时，会引起一系列振动[2]。因此，必须准确掌握自来水设备过滤轴承的运行状态，及时维护受损部件。目前，工业生产中常用的轴承故障分析方法包括包络谱分析、小波分析和经验模态分解等[3]。王海泉等[4]采用几何方法解决故障检测和隔离问题，并验证所提技术的实用性。但是该方法只适用于离散系统，因此无法广泛推广。随着机器学习技术应用于机械故障诊断[5]，该技术已经取得了较大进展。对自来水设备轴承故障诊断模型进行训练和测试，可以进一步提高其诊断准确率和识别率。基于此，本文将机器学习中的聚类算法应用于轴承故障诊断，引入最大均值差异技术对故障数据进行预处理，并提出堆叠自动编码器（SAE），从轴承的振动信号中学习和提取特征，同时利用故障识别准确率和精度评估轴承故障诊断效果。

1 机器学习模型建立

1.1 机器学习（聚类算法）模型建立

聚类分析是一种无监督学习算法，其目标是将数据空间划分为若干个部分，使每个部分中的数据具有一定相似性，从而达到分类的目的。聚类分析可以从大量的数据中提取故障特征信息[6]，不需要事先给定分类模式。聚类算法是一种反复迭代求解的聚类分析方法，也是一种无监督学习的聚类算法。无监督学习方法利用数据样本相互间存在相似性与非相似性将数据集聚类，更注重分析数据集的特征。将聚类算法设定为2个初始聚类中心，分别取值为3和2，再处理剩余的数据，并对数据进行数据分割、重新定义中心、更新簇中心并计算簇类平均值。最后利用聚类结果进行故障诊断[7]。

假设聚类算法中心具有较高的局部密度，采用高斯函数方式来求解局部密度。自来水设备过滤轴承故障数据点i的局域密度ρi[8]如公式（1）所示。

（1）

式中：dij表示数据点i与数据点j间的距离；dc表示截止距离。

1.2 数据预处理

为避免数据采集过程中可能存在的误差，当搭建自来水设备过滤轴承数据采集平台时，需要将数据分为训练集和测试集，并对数据进行预处理，以降低数据的复杂性。为减少训练集数据量，可以选择最小化的目标函数，以在一定程度上降低计算成本。另外还可以纠正一些不符合标准的数据，包括缺失值、重复值和不符合标准的特征等。例如，某自来水设备中的过滤轴承可能会出现故障，但是在故障数据中却没有该故障。对这种不符合标准的数据进行纠正，可以有效减少模型的训练时间。其中，最简单有效的方法是将所有缺失值补全。

当不同故障源域数据差异较大，并且过滤轴承在实际运行中出现的故障数据多、数据维度较高时，自来水设备过滤轴承故障目标域数据与不同源域数据间会存在不同程度的相关性。因此本文使用最大均值差异技术（MMD）计算故障目标域数据与源域数据间的相关性，并使故障数据降维，提高过滤轴承故障处理效率。目标域数据和源域数据间的最大均值差异（MMD）值越小，其相关性就越大。因此，MMD值越小的源域数据对目标域的影响越大，源域数据的权重也就越高。目标域与源域间的相关性由反演MMD值得到，如公式（2）所示，并利用公式（3）计算每个源域的权重。

（2）

（3）

式中：ri为目标域与源域间的相关性；xsi为源域数据；xt为目标域数据；K为源域的数量；wi为源域的权重。

选出权重较高的源域，并从源域中随机抽取相同比例的样本组成新的源域。假设有4个源域数据，分别为源域数据1、源域数据2、源域数据3和源域数据4。公式（2）和公式（3）用于计算目标域数据和4个源域数据间的权重。假设源域数据4的权重远小于其他源域数据的权重，因此放弃源域数据4。然后随机抽取源域数据1、源域数据2和源域数据3中三分之一的数据，组合成混合工况数据。将混合工况数据作为新的源域来训练本文模型。新的源域数据有利于提取自来水设备过滤轴承故障的共同特征，增加故障数据多样性。此外，当生成新的源域数据时，可以消除与目标域数据差异较大的源域，缓解不同源域间存在较大差异的问题，进一步提高自来水设备过滤轴承故障的识别准确率。

1.3 堆叠式自动编码器（SAE）

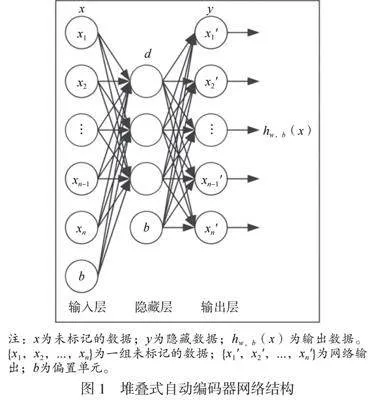
堆叠式自动编码器采用无监督训练方法，可以自主学习数据特征，有效避免人工对故障数据进行分类的问题。堆叠式自动编码器是由编码器堆叠而成的神经网络。该方法基于统计学原理，由自编码器生成一组新的、无关的向量，并训练这些向量，使其能够从原始数据中学习到对原始数据更准确的表示。编码器经过训练和学习来调整网络权重，最终使网络输出等于网络输入。SAE中所使用的损失函数是线性函数，在训练过程中，需要使用学习率、学习速率、正则化因子和优化算法来更新模型参数。堆叠式自动编码器网络结构如图1所示，原始数据从输入层到隐藏层的传输过程称为编码，从隐藏层到输出层的传输过程称为解码。

机器学习模型中的聚类算法对初始中心点十分敏感，如果初始中心点选取不当，会导致整个聚类结果不准确。因此需要控制隐藏层的神经元数量，进一步提高过滤轴承故障特征提取效率，从复杂的过滤轴承输入信号中学习特征信息，并对原始数据进行有效压缩。此时，隐藏层的神经元数量会少于输入层的节点数量。高维原始数据在隐藏层中被压缩，会进一步减轻编码器学习原始数据特征的难度。还可以限制神经元数量，降低轴承故障数据维度。但是网络在隐藏层能学习到的特征较少，在保证隐藏层特征多样性的基础上，本文引入稀疏约束的方法来改进堆叠式自动编码器。其主要思想是限制神经元的活动，降低输入数据的维度。基于机器学习模型的故障检测步骤如下所示。1） 将原始信号导入机器学习算法（聚类算法）中，进行降噪处理和信号重构，再将重构后的信号输入机器学习模型中进行特征提取。2） 利用机器学习模型预测自来水设备过滤轴承故障原始信号，并引入堆叠式自动编码器，得到故障特征值。3） 利用机器学习模型对故障特征值进行训练，将训练好的网络用于过滤轴承的故障诊断。4） 分别测试测试集和诊断集，测试集包括10个不同工况的样本，每个工况样本有4个不同的故障样本。5） 比较不同模型的故障识别性能，选择合适的聚类算法参数。6） 通过多次试验确定聚类算法模型参数。

2 结果与讨论

2.1 试验环境设定

本文数据来自自来水设备过滤轴承数据集。由电机、扭矩传感器和功率测试仪进行数据采集。电机负载为0‌kW～3‌kW，电机转速为1797r/min～1730r/min。过滤轴承振动信号包括正常数据、驱动端加速度数据和基础数据。本文仅采集驱动端故障数据并对其进行分析，采样频率为12kHz。针对内滚道、外滚道和滚动体引入4种不同的故障直径，故障直径分别为10mm、12mm、14mm和16mm。过滤轴承可分为3种故障工况状态，即内滚道故障、滚珠故障和外滚道故障。计算机运行环境配置如下：Intel Core i7-10700 CPU，频率为2.9GHz，RAM为16G，64位Windows10操作系统。自来水设备过滤轴承故障数据采集平台开发采用Python语言。

2.2 故障准确率变化

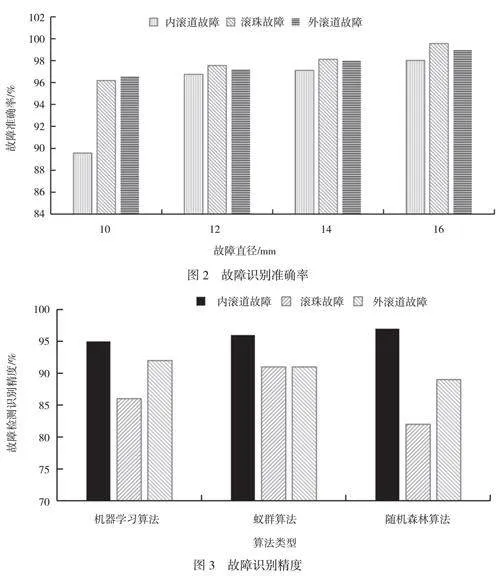
为进一步验证机器学习模型在电机故障诊断中的有效性，本文将自动编码器获得的数据特性发送到softmax分类器进行训练，得到电机轴承的故障类型输出。进而对不同故障工况进行仿真分析，对于每种类型的故障工况，均选择1000组数据作为训练集，200组数据作为测试集。基于机器学习的轴承故障识别准确率如图2所示。

由图2可知，当故障直径为10mm时，内滚道故障的准确率识别较低，准确率仅为89.56%，比滚珠故障、外滚道故障分别下降7.40%、7.24%。主要原因是内滚道发生的故障直径较小，因此故障特征较小，并且内滚道在自来水设备过滤轴承的内部，故障检测难度较大，因此内滚道的故障识别准确率较低。随着故障直径增加，机器学习模型可以识别更多的故障特征，并利用最大均值差异技术缓解不同源域间存在较大差异的问题，提高自来水设备过滤轴承故障的识别准确率。当故障直径为12mm～16mm时，故障识别准确率均＞95%，最大识别准确率为99.56%，说明聚类算法在收敛速度和准确率方面均具有良好效果。当故障直径为16mm时，滚珠故障、内滚道故障和外滚道故障的识别准确率分别为98.02%、98.99%和99.56%。在故障直径相同的条件下，滚珠故障的识别准确率高于内滚道故障与外滚道故障。主要原因是当滚珠发生故障时，其特征较明显，因此识别准确率较高。试验结果表明，本文构建的机器学习模型具有较高的自来水设备过滤轴承故障识别能力。使用该算法对自来水设备过滤轴承进行故障诊断是可行、有效的，能够提高设备运行效率，并降低成本。

2.3 故障识别精度对比变化

机器学习模型具有较好的识别准确率，可准确识别内滚道故障、滚珠故障和外滚道故障。为进一步探究机器学习模型的检测精度，本节将机器学习、蚁群算法和随机森林算法的故障检测精度进行比较，如图3所示。从图3可以看出，机器学习的平均识别精度为96.75%，随机森林和蚁群算法分别为89.75%和86%。在内滚道发生故障的情况下，机器学习的识别精度为95%，蚁群算法和随机森林分别为86%和92%。而当滚珠发生故障时，3个算法模型的识别精度均为91%以上，进一步表明滚珠的故障特征较明显，因此3种算法的识别精度均较高。当外滚道发生故障时，机器学习的识别精度为97%，比蚁群算法和随机森林方法分别提高15.46%和8.25%，蚁群算法和随机森林算法的识别精度低于87%，无法对自来水设备过滤轴承故障进行高效监控。主要原因是机器学习能够利用自编码器生成一组新的、无关的向量，并训练这些向量，使其能够从原始数据中学习到对原始数据更准确的表示。因此，机器学习模型中的聚类算法可用于自来水设备过滤轴承的故障诊断，满足实际设备检测需求。在上述试验中，根据本文提出的故障诊断方法能够对过滤轴承故障进行有效识别，其识别精度为97.84%。在实际应用中，由于时间、人力和精力有限等问题，一般很难准确识别过滤轴承所有状态下的故障，本文所提方法可以在一定程度上减少人工干预，使自来水设备过滤轴承故障诊断结果更客观、准确。而且经过训练学习后的机器学习模型也可以直接应用于其他类型的设备故障诊断中。

3 结论

在相同故障直径条件下，滚珠故障的识别准确率高于内滚道故障和外滚道故障。机器学习模型具有较好的识别准确率，可准确识别内滚道故障、滚珠故障和外滚道故障，其识别精度远高于蚁群算法和随机森林算法，蚁群算法和随机森林算法无法对自来水设备过滤轴承故障进行高效监控。因此，机器学习模型能够用于自来水设备过滤轴承的故障诊断，并满足实际设备检测需求。

参考文献

[1]甄冬，孙赫明，冯国金，等.基于包络谱语义构建的零样本滚动轴承复合故障诊断方法[J].振动与冲击，2024，43（14）：189-200，283.

[2]刘敏，程军圣，谢小平，等.基于改进的辛周期模态分解的滚动轴承复合故障诊断方法[J].振动与冲击，2024，43（14）：47-56.

[3]瞿红春，韩松钰，贾柏谊，等.基于GADF融合RDSAN的跨工况轴承故障诊断[J].组合机床与自动化加工技术，2024（7）：182-187.

[4]王海泉，王亚辉，杨岳毅，等.样本不均衡情况下的航空发动机轴承故障诊断方法[J].郑州航空工业管理学院学报，2024，42（4）：5-11.

[5]彭国良，郑近德，潘海洋，等.集成全息希尔伯特谱分析及其在滚动轴承故障诊断中的应用[J].振动与冲击，2024，43（13）：98-105，125.

[6]胡文浩，吴金龙，董建林.基于混合域特征优选的电机轴承故障诊断[J].机械工程与自动化，2024（4）：32-35.

[7]甄冬，孙赫明，冯国金，等.基于包络谱语义构建的零样本滚动轴承复合故障诊断方法[J].振动与冲击，2024，43（14）：189-200，283.

[8]刘敏，程军圣，谢小平，等.基于改进的辛周期模态分解的滚动轴承复合故障诊断方法[J].振动与冲击，2024，43（14）：47-56.