基于模糊数学的线上课堂教学质量评估指标体系应用研究

2025-01-20丁小星侯帅付芯萌

高教学刊 2025年37期

摘"要：为使军队院校线上教学质量评估指标体系体现实用性和区分性，与“发展性+审核性”教学评价理念相适宜，引入模糊数学判定规则对该体系进一步升级完善，得到评价等级判定算法。该算法基于最大隶属度原则，通过组织测评，计算模糊矩阵，确定指标隶属度向量生成受评对象各项指标等级和对应得分，并通过实例验证其可行性。算法结论与直接判分对比更能客观反映教员现实授课水平和教职发展阶段，从而成为提升线上教学质量的依据和抓手。

关键词：教学评估；评价理念；模糊数学；判定规则；隶属度

中图分类号：G640"""文献标志码：A"""""文章编号：2096-000X（2025）S1-0095-05

Abstract：InordertomaketheOnlineteachingqualityevaluationindexsystemhavepracticalanddiscriminative，whichsuitablefortheconceptof\"developmentamp;review\"teachingevaluation.FuzzyMathematicsDecisionRuleswhichbytheobserveddata，isusedtoupgradeandimprovethesystem.Thealgorithmbasedontheprincipleofmaximummembership，whichgeneratethelevelsandcorrespondingscoresofvariousindicatorsoftheevaluatedobjectbyorganizingevaluations，calculatingfuzzymatricesanddeterminingmembershipdegreevectorofindicators.Itsfeasibilityisverifiedthroughexamples.Comparewithdirectscoring，algorithmconclusionsmoreobjectivelyreflecttheactualteachinglevelandcareerdevelopmentstageofteachers，whichbecomingthebasisandleverforimprovingthequalityofonlineteaching.

Keywords：teachingevaluation;EvaluationTheory;FuzzyMathematics;judgmentrules;degreeofmembership

文献[1]给出的基于简化层次分析法（AHP）[2]的线上课堂教学质量评估指标体系，为军队院校实施线上教学评估提供了指标依据，经试点实践发现该体系存在结论区分度不足，操作性不强等问题，一定程度限制了其与线下教学质量评估体系“无缝对接”以实现对不同教学场景评估的全覆盖，成为制约该体系推广应用的“瓶颈”，故在该指标体系基础上进一步构建能有效区分教员线上教学能力高低，为教学管理部门提升线上教学质量整体水平提供决策依据的评价等级判定规则显得尤为必要。

关于教学评价指标体系结论的区分度和优良率分布问题一直是教育评估领域研究的重点，近年来不少文献从引入智能算法和数学模型角度探讨改进评价规则。例如，为避免仅凭考试成绩确定学员学习水平，结合D-S证据理论的AHP层次分析法，构建基于各阶段学习数据的决策模型，对综合客观评估学员的总体学习能力和进步程度有显著效果和参考价值[3]。进一步，为分析各主客观因素如教员职称、班级规模、生源素质对教评结果的影响，合理优化评价各方权重比例，将基于关联规则的数据挖掘算法应用于分析数据之间的内在联系，确定提高教学质量的关键因素，是辅助教管部门制定个性化评价标准的前瞻性探索[4]。在线教学评估中，因评价方与受评对象非面对面交流，故评价方的结论常具有一定的模糊性，将结论与犹豫模糊语言概念格规则库进行相似性匹配，进而加权取得最优评价值，不失为一种取得线上评估结果较简洁高效的方法[5]，为本文将模糊数学相关理论应用于线上教学质量评估有启发作用。

本研究立足军校线上教学质量评估聚集备战打仗，适应为战育人的现实需求，利用模糊数学中的最大隶属度原则给出具备区分度的评估等级判定算法，对结合不同专业、课程的线上线下混合式教学质量评估优化具有一定的参考和实用价值。

一"模糊数学在课堂教学评价中的应用简介

模糊数学源于1965年美国控制学专家L.A.Zadeh在期刊InformationandControl上发表的一篇研究模糊现象的论文，其主要思想遵循最大隶属原则，即采用模糊统计法、模糊分布法、模糊综合评价等数学方法构建隶属函数（含模糊矩阵、隶属度向量），通过线性计算得到受评对象的评价等级和综合得分。其中，模糊综合评价法（从多个指标因素对被评价对象隶属等级进行评判[6]）是模糊聚类与决策分析在教学评估中常用的方法。

关于模糊数学理论在课堂教学质量评估中的应用，地方高校2010年起已开始探索。2010年，内蒙古农业大学的付玖春[7]在学生评教体系中构建基于模糊数学的二级评估模式，初步验证了该模式的实用性，但由于未对指标作主成分分析，有一定的信息冗余和主观性，需进一步改进。近些年，将模糊数学模型应用于课程评价的研究也在持续推进，2022年，南京工程学院的陈金山等[8]为解决课程综合评价中的模糊条件问题，构建出用于定量分析课程评价的隶属度矩阵，奠定课程发展性评价的理论基础。同年，针对远程教学中思政课程教学质量评价精度低的问题，陕西国际商贸学院的何磊[9]应用ASP技术结合模糊数学综合评价模型和层次分析法构建出思政课程教评指标体系，对军校开展思政课程专项评价有一定的借鉴意义。军队院校在这方面研究亦同步展开，2010年，原第二炮兵工程学院的刘伯宁等[10]，针对军队院校学员学习生活中的心理负荷问题，构建出基于模糊理论的评估指标体系，通过实例验证了可行性。进一步，2014年，原解放军理工大学的张强等[11]针对军校理论课教评各指标缺乏客观数据支撑，主观判断因素较强的问题，引入网络层次分析法和模糊综合评价法给出一些具体改进措施，为本文思路提供了一定的理论依据。然近年来该理论在新一轮军校教学评价中的应用相对较少，可适当深入研究，服务实战化教学。

二"线上教学质量评估指标体系简述

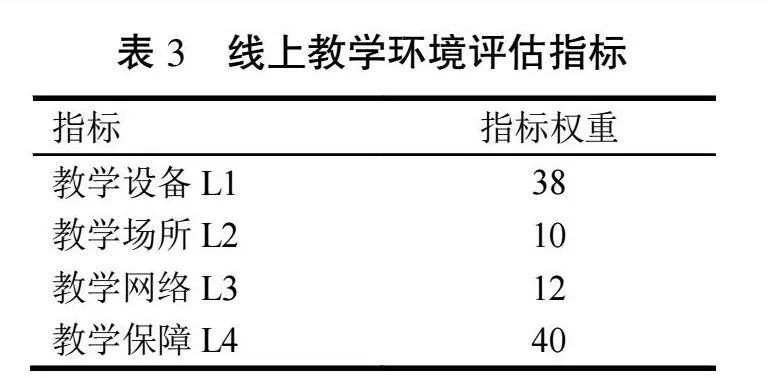
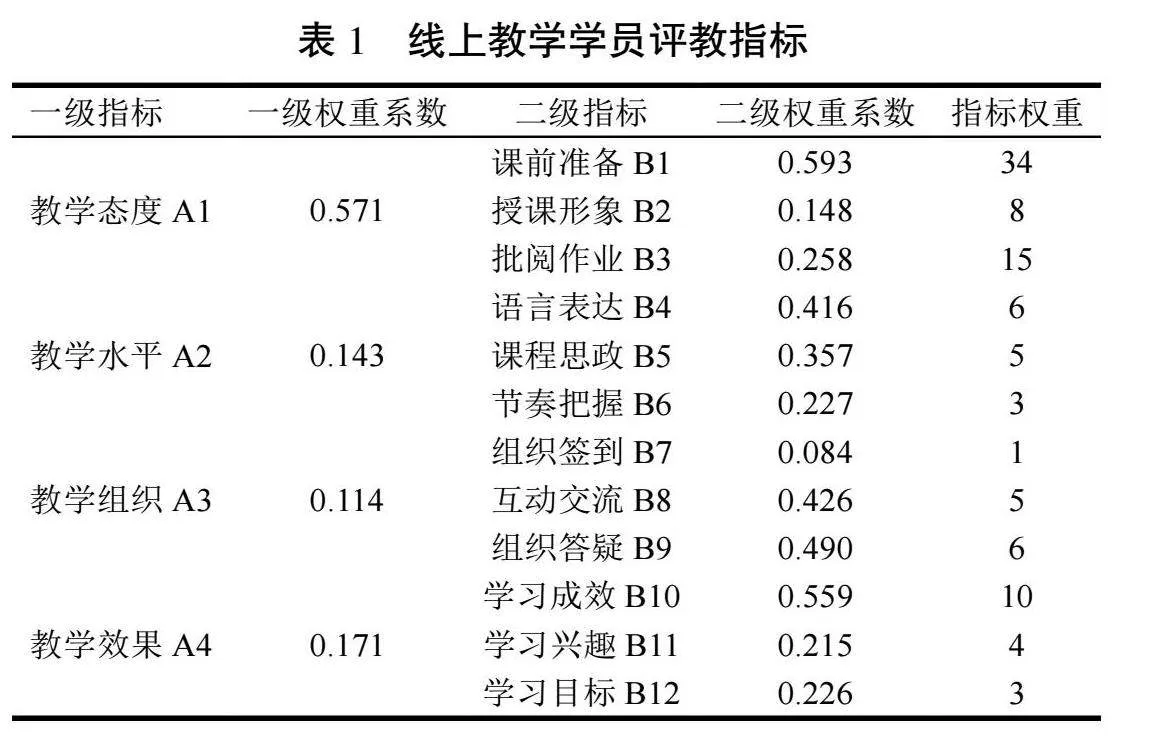
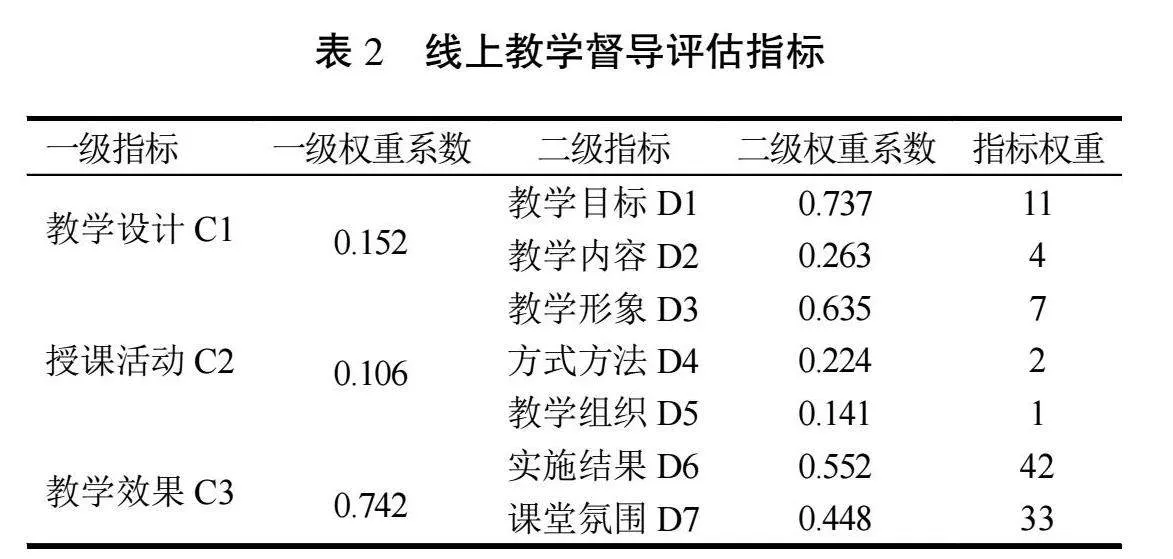
前些年因新冠病毒感染疫情影响，军队和地方院校启动线上教学，与之对应的线上教学评估工作亦同步开展，而线下教学质量评估指标内容不能完全适用于线上教学质量评估，需作修订调整。文献[1]通过问卷调查、专家访谈等形式修订得到线上课堂教学评估指标内容（试行）（涵盖学员评教（表1）、教学督导（表2）、教学环境（表3）等方面，表2、表3指标内容说明详见文献[1]，不再赘述），进一步采用简化的层次分析法（AHP）[2]确定各项指标权重，最终完成线上教学质量评估指标体系构建。

指标内容说明[1]。

课前准备B1：教员课前准备到位，课件、视频等资源利于开展线上教学活动。

授课形象B2：教员线上授课的言谈举止和精神风貌符合学员心目中的教员形象。

批阅作业B3：教员课后认真批阅上传的作业、测验，按时回复学员问题留言。

语言表达B4：教员讲课内容准确，语言简洁、生动，重难点突出，善于对解决问题的方法进行归纳总结。

课程思政B5：教员理论功底扎实、能结合部队实际授课，课程思政明显。

节奏把握B6：教员能注意课堂反馈，有效把握课堂节奏、进度。

组织签到B7：教员课前组织学员签到。

互动交流B8：教员能利用钉钉软件、腾讯会议（非涉密课程）、内网平台（涉密课程）等多种方式组织与学员交流活动。

组织答疑B9：教员结课前及时布置作业，定期组织线上测验和辅导答疑。

学习成效B10：通过线上教学，学员能基本掌握课程内容，学习成效与线下基本一致。

学习兴趣B11：学员在线学习兴趣浓厚，自主学习意识增强，能紧跟教学进度。

学习目标B12：学员在线作业、测验完成率与准确率达到人才培养方案要求。

三"基于模糊数学的线上教学质量评估等级判定算法

本节将第1节介绍的模糊数学判定思路应用于第2节简述的线上教学质量评估指标体系，从而得到线上教学质量评估等级判定算法，算法基本步骤如下。

（一）"组织测评

组织测评人员按评判等级V=[？淄1，？淄２，？淄３，？淄４，？淄５]（注：？淄１为优秀（90分以上），？淄２为良好（80～90分），？淄３为中等（70～80分），？淄４为合格（60～70分），？淄５为不合格（60分以下）），对受评对象的每项二级指标给出评级。

（二）"计算二级指标模糊矩阵

统计每项二级指标统计不同等级的测评人数，计算其与总测评人数的比值，作为该层的模糊矩阵Ｒt（t=1，…，n）的元素。

（三）"计算二级指标判断向量

基于判断向量与模糊矩阵的关系Ｃt=Wt×Rt（Wt为二级指标权重系数，t=1，…，n），计算二级指标层的判断向量Ｃt。

（四）"计算一级指标隶属度向量

二级指标判断向量构成一级指标模糊矩阵Ｇ＝[C1…Ｃn]T，重复执行第3步，得到一级指标隶属度向量B=■×G（■为一级指标权重系数）。

（五）"输出受评对象各一级指标评价等级和综合得分

各一级指标评价等级由P=G·ＶＴＴ＝？琢1，…，？琢n（？琢t值范围为？淄1至？淄5）确定，根据最大隶属度原则，综合得分由F=B×VT得出，通常一级指标隶属度向量B中数值最大元素对应等级即为该教员评价等级。

四"线上教学质量评估等级判定算法的应用

本节将第3节的线上教学质量评估等级判定算法应用于测评某军队院校某学年第一学期线上教学质量。

测评样本：某教学区队（合班）学员200名，教员8名，院（系）督导员10名，教保人员3人。

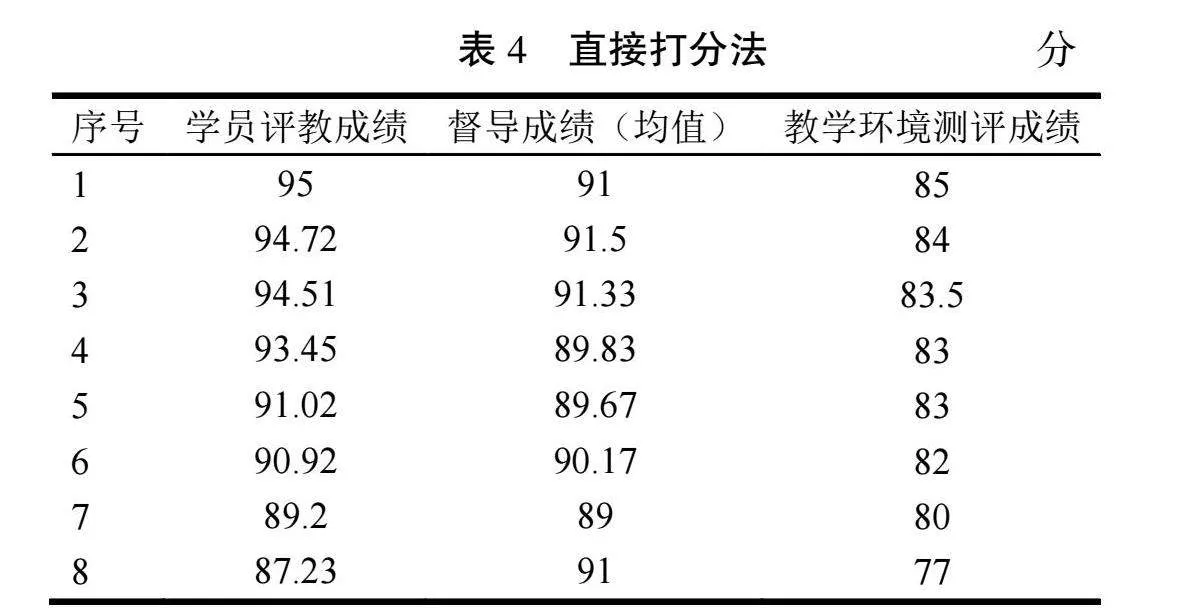
方法一：直接打分。应用第2节简述的线上教学质量评估指标体系[1]对该学期的教员教情（指标调用表1）、教学督导（指标调用表2）、教学环境（指标调用表3）直接打分测评，结论见表4。

结论分析：与线下教学评估结论类似，教员的学员评教成绩、督导成绩以及他们对教学环境测评成绩均比较接近。其中，学员评教成绩90分以上（优秀）占比75%，80分到89分（良好）占比25%，没有中等及以下情形，区分度较低，未能客观反应教员实际授课水平。

方法二：应用第3节线上教学质量评估等级判定算法评级。以测评样本中的学员评教和教学督导为例详述（指标调用表1、表2），其他情况类似。

（一）"指标集向量化

表1一级指标向量U=[A1，A2，A3，A4]，一级系数=[0.571，0.143，0.114，0.171]；二级指标向量集如下：

A1=[B1，B2，B3]，二级系数W1=[0.593，0.148，0.258]A2=[B4，B5，B6]，二级系数W2=[0.416，0.357，0.227]；A3=[B7，B8，B9]，二级系数W3=[0.084，0.426，0.490]；A4=[B10，B11，B12]，二级系数W4=[0.559，0.215，0.226]。

（二）"统计各等级评价人数

统计200名学员（S=200）对某教员二级指标五个等级V=[？淄1，？淄２，？淄３，？淄４，？淄５]的评价人数s（i=1，2，3；j=1，…，5；t=1，…，4），见表5。

（三）"计算二级指标模糊矩阵

（四）"计算二级指标判断向量

Ct=Wt×Rt，t=1，…，4；得到一级指标模糊矩阵G=[C1…Cn]T，其中Ct（t=1，…，4）为二级指标判断向量。

C1=W1×R1=[0.538，0.331，0.089，0.037，0.005]；

C2=W2×R2=[0.481，0.327，0.110，0.070，0.011]；

C3=W3×R3=[0.280，0.284，0.304，0.122，0.009]；

C4=W4×R4=[0.406，0.339，0.188，0.060，0.007]。

（五）"计算一级指标隶属度向量

B=×G=[0.477，0.327，0.134，0.055，0.007]，进而得到各一级指标评价得分（可转化为对应等级）P=（Ｇ·ＶT），综合得分F=B×VT=85.61（注：等级向量V的各元素转化为各等级学员评分的均值V=93.17，83.６５，74.15，63.23，56.41）。

（六）"输出受评对象各一级指标评价等级和综合得分

输出受评对象各一级指标评价等级和综合得分，见表6。

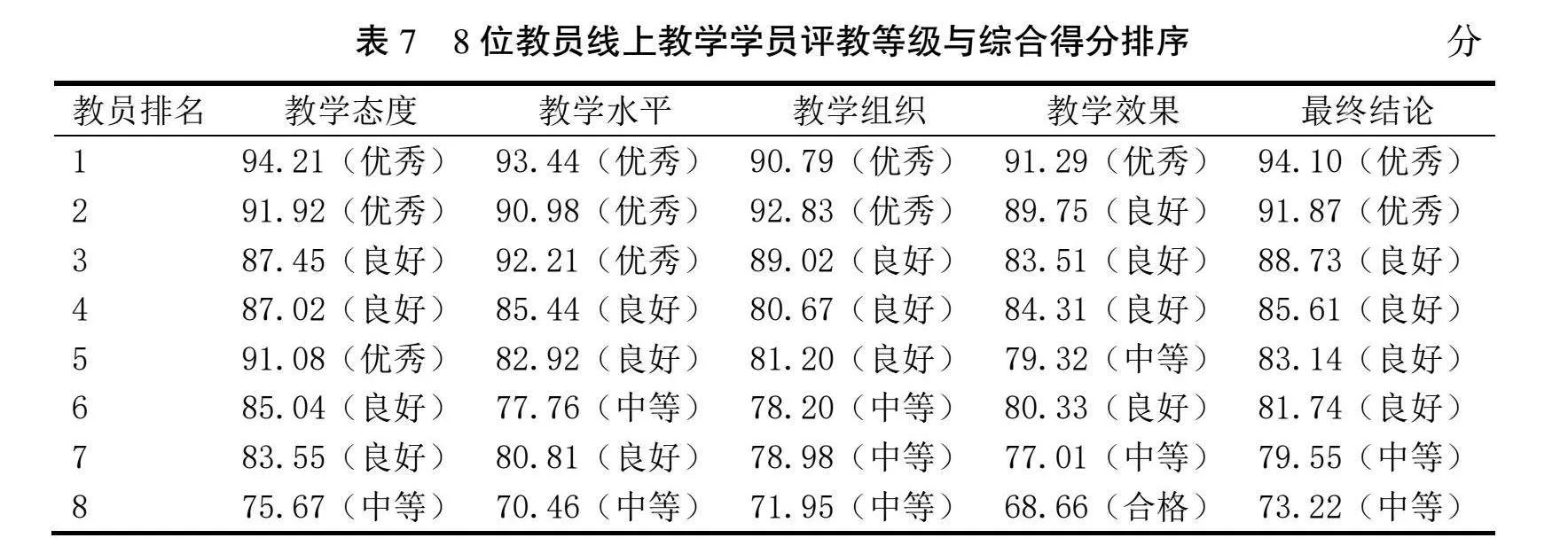
重复执行（一）至（六）步得到该教学区队其他7位教员线上教学学员评教等级与综合得分排序，见表7。

结论分析：按方法二进行测评，由表7可知，学员评教成绩90分以上（优秀）占比25%，80分至89分（良好）占比50%，70分至79分（中等）占比25%，与方法一（表4直接打分法）相比具有一定的区分度，能较客观反映学员对教员线上教学情况的评价。

进一步，在表2指标集向量化的基础上，统计3名督导员（每位教员平均被3名督导员听课）对某教员二级指标五个等级的评价人数s■■（i=1，2，3；j=1，…，5；t=1，2，3），见表8。

再次调用线上教学质量评估等级判定算法，得到二级指标模糊矩阵及对应的判断向量：

R’1=0.6670.333""0""0"0"0""0.6670.333"0"0；

C’1=W’1×R’1=[0.492，0.421，0.088，0，0];

R’２=0.6670.333"0"0"00.3330.667"0"0"0"0"""1""0"0"0；

C’２=W’２×R’２=[0.498，0.502，0，0，0]；

R’3=０"0.667"0.333"0"00""1"""0""0"0；

C’3=W’3×R’3=[0，0.816，0.184，0，0]。

式中：W’1=[0.737，0.263]，W’2=[0.635，0.224，0.141]，W’3=[0.552，0.448]为二级指标向量，一级指标模糊矩阵

。

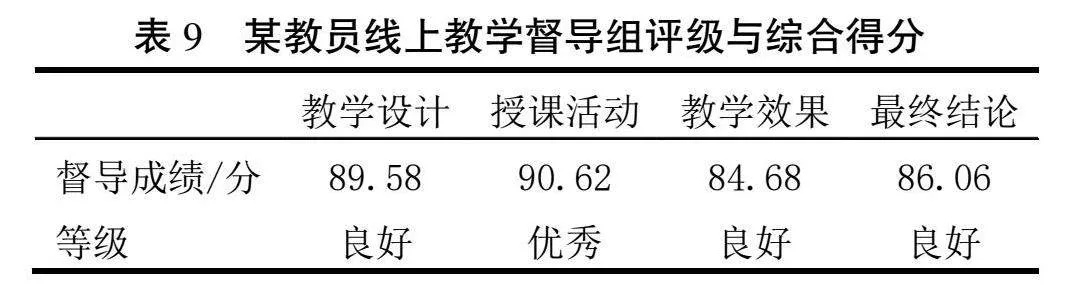
最后，输出受评对象各一级指标评价等级和综合得分，见表9。

其中一级指标隶属度向量B′=′×G′=[0.128，0.723，0.150，0，0]；一级指标评价得分P′=G′·V′＝[８９.５8，９０.６２，84.68]，综合得分F′=B′×V′=86.06（注：′=[0.152，0.106，0.742]为一级指标向量，等级向量V′各元素转化为各等级教学督导组评分均值V′=[94.51，86.75，７５.５，６４.4，55.1]）。

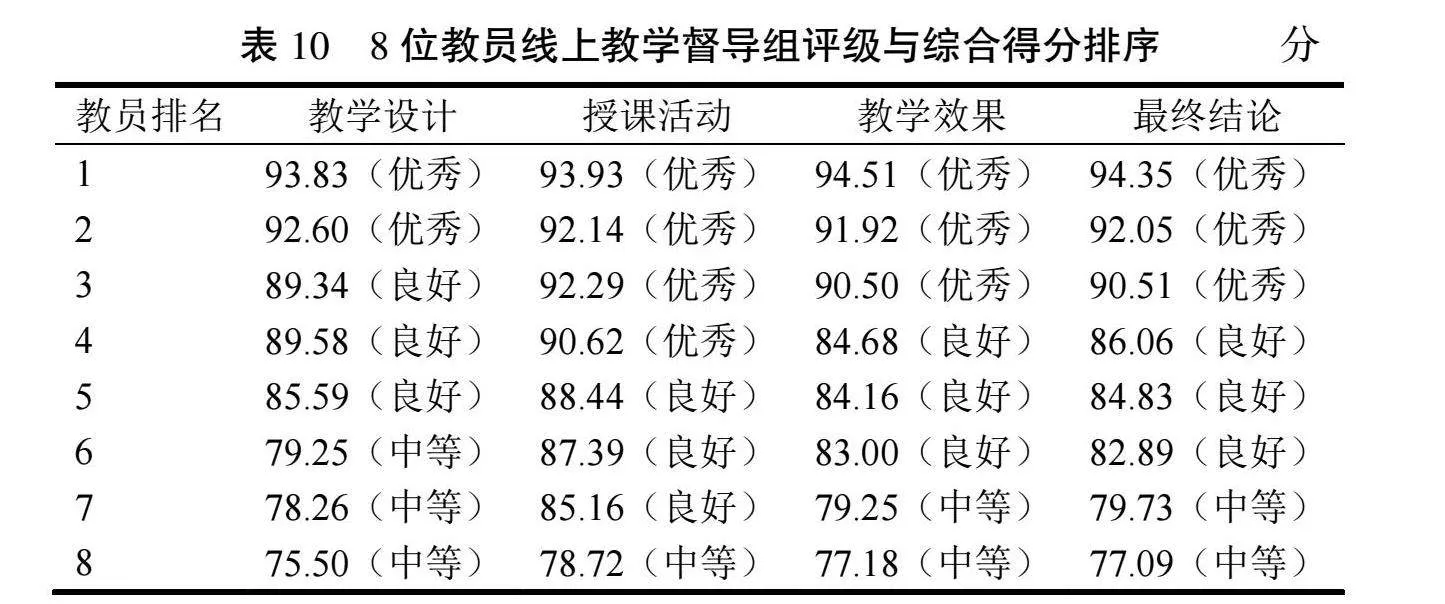
该教学区队其他7位教员线上教学督导组评级与综合得分同理可得，排序后见表10。

结论分析：按方法二进行测评，教员督导成绩最终结论90分以上（优秀）占比37.5%（低于方法一（表4）62.5%）；80分至89分（良好）占比37.5%（与方法一持平）；70分至79分（中等）占比25%（高于方法一0%）。亦说明方法二能客观反映督导专家对教员线上授课水平的评价，但因每位教员的督导评级仅由3位督导员给出，样本量较学员评教少（学员评教人数200人），且督导员评级时，主要集中于优秀、良好两级，区分度仍有改善余地。

五"结束语

本文立足实现线上课堂教学质量评估指标体系的区分性和可操作性，应用模糊数学评价模式给出线上教学质量评估等级判定算法，通过实例分析验证算法可行性，一定程度解决该指标体系在应用方面的“堵点”，对下步结合不同专业、课程的线上线下混合式教学评估优化具有一定的实用意义。

参考文献：

[1]丁小星，侯帅，付芯萌．军队院校线上教学质量评估指标体系探究[J]．高教学刊，2023，9（S2）：52-57.

[2]廖红强，邱勇，杨侠，等．对应用层次分析法确定权重系数的探讨[J]．机械工程师，2012，44（6）：22-25.

[3]马文俊，黄楠，蒋运承，等．基于DS/AHP模型的学生综合成绩评估体系设计——以计算机科学与技术专业为例[J].2019，10（39）：1-4.

[4]祁瑞丽，郭学涛，孟军英，等.数据挖掘技术在高校教学评价中的应用研究[J]．石家庄学院学报，2020，22（3）：65-68.

[5]张烨，刘妍喆，张晓辉，等.基于犹豫模糊语言概念格的在线教学评价方法[J].2023，22（2）：154-158.

[6]谢季坚，刘承平.模糊数学方法及其应用（第四版）[M]．武汉：华中科技大学出版社，2013，93-100.

[7]付玖春．模糊数学在学生网上评教体系中的应用[J]．内蒙古农业大学学报（社会科学版），2010，129（1）：138-140.

[8]陈金山，李振红，庄卫国，等．基于模糊数学原理的课程评价持续改进[J]．中国冶金教育，2022，31（6）：24-29.

[9]何磊．基于模糊数学综合评价法的高校思政课程远程教学系统质量评价[J]．微型电脑应用，2022，38（6）：69-78.