滇东北地区滑坡易发性评价

摘要：在研究滇东北地震滑坡危险区滑坡致灾因子和孕灾环境的基础上，选取了地形、地质、其他共3大类12项评价因子，通过评价因子独立性检验，构建滑坡易发性评价指标体系。随机选取研究区70%的滑坡点作为滑坡易发性评价训练样本，运用GIS空间分析功能，分别采用确定性系数模型、二元逻辑回归模型以及二者组成的耦合模型进行滑坡易发性评价。选取未参与训练样本的30%滑坡点作为检验样本，使用受试者工作特征（ROC）曲线对以上3种模型的评价结果和精度进行验证。结果显示：高程、坡度、距道路距离、地质岩性、NDVI、年平均降雨量对滑坡易发性影响相对较大。耦合模型的AUC值为0.781，高于确定性系数模型的AUC值0.754和二元逻辑回归模型的AUC值0.748。耦合模型合理性和评价精度高于单一模型，且均符合模型检验要求。耦合模型揭示了各评价因子对滑坡易发性影响的差异性，能够较好地反映滑坡易发性影响因子之间相互权重大小，预测的研究区滑坡的空间分布与野外实际调查结果高度吻合。

关键词：滇东北；滑坡；易发性；耦合模型

中图分类号：P315.94"" 文献标识码：A"" 文章编号：1000-0666（2025）01-0089-11

doi：10.20015/j.cnki.ISSN1000-0666.2025.0010

0 引言

滑坡是一种常见的地质灾害，在山区广泛发育，易造成生命财产损失和生命线工程破坏。滇东北地震滑坡危险区包括会泽县、昭阳区、鲁甸县、巧家县、永善县、彝良县、大关县。危险区活动断层发育、地质环境脆弱、地震活动频发，曾发生过多次中强地震。近年来，人类活动对自然环境的干扰破坏力度逐渐增大，在原生环境和次生环境的双重影响下，该地区历史地震滑坡失稳复活、降雨滑坡频繁发生，给居民生命财产安全和生存环境造成了严重威胁，制约了当地经济社会的可持续发展。因此对该地区开展滑坡易发性评价研究，实现科学准确预测研究区滑坡发生的空间分布显得尤为重要。

滑坡易发性评价是指对特定区域内多个影响因子组合导致滑坡发生的可能性评估（罗路广等，2021），是滑坡危险性和风险性评价的基础，是灾区恢复重建和灾害风险治理的重要工具。常见的滑坡易发性评价有基于力学模型与数理统计模型两种。基于力学模型是基于物体力学平衡原理建立的，侧重震后地震滑坡影响要素分析和易发性评价，适用于发震构造清楚或地震动记录完整的情况（林高聪等，2021）。数理统计模型主要依赖经验模型进行滑坡预测，侧重对现有滑坡与其影响因子的分析统计，常用的数理统计模型有确定性系数模型（Certainty Factor，CF）、判别分析法模型、信息量模型、逻辑回归模型（Logistic Regression，LR）等。

近年国内一些学者利用一系列数理统计模型对滇东北地区进行了滑坡易发性研究，均取得了一定的应用效果，如雷林洋（2017）采用证据权模型和地震危险指数模型，对盐津县滑坡易发性和危险性进行了研究；杨德旭（2019）应用二元逻辑回归模型，对巧家县地震滑坡发生概率进行了空间预测。然而，以上研究仅基于统计学模型中的一种模型对滇东北地区的部分县区进行了滑坡易发性评估，缺乏对不同模型结果的对比。单一模型评估还存在滑坡易发性评价因子的量化、各评价因子之间以及同一评价因子不同特征值之间对滑坡易发性的影响值确定的人为因素干扰等缺陷。相比单一模型，耦合模型在合理性、评价精度与成功率方面具有显著的优越性（罗路广等，2021）。

因此，本文采用确定性系数模型、二元逻辑回归模型及二者组成的耦合模型开展滇东北地震滑坡危险区滑坡易发性评价研究，以期实现研究区滑坡发生活动强度以及危害大小的可能性空间预测。

1 研究区概况

滇东北地震滑坡危险区属高山峡谷地貌，面积约20 231 km2，地势南高北低，发育有小江断裂、马边—大关断裂、则木河断裂、昭通—鲁甸断裂。区内地震活动频繁，有历史地震记录以来该区内共发生MS≥5.0破坏性地震22次，其中MS6.0～6.9地震3次，MS5.0～5.9地震19次。

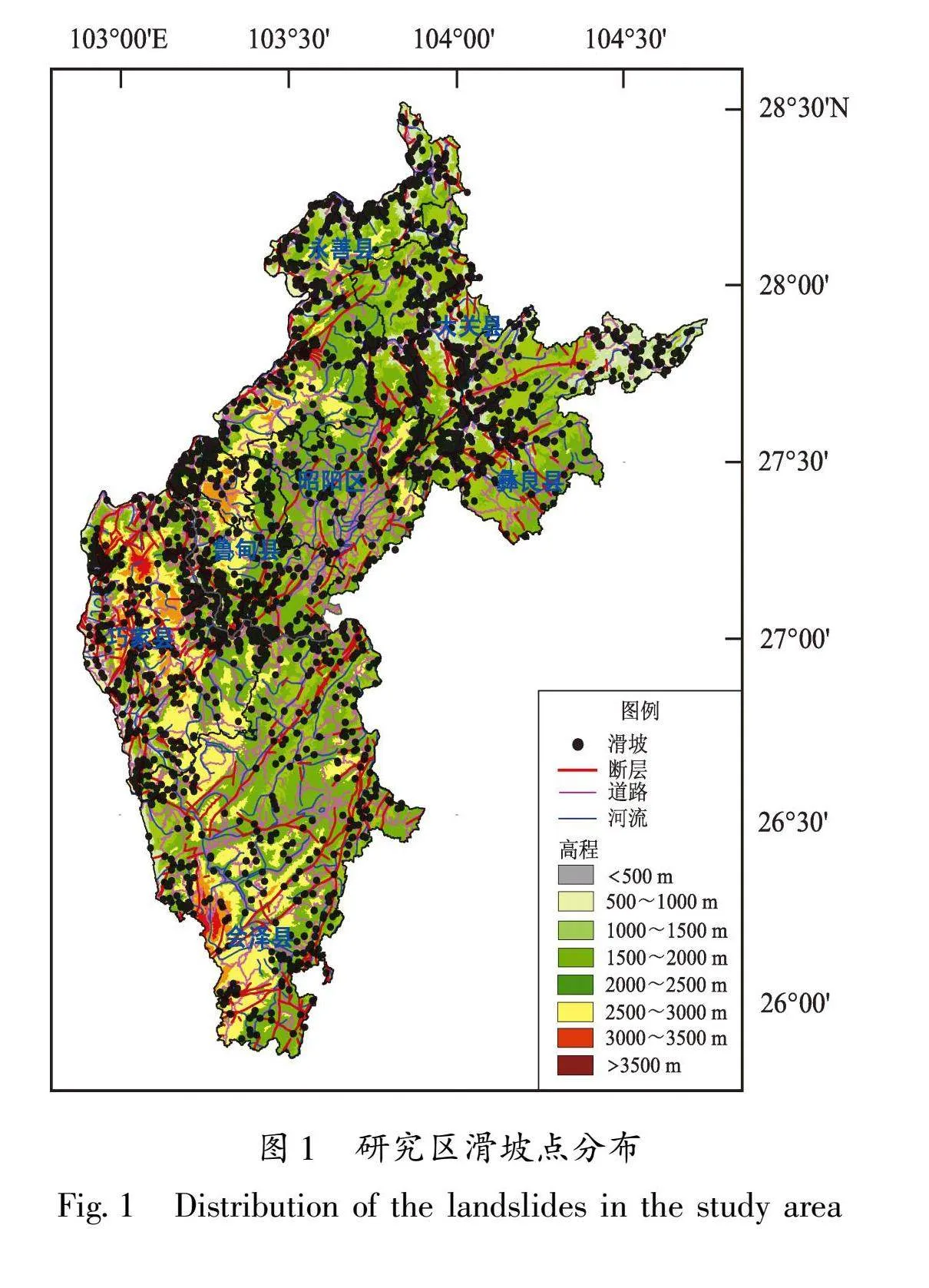
研究区主要发育有滑坡、崩塌、泥石流、地面塌陷等地质灾害，其中滑坡最为频发，主要分布于研究区北部、中部高海拔、活动断层、河流以及道路发育较为密集区域（图1）。

2 研究方法

2.1 数据来源与预处理

滑坡易发性评价研究所需的基础数据主要来源于统计、规划与遥感。其中滑坡数据来源于自然资源局，通过野外实际调查和遥感影像对比修正，数据具有较强的时效性和可靠性。数据来源与详情见表1。利用ArcGIS软件将评价因子坐标统一为WGS_1984_UTM_Zone_48N，并将所有矢量化格式的影响因子以30 m×30 m的分辨率进行栅格化处理。

2.2 技术路线

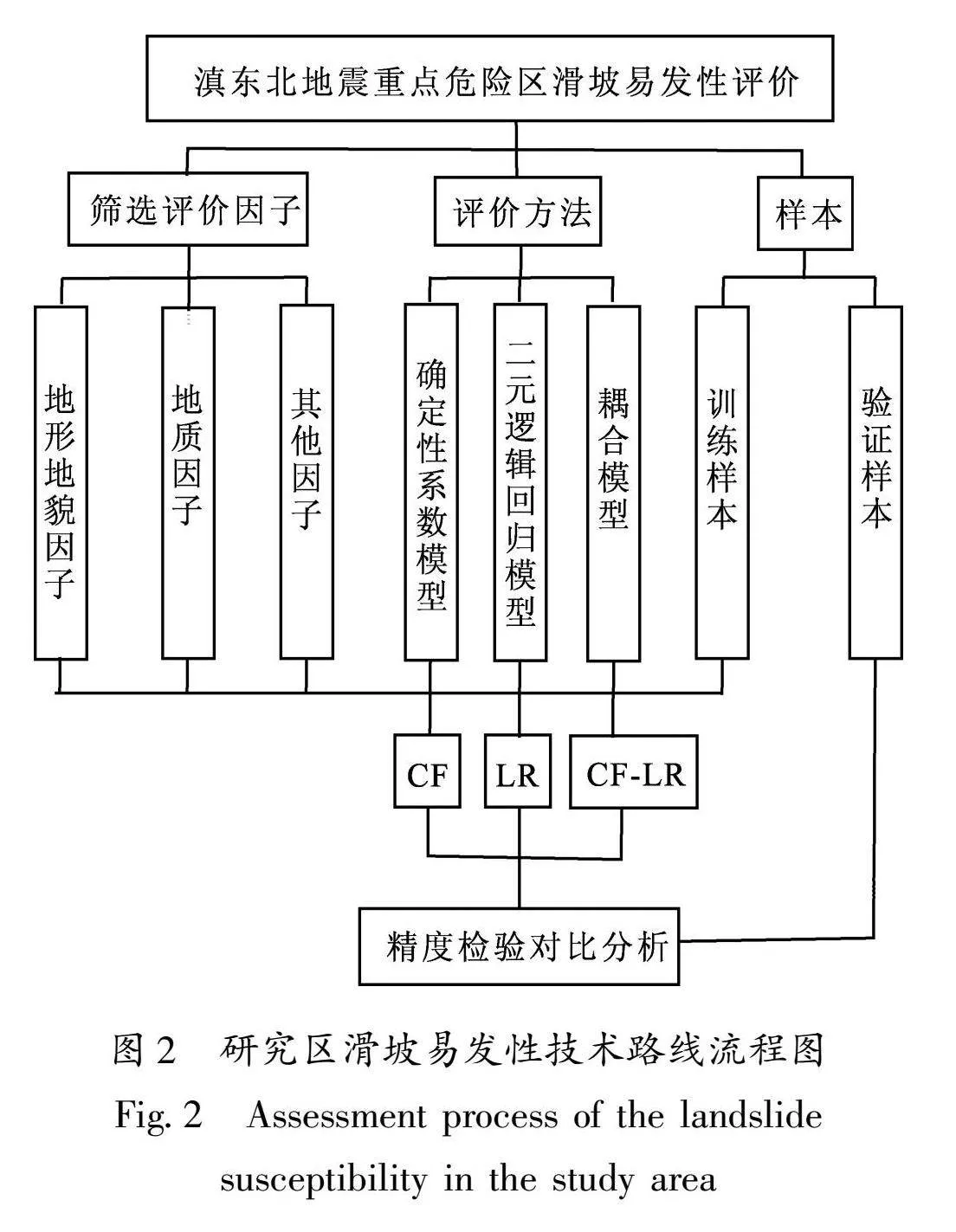
本文选取30 m×30 m的栅格单元开展滑坡易发性评价，选取研究区内的2 481个滑坡点作为滑坡样本，在滑坡样本点100 m的缓冲区外利用GIS随机抽样，提取2 481个非滑坡样本，与滑坡样本组成总样本，按7∶3的比例，将总样本中3 474个样本点作为训练样本集，剩余的1 488个样本点作为检验样本。通过GIS空间分析，以滑坡个数、点密度和确定性系数为统计指标，得出研究区滑坡在不同评价因子下的分布特征和空间分布规律。利用确定性系数模型、二元逻辑回归模型及二者组成的耦合模型对研究区的滑坡易发性进行评价，并利用受试者工作曲线（ROC曲线）对模型评价结果进行检验。最终实现研究区滑坡发生可能性空间概率预测，技术路线如图2所示。

2.3 评价模型

2.3.1 确定性系数模型

确定性系数模型是由Shortliffe 和Buchanan（1975）提出用来表示概率的函数，Heckerman（1986）对该模型进行了完善。该模型评价流程简单，预测准确度较高，被广泛应用于地质灾害易发性评价。计算公式为：

CF=Pa-PsPs（1-Pa）"" （Palt;Ps）

Pa-PsPa（1-Ps）" "（Pa≥Ps）（1）

式中：CF为确定性系数值，区间为［-1，1］，当CF值为0～1时，CF值越接近于1，代表滑坡发生可能性越高；CF值为0～-1时，CF值越接近于-1，滑坡发生的可能性越低；CF值为0时不确定滑坡是否发生（张晓东等，2018）。Pa为滑坡在因子分级类别a中发生的条件概率，以滑坡在分类级别a中的个数与分类级别a面积的比值表示；Ps为滑坡在整个研究区的发生概率，即研究区滑坡总个数与研究区总面积的比值。

2.3.2 二元逻辑回归模型

二元逻辑回归模型是二项分类因变量常用的统计分析模型，表示二元因变量和独立变量的关系。在滑坡易发性评价中，它描述的是因变量滑坡是否发生（0代表不发生，1代表发生）和多个致灾因子之间的关系（罗路广等，2021），计算公式为：

P=11+e-yy=α+β1X1+…+βnXn（2）

式中：P表示滑坡发生的概率，范围为［0，1］，值越大表示滑坡发生的可能性越高；y为滑坡发生的可能性与各评价因子（X1，X2，X3，…，Xn）之间的关系；α、βn分别为二元逻辑回归模型计算出的一个常数项和各评价因子的回归系数。

2.3.3 耦合模型

将确定性系数模型与二元逻辑回归模型进行耦合，解决不同评价因子对滑坡易发性影响的差异性，以提高滑坡易发性评价精度。利用确定性系数模型得到各评价因子分类级别的CF值，用二元逻辑回归模型运算得到各评价因子的回归系数，引入回归系数（因子权重）将评价因子的CF值进行加权，得到耦合模型滑坡易发性指数，计算公式如下：

I=∑ni=1WiIi=∑ni=1WiCFi（i=1，2，…，n）（3）

2.4 评价因子分析

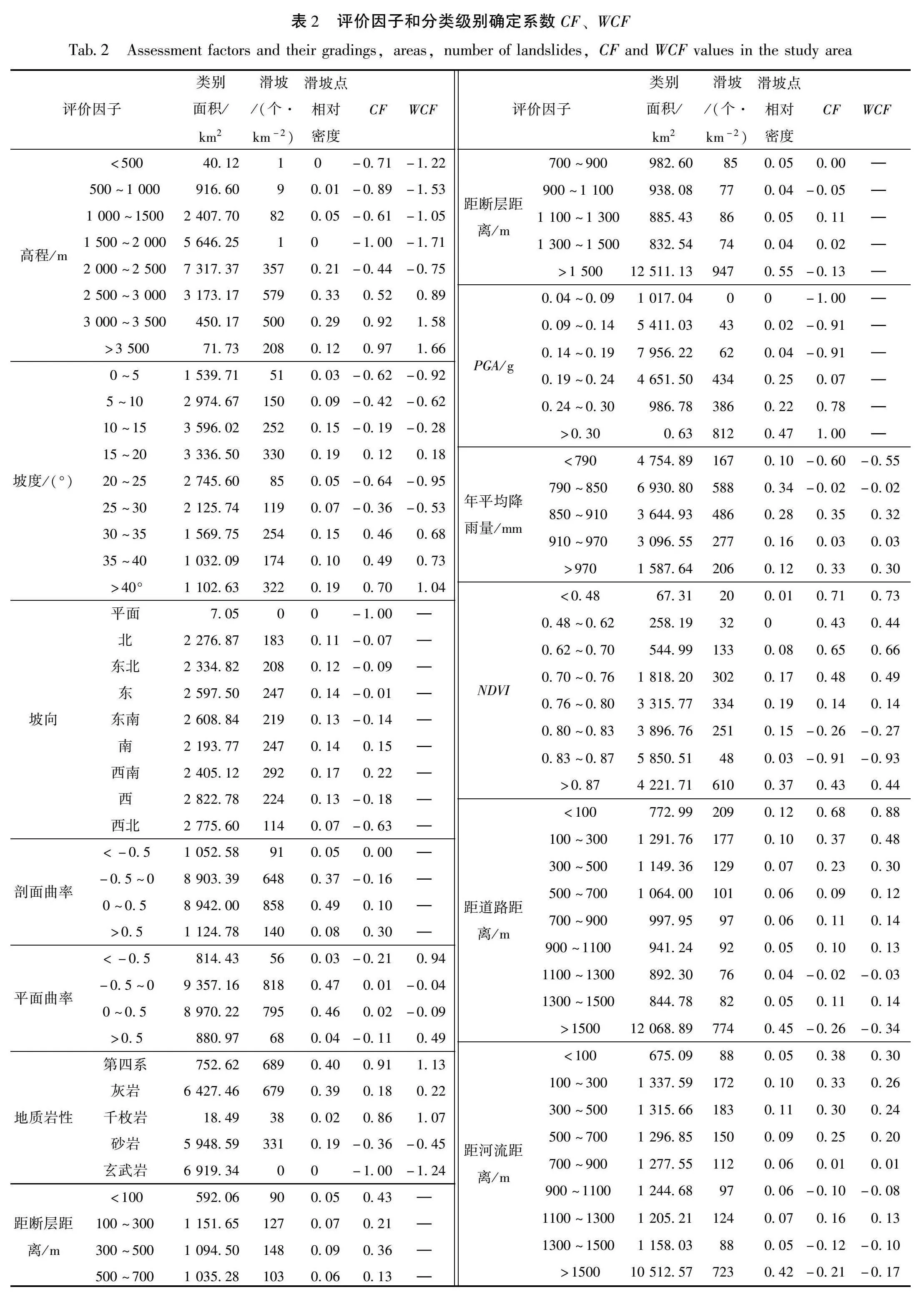
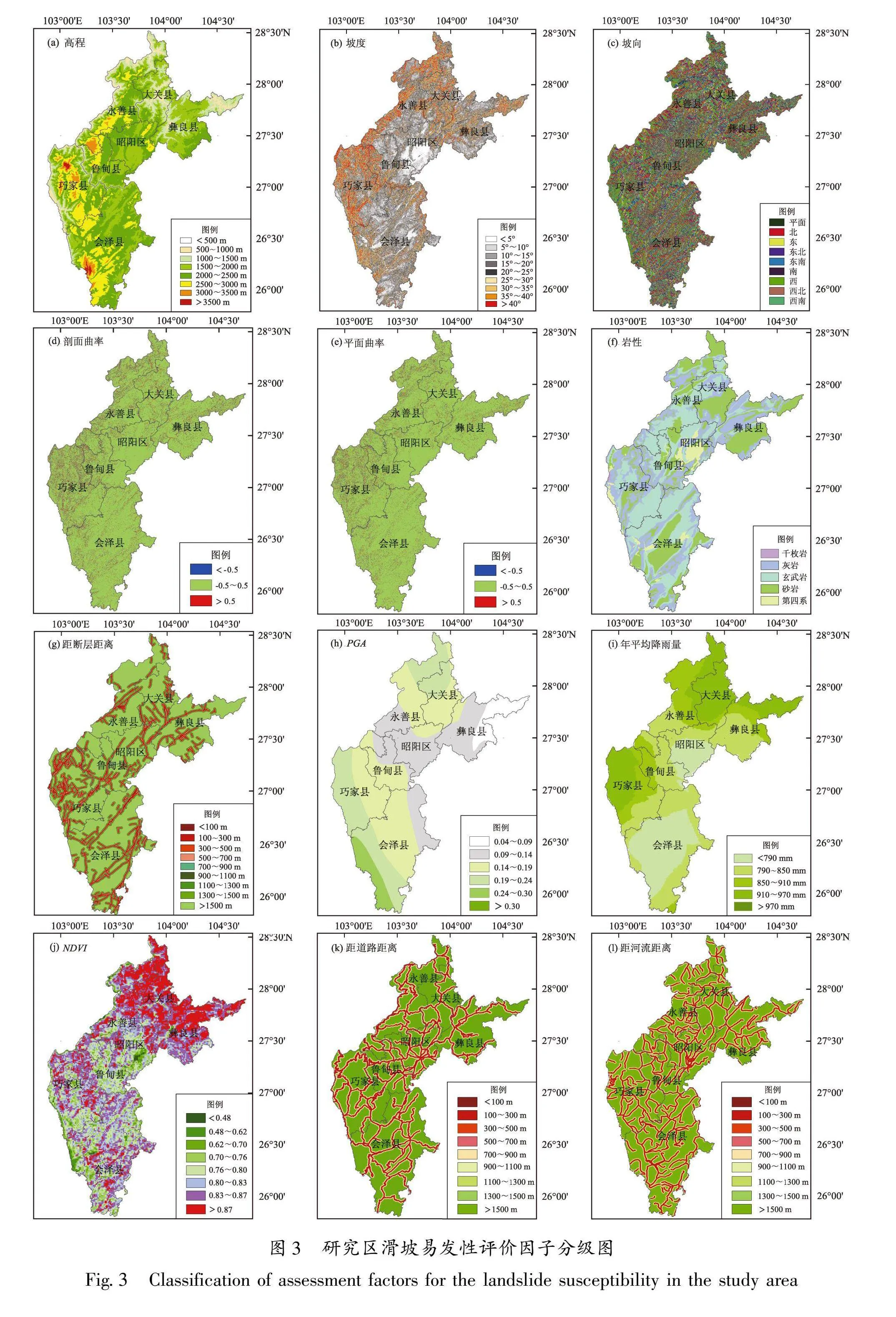
滑坡发生与否由滑坡内部物质基础与外部环境因素共同作用决定。基于前人研究成果、研究区所处地质构造背景和现场实际地质调查，选取地形地貌、地质、其他共3大类12个评价因子，统计各评价因子各分类级别面积、滑坡数量、确定性系数CF值（表2），分析讨论各评价因子分类级别对滑坡易发性的影响（图3）。

2.4.1 地形地貌因子

地形地貌是影响滑坡发育的重要因数（汪旭涛等，2013）。通过研究区DEM数据提取到坡度、坡向、剖面曲率、平面曲率。

（1）高程：高程影响着滑坡体势能、气候分布与植被覆盖率、人类工程活动等因素。研究区滑坡个数与滑坡点相对密度在高程为2 500～3000 m和3 000～3 500 m时最大；CF值在高程大于1 500 m时，随着高程的增加而增大，说明高程对滑坡发育有着正向作用。

（2）坡度：坡度控制着滑坡的应力条件、移动方向、滑坡体的稳定性，提供了滑坡发生的临空面（刘丽娜等，2014）。在坡度大于20°时，滑坡个数、CF值与坡度呈正相关性，当坡度gt;40°时，CF值达最大值0.70，表明坡度易于滑坡的发生。

（3）坡向：不同坡向滑坡的光照时长、植被覆盖度、土壤湿度存在差异，这些差异影响着滑坡体的物理力学特性（张俊等，2016）。滑坡个数、滑坡点相对密度与CF值在西南、南向最大，说明研究区阳坡面比阴坡面更利于滑坡的发生。

（4）剖面曲率：剖面曲率反映了坡度表面某一点的扭曲变化程度，其值为负表示斜坡为凹坡，为正值表示斜坡为凸坡，为0或接近0表示坡面平坦。滑坡个数、滑坡点相对密度与CF值在剖面曲率为0～0.5时最大，且CF值与剖面曲率呈正相关，表明剖面曲率为正值对滑坡发生有正向作用。

（5）平面曲率：平面曲率的正值与负值分别表示地表径流发散和收敛。滑坡个数、滑坡点相对密度与CF值在平面曲率为-0.5～0.5时最大。

2.4.2 地质因子

（1）地层岩性：地层岩性是滑坡体的物源基础。滑坡个数在第四系松散堆积物、灰岩和砂岩中分布最多，滑坡点相对密度和CF值在第四系松散堆积物中最大，表明滑坡体岩性为第四系松散堆积物时，滑坡体稳定性较差，易发生滑坡。

（2）距断层距离：区域断层的错动影响滑坡体节理、裂隙的发育，从而控制着滑坡体的稳定性。滑坡个数、滑坡点相对密度在断层距离大于1 500 m处最大，CF值与断层距离呈负相关，随断层距离的增大而减小，距断层越近越有利于滑坡的发育。

（3）地震动峰值加速度（PGA）：滑坡个数、滑坡点密度与CF值与PGA呈正相关，随PGA的增大而增加，说明PGA越大，越有利于滑坡发育。

2.4.3 其他因子

（1）年平均降雨量：降雨对滑坡体进行冲刷、侵蚀，使滑坡体发生软化或崩解泥化（郭子正等，2020），从而降低滑坡体强度，为滑坡发生提供外动力条件。滑坡个数、滑坡点相对密度在降雨量为790～850 mm时最大；CF值与降雨量整体呈正相关，在降雨量为850～910 mm时最大，表明降雨量对滑坡的发生有一定的影响。

（2）NDVI：植被通过影响降雨量和水系地表径流和滑坡体表层松散沉积物抗侵蚀能力，进而影响滑坡体稳定性。滑坡个数、滑坡点相对密度在NDVIgt;0.87最大，确定性系数CF值与NDVI整体呈负相关，表明研究区NDVI指数越高越不利于滑坡的发育。

（3）距道路距离：道路基础设施建设，通过开挖边坡、切坡，改变了滑坡体的应力状态，增大滑坡临空面，易加剧滑坡的发生。滑坡个数、滑坡点相对密度在距道路距离gt;1 500 m处最大；CF值与道路距离整体呈负相关，随距道路距离的增大而衰减，在距离道路100 m内，CF值最大，表明研究区道路建设易促进滑坡发育。

（4）距河流距离：河流对滑坡的影响在于水系对河流两岸滑坡体的冲刷、侵润和对滑坡体前缘侵蚀作用，导致岸坡形成陡峭的临空面或增加斜坡临空面，从而破坏滑坡体的稳定性。滑坡点个数、滑坡点相对密度在道路距离gt;1 500 m处最大；CF值与道路距离整体呈负相关，在距河流500 m内，CF值最大，说明距离河流越近，越促进滑坡发育。

3 滑坡易发性评价

3.1 评价流程

基于评价因子栅格数据，利用确定性系数模型（式1）得到各评价因子不同分类级别的CF值，将其作为自变量，将是否发生滑坡作为因变量，导入SPSS软件，进行二元逻辑回归分析（式2），得到各评价因子的回归系数即因子之间的权重。基于耦合模型计算得到各评价单元的滑坡加权易发性指数（式3），最终运用自然断点法实现研究区滑坡易发性分区。

3.2 评价因子独立性检验

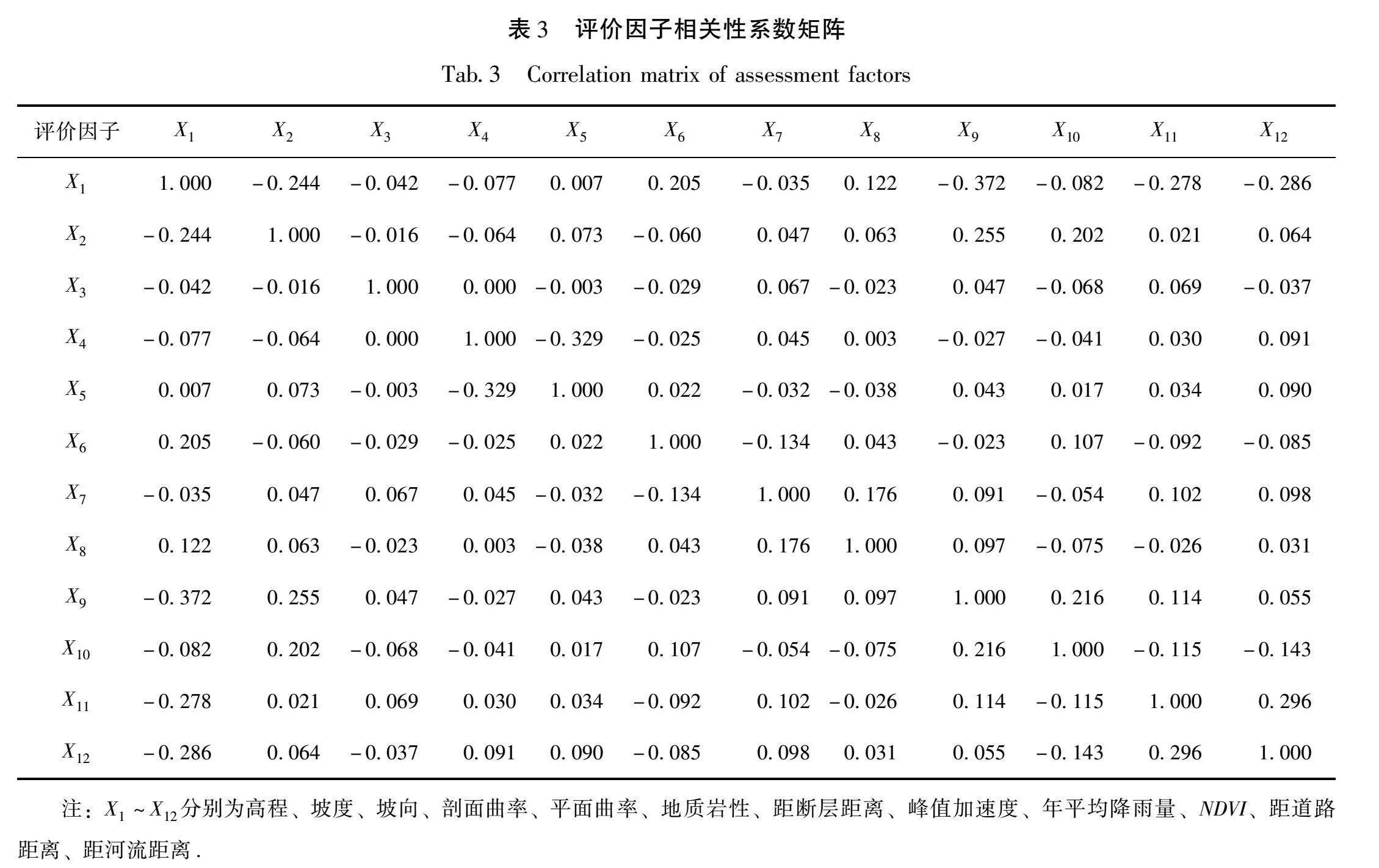
评价因子之间存在相关性会影响滑坡易发性评价模型的准确性。为保证各评价因子满足模型要求，需对各评价因子之间的独立性进行检验，以剔除存在相关性的评价因子。各评价因子的相关系数矩阵见表3。由表3可知，各评价因子之间的相关系数均小于0.3，说明各评价因子之间不存在多重共线性，所有评价因子均可进入模型。

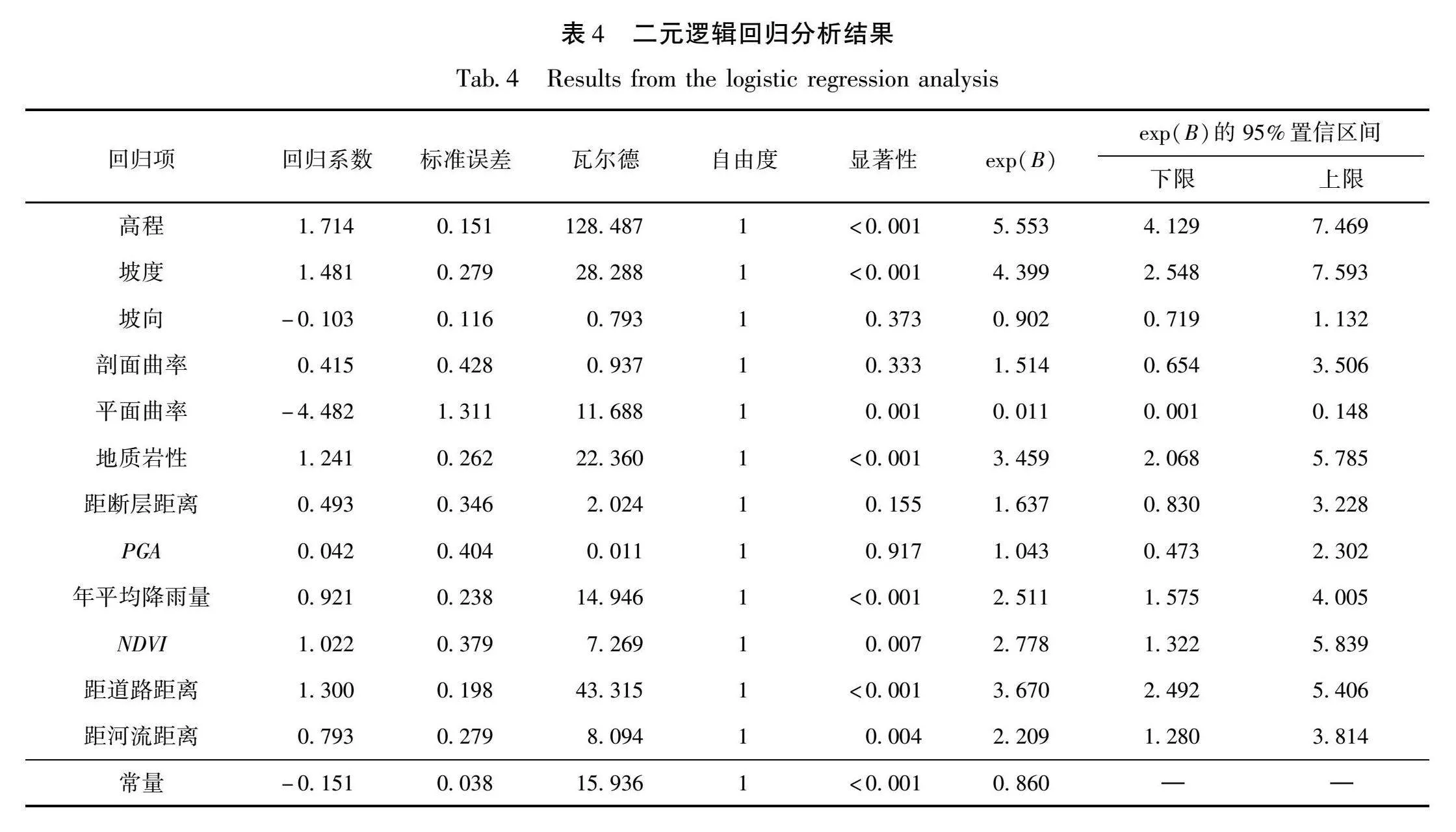
3.3 评价因子逻辑回归分析

选取训练样本集中的3 474个滑坡样本点，将各评价因子的CF值作为自变量，滑坡发生与否作为因变量，导入SPSS软件进行二元逻辑回归分析，结果见表4。由表4可知：坡向、剖面曲率、距断层距离、PGA评价因子的siggt;0.05，无数理统计意义，剔除这4个评价因子。其余评价因子siglt;0.05，评价因子权重由大到小依次为高程（1.714）、坡度（1.481）、距道路距离（1.3）、地质岩性（1.241）、NDVI（1.022）、年平均降雨量（0.921）、距河流距离（0.793）、平面曲率（-4.482）。

耦合模型下的滑坡发生概率值PCF-LR为：

PCF-LR=1/｛1+exp［-（-0.151+1.714CF1j+1.481CF2j-4.482CF3j+1.241CF4j+0.921CF5j+1.022CF6j+1.3CF7j+0.793CF8j）］｝（4）

式中：CF1j～CF8j分别表示高程、坡度、平面曲率、地质岩性、年平均降雨量、NDVI、距道路距离、距河流距离不同等级的CF值。

4 评价结果与评价精度

在ArcGIS软件中将各评价因子的CF值叠加，再根据《地质灾害风险调查评价技术要求》（FXPC/ZRZYB-01），使用自然断点法将研究区划分为极低易发区、低易发区、中易发区、高易发区以及极高易发区，分别计算得到确定性系数模型、二元逻辑回归模型及二者组成的耦合模型评价的滑坡易发性分布图，如图4所示。

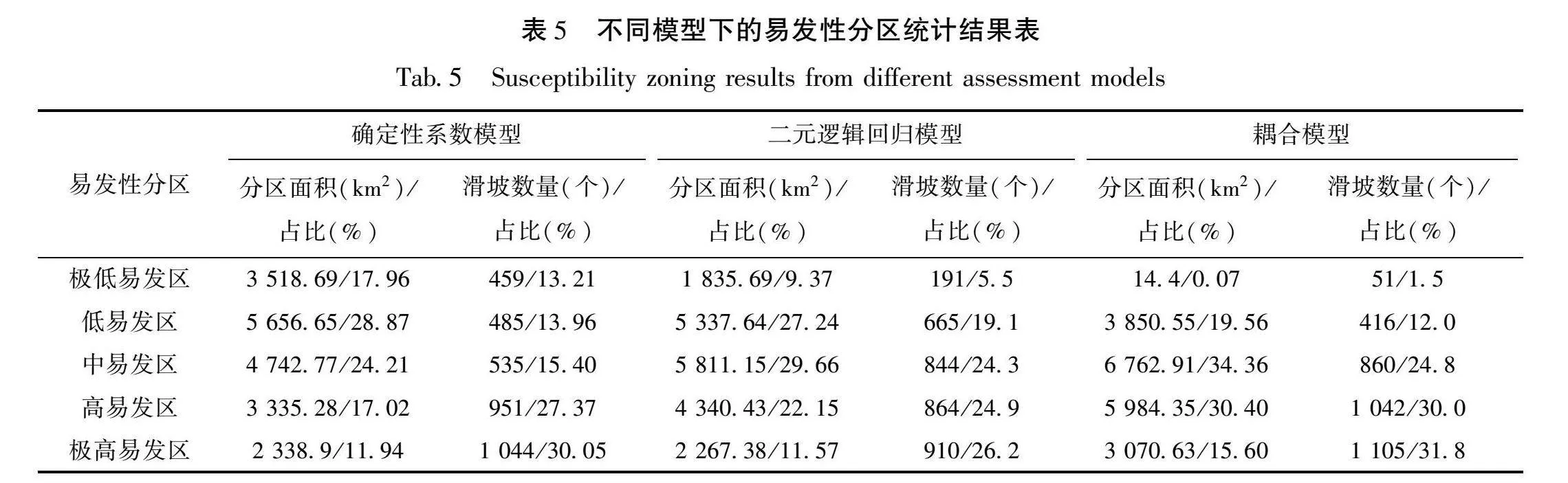
从模型评价结果（表5）中，获得的研究区滑坡易发区和滑坡分布具有以下特征：

（1）研究区滑坡极高易发区、高易发区主要发育在巧家县、鲁甸县、彝良县、大关县、永善县高海拔、坡度陡峭、地层岩性松散、距道路和河流距离相对近的区域，说明海拔、坡度、地层岩性、道路、河流等评价因子对研究区滑坡分布有显著控制作用。

（2）相比确定性系数模型与二元逻辑回归模型，耦合模型中滑坡多分布在极高易发区、高易发区，在极低易发区、低易发区分布更少。耦合模型的易发区区划与解译与野外实际灾害调查成果高度稳合，具有较好的实用性。

5 模型评价结果验证与对比分析

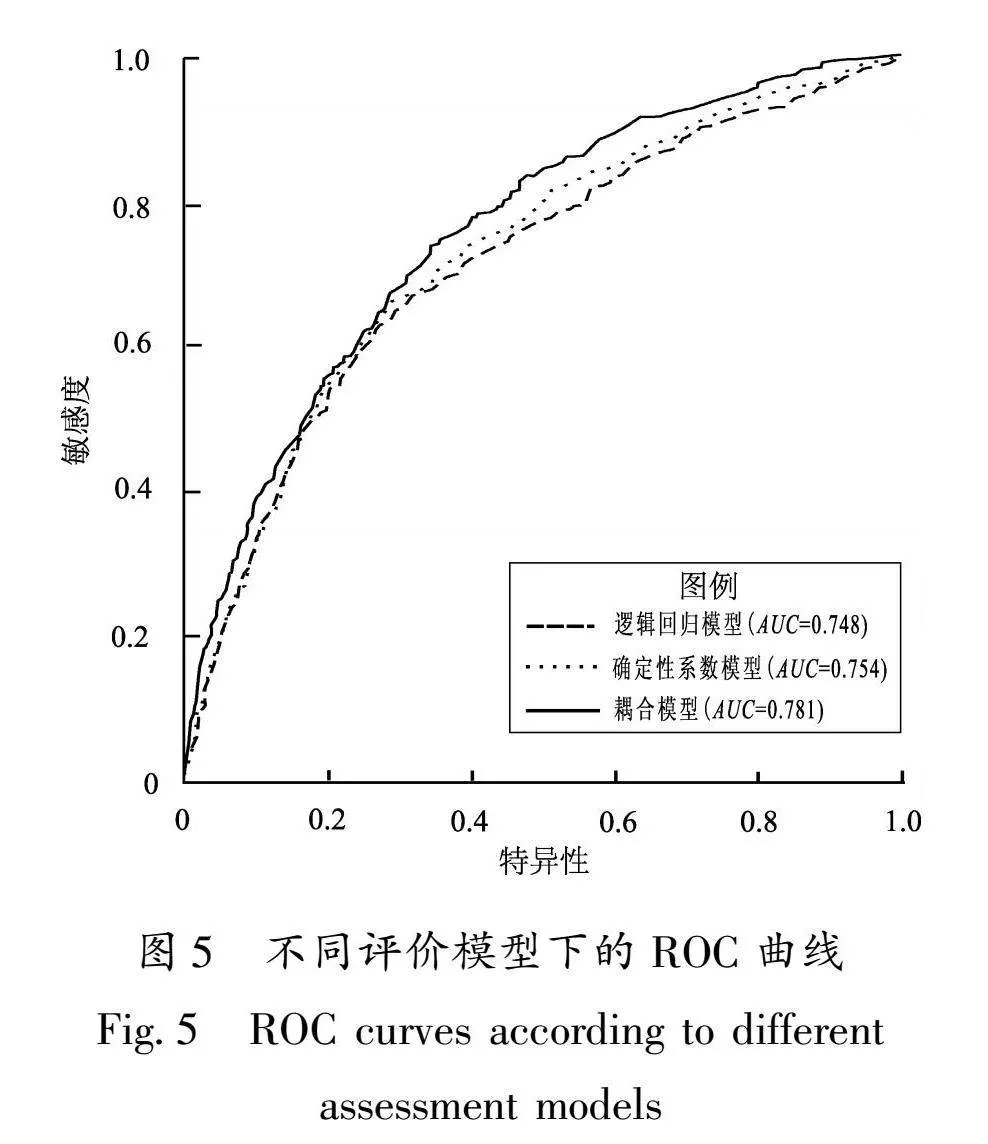
滑坡易发性评价结果与模型的可靠性紧密相关，因此需对滑坡易发性评价结果进行精度检验。将未参与训练的验证样本集中的1 488个滑坡点作为检验样本，选取ROC曲线对模型评价结果进行验证。ROC曲线检验具有试验准确性高、不受临界约束，能精准反映所用分析方法的灵敏度和特异性之间的相关性（Lee et al，2010），广泛应用于滑坡易发性评价中。AUC为ROC曲线以下至横坐标轴的面积，取值范围为0.5～1.0，值越大，表明模型评价效果越好，模型评价精度越高。确定性系数模型、逻辑回归模型及二者组成的耦合模型的ROC曲线如图5所示，AUC值分别为0.754、0.748、0.781，结果均符合模型检验要求，均准确地评价了研究区滑坡易发性，其中耦合模型的预测能力和评价精度高于单一模型。

6 讨论

本文采用3种模型对滇东北地震滑坡危险区进行了易发性评价研究，相比单一确定性系数模型或二元逻辑回归模型，耦合模型客观揭示了各评价因子对滑坡易发性影响的差异性，较好地反映了滑坡易发性评价因子之间的相互权重大小，避免了主观因素对滑坡易发性研究结果的干扰。

基于研究区滑坡点数据，采用统计学原理建立的耦合模型，优点是以实际滑坡为基础，利用滑坡影响因素对滑坡发育的贡献程度，以黑匣子方式间接地反映滑坡发育潜势（王涛等，2021），准确、客观反映了研究区滑坡发生的倾向程度。但结果仍无法反映滑坡发生的真实概率和强度。因此，需基于真实的滑坡面数据库，开展滑坡发生概率与滑坡发育规模预测研究，实现研究区滑坡危险性评价与区划。

基于耦合模型得到的滑坡易发性评价研究，揭示了研究区滑坡空间分布受高程、坡度、距道路距离、地质岩性、NDVI、年平均降雨量因素的影响程度更高。3种模型评价结果显示（图6），不同模型得到的滑坡易发性分区分布不一致，尤其是在中、低易发区分布差异较大，但在极高易发区、高易发区，滑坡整体的区划大体一致，均分布在巧家县、鲁甸县、彝良县、大关县的高海拔、坡度陡峭、地层岩性松散、距道路、河流相对近的区域，主要原因是该区域属于深切割高山峡谷地貌，地质环境脆弱，加之频繁的地震活动与强烈的构造运动，导致该地区岩体损伤弱化，岩石力学强度低，孕育了研究区脆弱的斜坡岩体赋存环境，对研究区活动断层错动、人类工程活动、降雨因数干扰的响应突出，易诱发滑坡地质灾害。

7 结论

本文以滇东北区为研究对象，选取了地形、地质、其他共3大类12个评价因子，运用GIS空间分析功能，采用确定性系数模型、二元逻辑回归模型及二者组成的耦合模型对研究区开展了滑坡易发性评价研究，取得以下结论：

（1）高程、坡度、距道路距离、地质岩性、NDVI、年平均降雨量评价因子对滑坡易发性影响相对较大，影响最大的评价因子分类级别为：高程gt;3 000 m，坡度gt;40°，距道路距离lt;100 m，地层岩性为第四系松散堆积物，NDVIlt;0.48，年平均降雨量为850～910 mm。

（2）3种滑坡易发性模型分区结果的中、低易发区分布差异较大，但极高易发区、高易发区整体的区划大体一致。中、低易发区主要分布在昭阳区、会泽县低海拔、地势平缓、人类工程活动扰动较少地区。极高易发区、高易发区主要分布在巧家县、鲁甸县、彝良县、大关县、永善县高海拔、坡度陡峭、地层岩性松散、距道路和河流距离相对近的区域。

（3）耦合模型的AUC值为0.781，高于确定性系数模型的（0.754）和二元逻辑回归模型（0.748），耦合模型评价精度、准确性高于单一模型。根据耦合模型将研究区滑坡易发区划分为极低易发区（0.07%）、低易发区（19.56%）、中易发区（34.36%）、高易发区（30.40%）、极高易发区（15.60%）。

参考文献：

郭子正，殷坤龙，刘庆丽，等.2020.基于位移比模型的三峡库区云阳县域内蠕变型滑坡降雨预警［J］.地球科学，45（2）：672-684.Guo Z Z.，Yin K，Liu Q L，et al.2020.Rainfall warning of creeping landslide in Yunyang county of Three Gorges reservoir region based on displacement ratio model［J］.Earth Science，45（2）：672-684.（in Chinese）

雷林洋.2017.基于GIS的云南省盐津县地震地质灾害危险性评价研究［D］.北京：中国地质大学（北京）.Lei L Y.2017.Study on the assessment of earthquake geohazard probability of Yanjin in Yunnan Province based on GIS［D］.Beijing：China University of Geosciences（Beijing）.（in Chinese）

林高聪，潘书华，叶振南.2021.基于Newmark法的设定地震滑坡危险性评估［J］.桂林理工大学学报，41（3）：525－532.Lin G C，Pan S H，Ye Z N，et al.2021.Assessment of landslide risk based on Newmark and preset earthquake［J］.Journal of Guilin University of Technology，41（3）：525-532.（in Chinese）

刘丽娜，许冲，徐锡伟，等.2014.GIS支持下基于AHP方法的2013年芦山地震区滑坡危险性评价［J］.灾害学，29（4）：183-191.Liu L N，Xu C，Xu X W，et al.2014.GIS-based landslide hazard evaluation using AHP method in the 2013 Lushan earthquake region［J］.Journal of Catastrophology，29（4）：183-191.（in Chinese）

罗路广，裴向军，黄润秋，等.2021.GIS支持下CF与Logistic回归模型耦合的九寨沟景区滑坡易发性评价［J］.工程地质学报，29（2）：526-535.Luo L G，Pei X J，Huang R Q，et al.2021.Landslide susceptibility assessment in Jiuzhaigou scenic area with GIS based on certainty factor and Logistic regression model［J］.Journal of Engineering Geology，29（2）：526-535.（in Chinese）

汪旭涛，谢昭宇，胡凯锋.2013.中高山地区滑坡发育地形地貌因子敏感性研究［J］.地震工程学报，35（3）：597-603.Wang X T，Xie Z Y，Hu K F.2013.Research on the sensitivity of the landform factor of landslide development in middle and high mountain areas［J］.China Earthquake Engineering Journal，35（3）：597-603.（in Chinese）

王涛，刘甲美，栗泽桐，等.2021.中国地震滑坡危险性评估及其对国土空间规划的影响研究［J］.中国地质，48（1）：21-39.Wang T，Liu J M，Li Z T，et al.2021.Seismic landslide hazard assessment of China and its impact on national territory spatial planning［J］.Geology in China，48（1）：21-39.（in Chinese）

杨德旭.2019.云南省巧家县地震前后滑坡易发性评价及地震作用影响综合研究［D］.昆明：昆明理工大学.Yang D X.2019.Comprehensive study on landslide susceptibility evaluation and seismic effect before and after earthquake in Qiaojia County，Yunnan Province［D］.Kunming：Kunming University of Science and Technology.（in Chinese）

张俊，殷坤龙，王佳佳，等.2016.三峡库区万州区滑坡灾害易发性评价研究［J］.岩石力学与工程学报，35（2）：284-296.Zhang J，Yin K L，Wang J J，et al.2016.Evaluation of landslide susceptibility for Wanzhou district of Three Gorges Reservoir［J］.Chinese Journal of Rock Mechanics and Engineering，35（2）：284-296.（in Chinese）

张晓东，刘湘南，赵志鹏，等.2018.信息量模型、确定性系数模型与逻辑回归模型组合评价地质灾害敏感性的对比研究［J］.现代地质，32（3）：602-610.Zhang X D，Liu X N，Zhao Z P，et al.2018.Comparative study of geological hazards susceptibility assessment：constraints from the information Value+Logistic Regression Model and the CF and Logistic Regression Model［J］.Geoscience，32（3）：602-610.（in Chinese）

FXPC/ZRZYB-01，地质灾害风险调查评价技术要求［S］.

FXPC/ZRZYB-01， Specification for mapping of hazard risk survey" and assessment［S］.（in Chinese）

Heckerman D.1986.Probabilistic interpretations for MYCIN s certainty factors［M］.North-Holland：Machine Intelligence and Pattern Recognition，167-196.

Lee S T，Yy T T，Peng W F，et al.2010.Incorporating the effects of topographic amplification in the analysis of earthquake-induced landslide hazards using logistic regression［J］.Natural Hazards and Earth System Sciences，10（12）：2475-2488.

Shortliffe E H，Buchanan B G.1975.A model of inexact reasoning in medicine［J］.Mathematical Biosciences，23（3/4）：351-379.

Landslide Susceptibility Assessment in Northeast Yunnan

LIU Shaochang1，BAI Xianfu1，CHU Zhengwei2

（1.Yunnan Earthquake Agency，Kunming 650224，Yunnan，China）

（2.Yunnan Southern Geological Survey Engineering Co.，Ltd.，Dali 671000，Yunnan，China）

Abstract

After studying the factors inducing landslides and the environment leading to landslides in the critical earthquake risk areas in northeast Yunnan Province，we selected 12 evaluation factors from 3 categories：“topography”，“geology”，and “others”.Then，through testing the independence of these factors，we constructed an evaluation index system of the landslide susceptibility.We randomly selected 70% of the landslide sites in the study area for the training samples of the landslide susceptibility evaluation.Using GIS spatial analysis function，we respectively used the Certainty Factor model，the Binary Logistic Regression model and the coupled model of these two models，to evaluate the landslide susceptibility in the study area.we used the rest 30% of the landslide sites for test samples，and adopted the Receiver Operating Characteristic curve to verify the accuracy of the evaluation results from the three models.We found that the evaluation factors like elevation，slope，distance from the road，geological lithology，NDVI，and average annual rainfall have relatively significant effects on the landslide susceptibility.AUC value of the coupled model is 0.781，higher than the one（0.754）of the Certainty Factor model and another one（0.748）of the Binary Logistic Regression model.The coupled model is more rational and accurate than the other two，and satisfies all the requirements of model test.The coupled model objectively revealed the difference of the influence of each evaluation factor，and well reflected the mutual weight of the influence factors of landslide susceptibility.In the study area，the predicted locations of the landslide by the coupled model is consistent with the locations determined through field survey.

Keywords：northeast Yunnan Province；landslide；susceptibility；coupling model