Bootstrap抽样下基于贝叶斯估计的地震人员死亡评估研究

摘要：选取1950—2022年中国大陆地区历史震例数据信息，以极震区烈度、发震时间及人口密度为主要影响因素，建立三级场景，运用Bootstrap抽样方法对各场景下的历史震例进行扩充，进而采用贝叶斯估计给出不同场景下地震人员死亡变化分布函数，再根据实际情况对此分布函数进行截断分析，以明确地震人员死亡的不确定性变化范围及死亡率区间概率值，最后随机选取历史地震灾害事件验证模型精度。结果表明：①各场景的死亡率均值及95%死亡率区间基本符合在极震区烈度相等并且人口密度条件下夜间死亡率大于白天死亡率的规律；②模型估计死亡人数区间能够较好覆盖实际上报的死亡人数。

关键词：地震；人员死亡；Bootstrap抽样；贝叶斯估计；死亡率

中图分类号：P315.94"" 文献标识码：A"" 文章编号：1000-0666（2025）01-0132-09

doi：10.20015/j.cnki.ISSN1000-0666.2025.0014

0 引言

地震具有突发性、波及范围广等特点，会给社会经济带来巨大损失，如建筑物倒塌、道路损毁、桥梁崩塌等基础设施的破坏，同时也可能会引发火灾、洪水等次生灾害，造成不同程度的人员伤亡。我国地处欧亚地震带和环太平洋地震带交会处，地震具有发生频次高、强度大、震源浅、分布广的特点（陈尧，2015），并且由于我国人口众多且分布相对密集，加之部分建筑结构抗震性能较差，进一步增加了地震造成人员伤亡的风险。因此，在地震发生后尽可能短的时间内，准确、快速地对地震灾情做出判断，对应急救援工作至关重要。

目前，地震人员伤亡评估方法呈现多样性，从不同的方面对地震引起的人员伤亡进行了全面的统计分析，并提出了多种可行的统计模型，如尹之潜（1991）主要从房屋破坏数量、发震时间及人口密度3个因素出发，评估不同破坏程度下的人员死亡率和受伤率；赵振东和王毅超（1998）对人员伤亡指数与状态函数之间的相互作用进行剖析，进而提出一种动态评估方法；刘金龙和林均岐（2012）分析了影响人员伤亡的主要因素，并经过函数拟合与回归分析，提出以震中烈度为主要参数，以人口密度为辅助参数进行修正的人员伤亡预测模型。赵煜等（2024a，b）根据人口密度、地理环境、建筑结构等，将中国大陆划分为西北、西南和东部三个区域，并按地震最大烈度对样本进行分类，建立粒子群优化极限学习机（PSO-ELM）地震人员死亡评估模型。在此基础上赵煜等（2024）还采用GAN对历史地震样本进行扩充，得到与原始数据集高度相似的增强数据集，以不同数据集为样本的经验模型和机器学习模型进行震后快速评估研究。在国外，Christoskov和Samardjieva（1984）给出了伤亡人数期望值和震级的关系；Badal等（2005）利用人员伤亡数量和震级之间的关联性，构造城市地区因人口密度差异引起的伤亡率变动趋势的定量模型，并验证该模型对西班牙地震活跃区域附近主要城市地震人员伤亡评估的有效性；Wald等（2011）建立了全球地震响应系统和初步评估体系，通过对震例进行测试，假设人员死亡率与地震烈度之间遵循对数正态累计分布函数关系，并用最优化方法确定模型参数，基于该模型建立了地震烈度下的人员伤亡函数模型。

在地震人员伤亡评估方法研究中，传统的经验公式法和多指标法需要输入的参数少，适用于比较粗略的震后人员伤亡快速评估，虽然在一定程度上能够评估地震影响，但仍存在局限性，无法满足救灾工作需求的精度。考虑到地震灾害数据具有稀疏性、非线性和高维度性的特点，近年来诸多学者将机器学习等智能分析方法应用于地震人员伤亡评估模型中。此类方法综合考虑了多种影响因素且不受限于传统多元线性回归方法的诸多假设，通过训练模型，学习输入数据和参数之间的复杂关系，并通过核函数等技术处理非线性关系，以达到预测目的，但这些模型更受输入数据、参数以及核函数拟合的影响，需进行调整和优化，以减小误差并提高预测准确性。

鉴于此，本文选取1950—2022年中国大陆地区5级以上历史震例数据信息，采用贝叶斯估计给出不同场景下地震人员死亡概率分布函数，从而揭示地震人员死亡的可变性范围，最后随机选取历史震例来检验模型的精确性和可信度。

1 数据来源与基础场景设定

1.1 数据来源

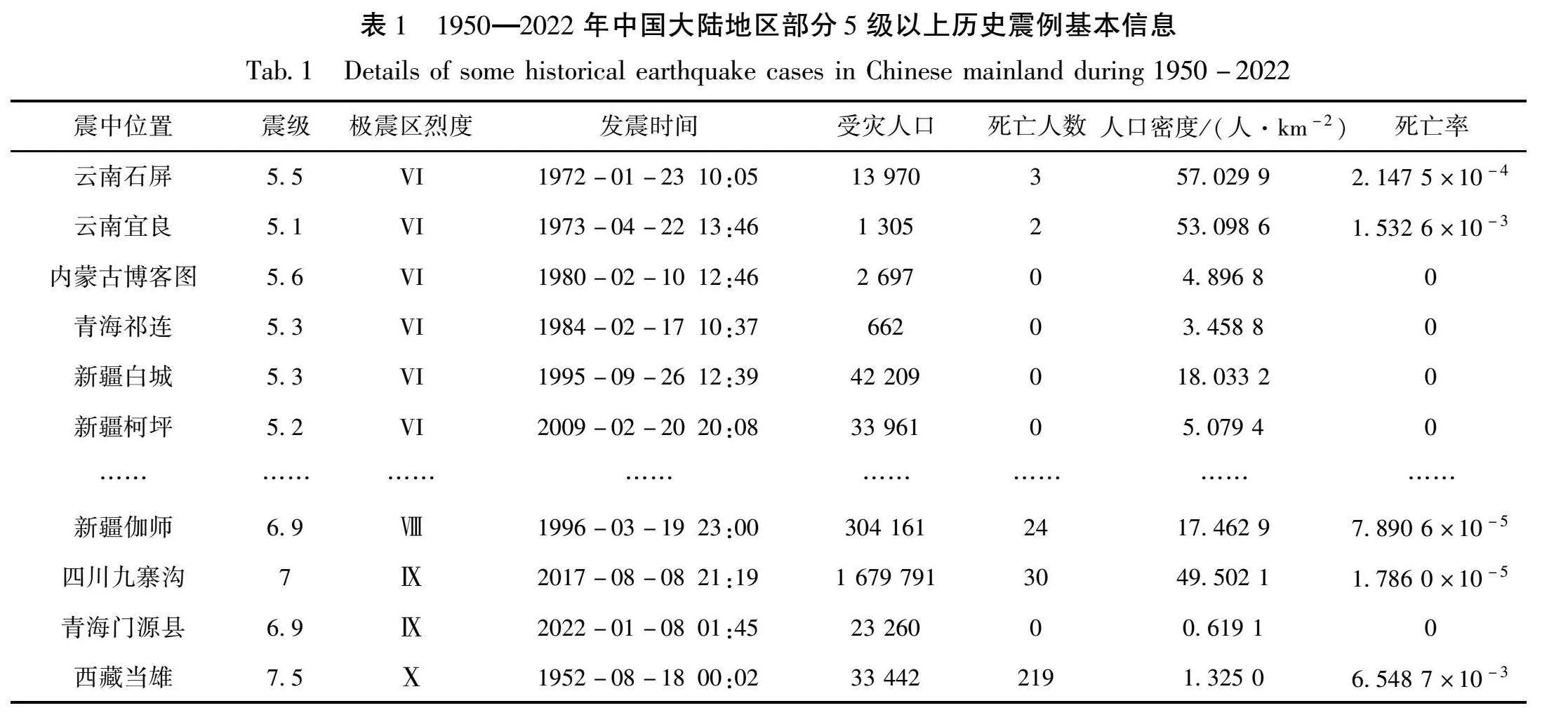
本文选取1950—2022年中国大陆地区发生的356次5级以上历史震例（表1），数据主要来源于Li等（2021）编制的1950—2018年中国大陆综合破坏性地震目录（MCCDE-CAT）、中国地震台网中心以及“中国大陆地震灾害损失评述”系列文章（郑通彦，郑毅，2012，2014，2015；郑通彦等，2015；陈通，郑通彦，2016；文鑫涛，郑通彦等，2018；文鑫清等，2021）。其中人口数据来自MCCDE-CAT和美国橡树岭国家实验室的人口栅格数据https：//landscan.ornl.gov.。

1.2 基础场景设定

本文对所选数据进行筛查，最终选取中国大陆356次历史震例的基本信息，包括极震区烈度、发震时间、人口密度、死亡人数以及受灾人口（表1）。一般极震区烈度越大，造成灾害规模及建筑破坏等级越高，相应的人员死亡率越高。发震时间对人员在室率有直接影响（周中红等，2021；谷国梁等，2021），在夜间，人员熟睡时意识和应急反应能力相对较低，无法采取紧急避险措施，更易造成人员死亡。人口密度能够反映人口分布状况，相同破坏程度的地震发生在人口密度较高的地区往往会造成更多人员死亡。极震区烈度、发震时间、人口密度这3个因素对地震人员死亡有直接的影响，因此，本文将其作为评估结果的指标。

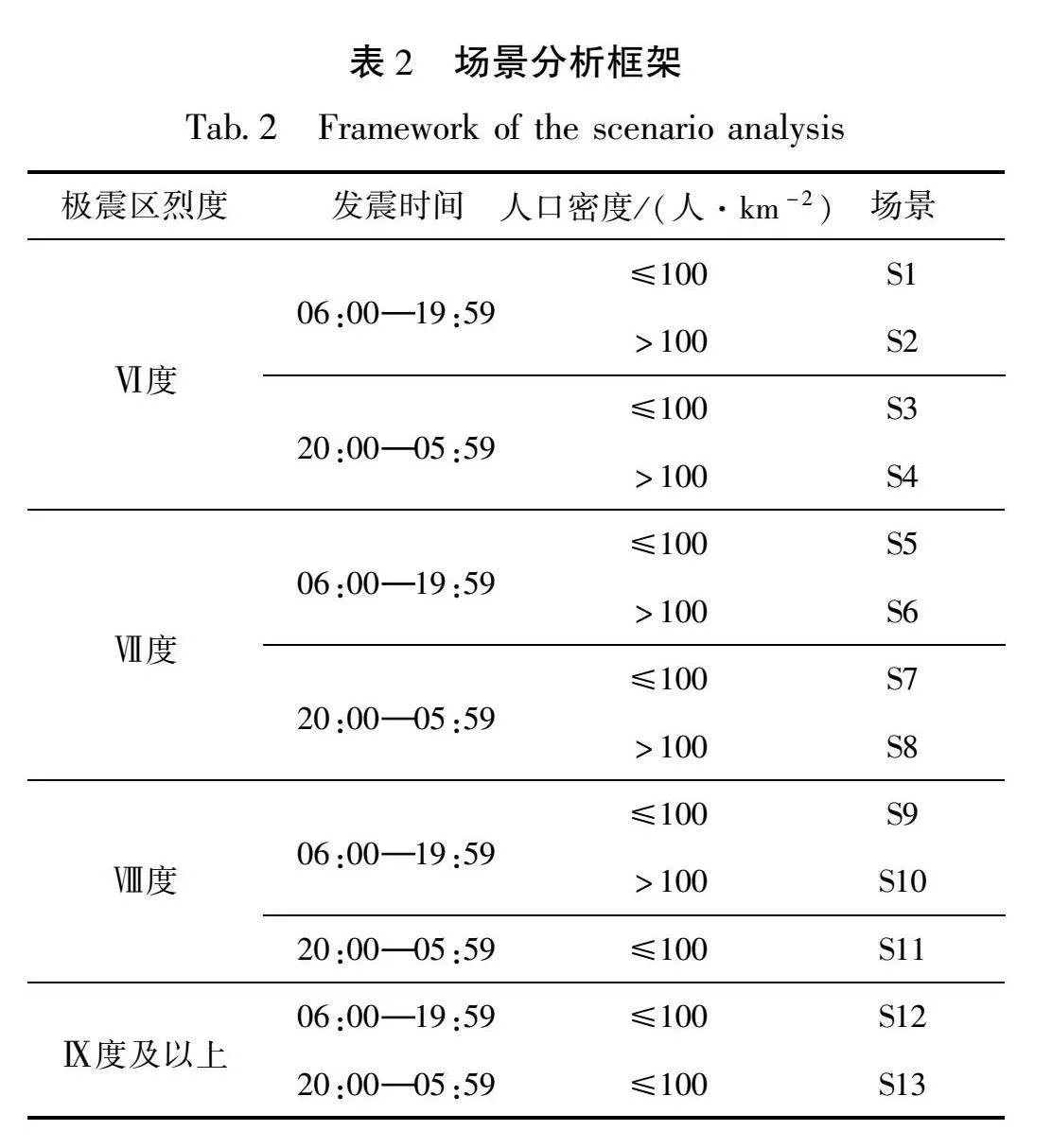
由于烈度为Ⅰ～Ⅴ度时造成人员死亡的可能性较小，根据《中国地震烈度表》（GB/T 17742—2008）中宏观调查评定地震烈度，本文只考虑极震区烈度为Ⅵ度、Ⅶ度、Ⅷ度、Ⅸ度及以上4个级别。根据中国大陆地区作息习惯将发震时间分为白天06：00—19：59和夜间20：00—05：59。最后在极震区烈度及发震时间的分级基础上，考虑人口密度对地震人员死亡的影响，将人口密度分为≤100人/km2和gt;100人/km2。由于以下3种情况案例较少，本文暂不考虑：①极震区烈度为Ⅷ度、发震时间为晚上且人口密度gt;100人/km2；②极震区烈度为Ⅸ度及以上、发震时间为白天且人口密度gt;100人/km2；③极震区烈度为Ⅸ度及以上、发震时间为晚上且人口密度gt;100人/km2。按照上述条件在考虑极震区烈度和发震时间的基础上，考虑人口密度的分级，进而构建基于极震区烈度、发震时间及人口密度的三级场景分析框架，见表2。

2 研究方法

2.1 Bootstrap抽样方法

将历史震例按照上述场景进行划分后，发现多数场景下的震例为小样本，因此采用Bootstrap抽样方法对各场景进行扩充。Bootstrap方法由Efron（1979）提出，是一种再抽样统计方法，主要用于解决小样本的评估问题，其基本思想是：在原始数据的范围内进行有效放回再抽样，样本含量仍为n，每个观察单位每次被抽到的概率相等，均为1/n，所得样本称为Bootstrap样本，如此重复X次，就可以得到X个Bootstrap样本，针对该X个样本逐一计算所关心的统计量，得到该统计量的N个观测值。通过对这些观测值进行直方图分析，可得到Bootstrap统计量的经验分布，基于该经验分布可进行统计推断及分析。

2.2 贝叶斯估计

2.2.1 地震人员死亡率参数的总体信息

本文将死亡率均值x作为随机变量，认为地震人员死亡率均值x服从正态分布即x～（μ，σ2），其概率密度函数为（茆诗松等，1998）：

f（x）=1σ2 2π e-（x-μ）22σ2（1）

式中：x为地震人员死亡率均值；μ、σ2均未知，确定这两个参数即可确定地震人员死亡率的概率密度函数。

2.2.2 地震人员死亡率参数的先验信息

将上述Bootstrap抽样结果引入先验信息，将式（1）中的2个未知参数（μ，σ2）视为随机变量，（μ，σ2）～π（μ，σ2）将其称之为先验分布（茆诗松，1999）。由于有两个参数，考虑到μ和σ2的联合概率密度函数，其表达式为：

π（μ，σ2）=π（μσ2）π（σ2）（2）

式中：π（σ2）为σ2的先验分布；π（μσ2）为条件σ2下μ的先验分布。

取逆伽马分布作为σ2的先验分布，正态分布作为μ的先验分布，即：

μσ2～N（μ0，σ2k0）σ2～IGa（v02，v0σ202）（3）

式中：μ0、k0、v0、σ20均为超参数。

2.2.3 地震人员死亡率参数的后验分布

根据贝叶斯公式及式（2），可得地震人员死亡率的后验分布公式（茆诗松等，1998）为：

π（μ，σ2x）=p（xμ，σ2）π（μσ2）π（σ2）m（x）（4）

m（x）=p（xμ，σ2）π（μσ2）π（σ2）d（μ）d（σ2）（5）

式中：p（xμ，σ2）为地震人员死亡率参数的似然函数；m（x）为样本边缘密度函数。

由于m（x）不依赖于（μ，σ2），所以式（5）可表示为：

π（μ，σ2x）∝（σ2）-［vn+12+1］exp-12σ2［vnσ2n+kn（μ-μn）2］（6）

其中：

μn=k0k0+n μ0+nk0+n x

kn=k0+n

vn=v0+n

vnσ2n=v0σ20+（n-1）s2+k0nk0+n（μ0-x）2（7）

式中：μn是先验均值μ0与样本均值x的加权平均，其权重为k0/（k0+n）和n/（k0+n），其中n为样本容量，k0为先验分布所提供的信息，于是kn=k0+n就可看作是总样本容量，后验自由度vn是先验自由度v0加上样本容量n；后验平方和vnσ2n是由先验平方vnσ20、样本平方和（n-1）s2与附加的样本均值x与先验均值μ0之差的平方和组合。

2.3 截断正态分布

本文将死亡率均值x作为随机变量构建上述地震人员伤亡的贝叶斯模型，该贝叶斯估计后验分布函数的定义域为（-∞，+∞），而根据实际情况，地震人员死亡率大于等于零，因此使用截断正态分布，对地震人员死亡率进行估计。

截断正态分布原理如下：设x～N（μ，σ2），a、b为两个已知实数，则在alt;xlt;b的条件下，x服从截断正态分布，该截断正态分布是通过将其范围外的值设置为0来修改原正态分布的概率密度函数，并将其范围内的值统一缩放，使其积分为1。

截断正态分布的概率密度函数用φ（μ，σ2，a，b，x）表示，概率密度函数（Crain，1979）表示为：

φ（μ，σ2，a，b，x）=0（x≤a）

φ（μ，σ2，x）Φ（μ，σ2，b）-Φ（μ，σ2，a）（alt;xlt;b）

0（b≤x）（8）

式中：φ（μ，σ2，x）为原正态分布的概率密度函数；Φ（μ，σ2，b）为关于右截断点的累积分布函数；Φ（μ，σ2，a）为关于左截断点的累积分布函数。

截断的正态分布的累积分布函数（Crain，1979）用Φ（μ，σ2，a，b，x）表示为：

Φ（μ，σ2，a，b，x）=0（x≤a）

Φ（μ，σ2，x）-Φ（μ，σ2，a）Φ（μ，σ2，b）-Φ（μ，σ2，a）（alt;xlt;b）

1（b≤x）（9）

截断正态分布的均值μ和方差σ2通过概率密度函数和累积分布函数确定，首先定义如下：

α=a-μσ； β=b-μσ（10）

则有：

μ=μ-σφ（0，1，β）-φ（0，1，α）Φ（0，1，β）-Φ（0，1，α）（11）

σ" 2=σ21-βφ（0，1，β）-αφ（0，1，α）Φ（0，1，β）-Φ（0，1，α）-φ（0，1，β）-φ（0，1，α）Φ（0，1，β）-Φ（0，1，α）2（12）

因为标准的概率密度函数处处都是正可积的，所以累积分布函数Φ（0，1，x）是一个在（-∞，+∞）上的严格单调函数，在开放区间（0，1）上取每一个值，只取一次，可表示为逆累积密度函数（Crain，1979）的存在，表示为Φ-1（0，1，p），返回值在（-∞，+∞）上，使得：

Φ-1［0，1；Φ（0，1；x）］（13）

Φ［0，1；Φ-1（0，1；x）］（14）

逆累积密度函数允许我们从概率0lt;plt;1开始，并返回截断值Φ-1（p）=x，使得小于或等于x的值的概率恰好是p。正态分布的逆累积密度函数有时被称为分布的“百分点”。

3 结果分析

3.1 模型结果

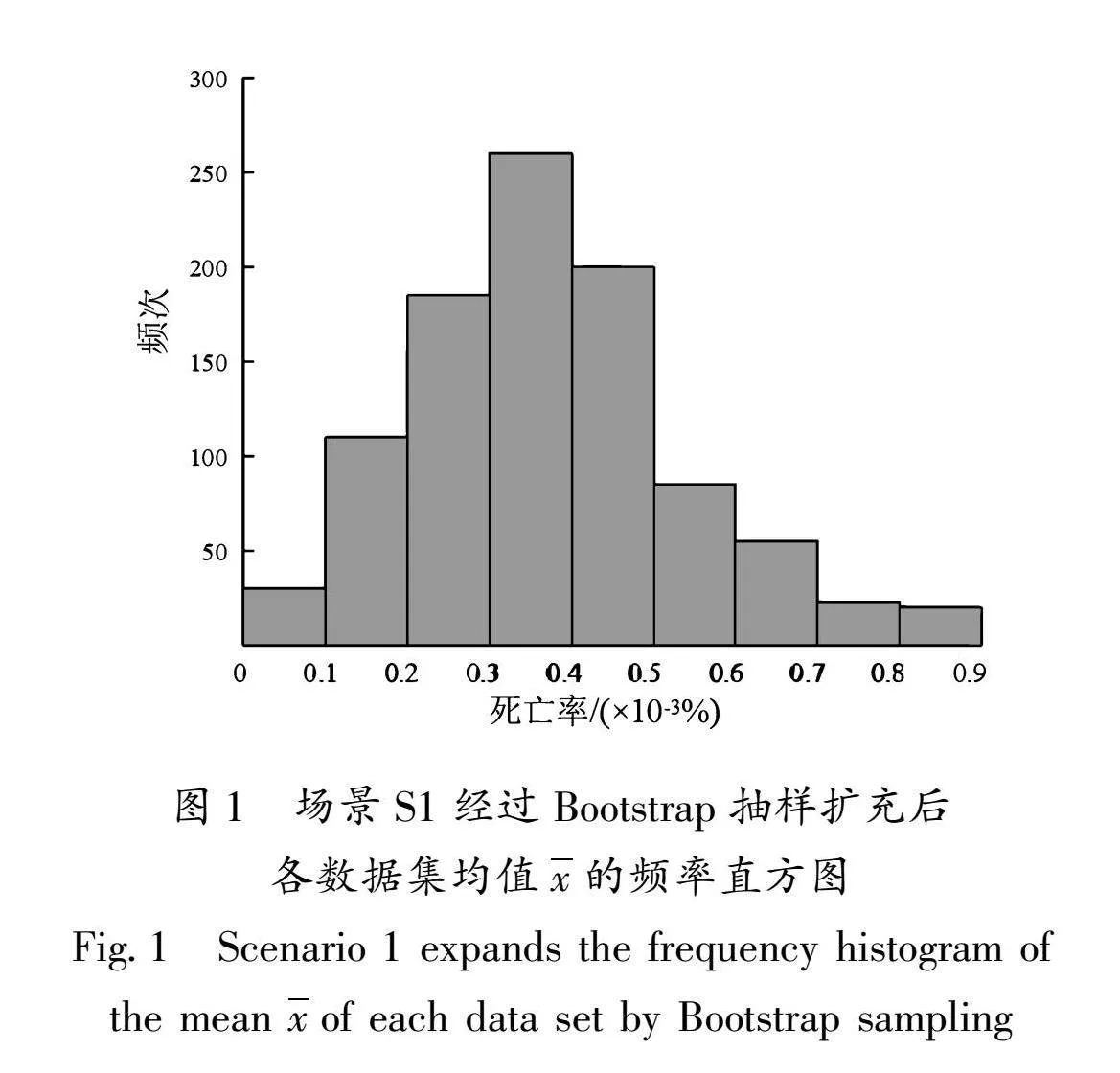
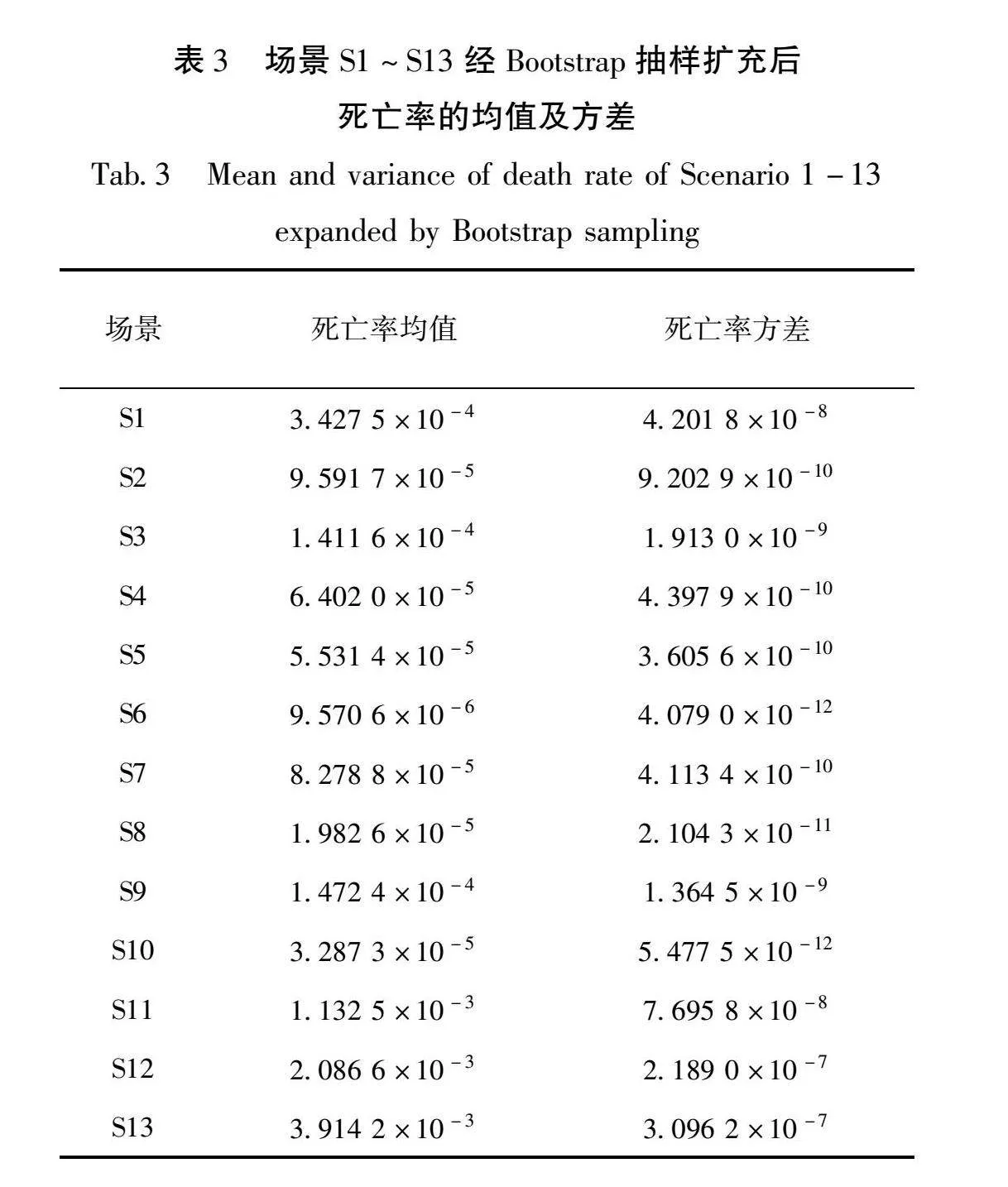
以场景S1为例，将场景S1中的死亡率通过Bootstrap抽样扩充为1 000个数据集，每个数据集中包含100个数据，再将死亡率均值x作为随机变量，拟合1 000个数据集死亡率x的频率直方图（图1），经过Bootstrap抽样扩充后各个场景死亡率x的均值、方差见表3。

为验证Bootstrap抽样扩充后死亡率数据的可用性和可靠性，将Bootstrap抽样扩充后死亡率的均值、方差（表3）与原始死亡率数据（表4）进行对比。结果表明，Bootstrap抽样扩充后的死亡率均值与原始死亡率均值特征基本一致，表明Bootstrap抽样方法能够保持样本统计量的可靠性和精确性，不会引入明显的偏差。同时死亡率方差相较于原始数据普遍偏小，该特征说明Bootstrap抽样方法有效地减少了数据的不确定性，提高了数据的稳定性和可靠性。因此Bootstrap抽样方法扩充后的虚拟数据为后续的分析和预测工作提供可靠的基础。

场景S1的死亡率均值服从x～N（3.427 5×10-4， 4.201 4×10-8），将该正态分布作为先验分布，可得超参数μ0=3.427 5×10-4，σ20=4.201 8×10-8。为了不让先验均值和方差的影响过大，取k0=v0=1。

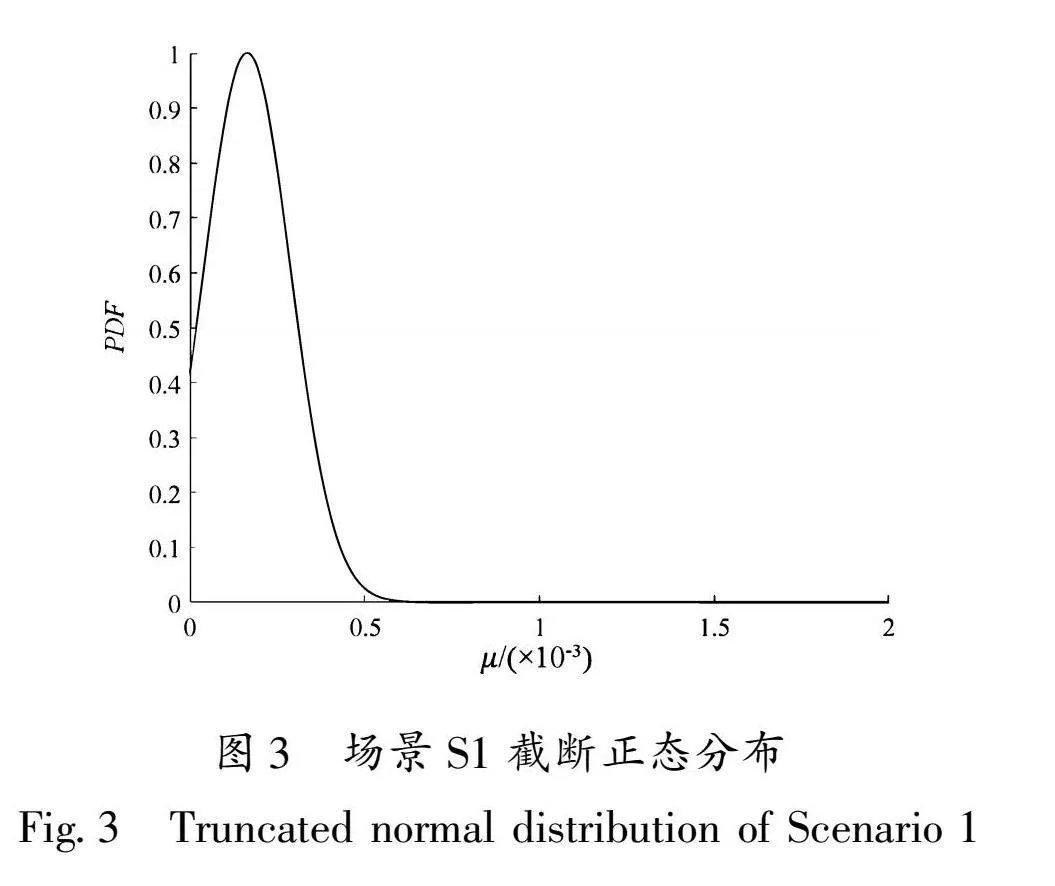
由于该数据集均值总体μ，σ2均未知，故采用正态—逆伽马分布N—IG（μn，kn，vn，σ2n）对其进行后验修正。根据联合后验密度公式可以求出后验参数值μn=3.571 7×10-7，σ2n=4.208 3×10-8，kn=vn=1 001，即后验正态—逆伽马分布为N—IG（3.571 7×10-7，1 001，1 001，4.208 3×10-8），则该正态—逆伽马分布的联合后验密度为：

π（μ，σ2 x）∝（σ2）-57exp-12σ2［1 001×4.208 3×10-8+100 1（μ-3.571 7×10-7）2］（15）

S1场景联合后分布如图2所示。由图可见，后验概率密度函数的曲面为单峰对称。根据正态近似法将其后验分布近似为正态分布，再对此正态分布进行截断分析。

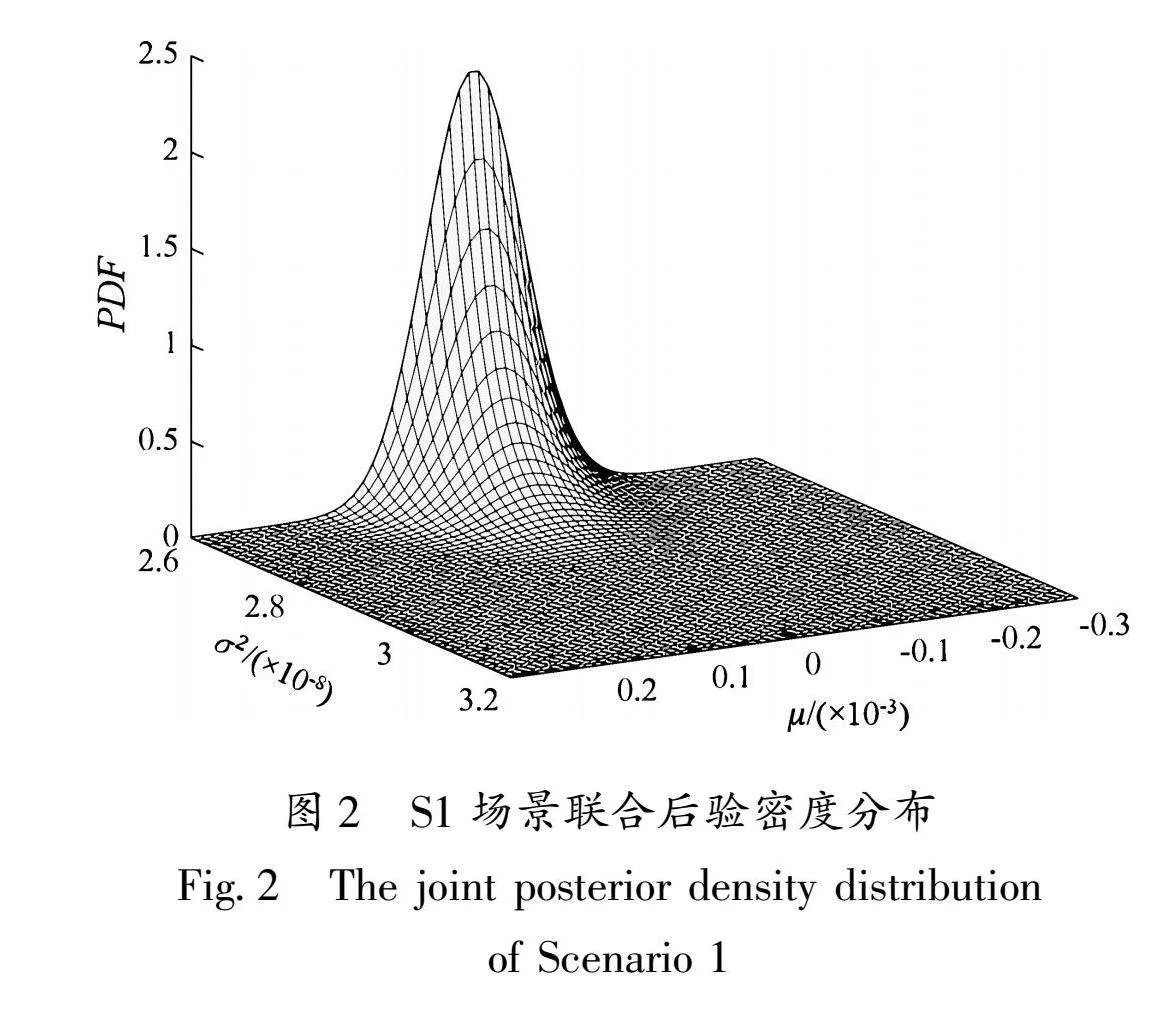
由于死亡率≥0，所以截断正态分布的范围为［0，+∞），经式（10）计算取得α=-0.001 7， β=+∞，将其带入上述x所服从的截断正态分布，可得φ（1.638 1×10-4，1.530 8×10-8，0，+∞，x），该截断正态分布如图3所示。

当该截断正态分布的逆累积分布函数为95%时，对应的死亡率为4.023 1×10-4，因此得出烈度为Ⅵ度、发震时间在白天且人口密度≤100时，95%的死亡率区间为［0，4.023 1×10-4）。

将收集的历史震例按照基础场景分级后，利用各场景下的死亡率数据结合死亡率评估模型，按照S1计算过程计算各场景下的死亡率均值以及95%的死亡率区间，见表5。由表可知，各场景下的死亡率均值及95%区间估计基本符合在极震区烈度相等并且人口密度相同的条件下，夜间的死亡率大于白天的死亡率，但在极震区烈度为Ⅵ度时，人口密度gt;100人/km2的死亡率均值及95%区间的上限值小于人口密度≤100人/km2的死亡率均值及95%区间的上限值。

3.2 模型验证

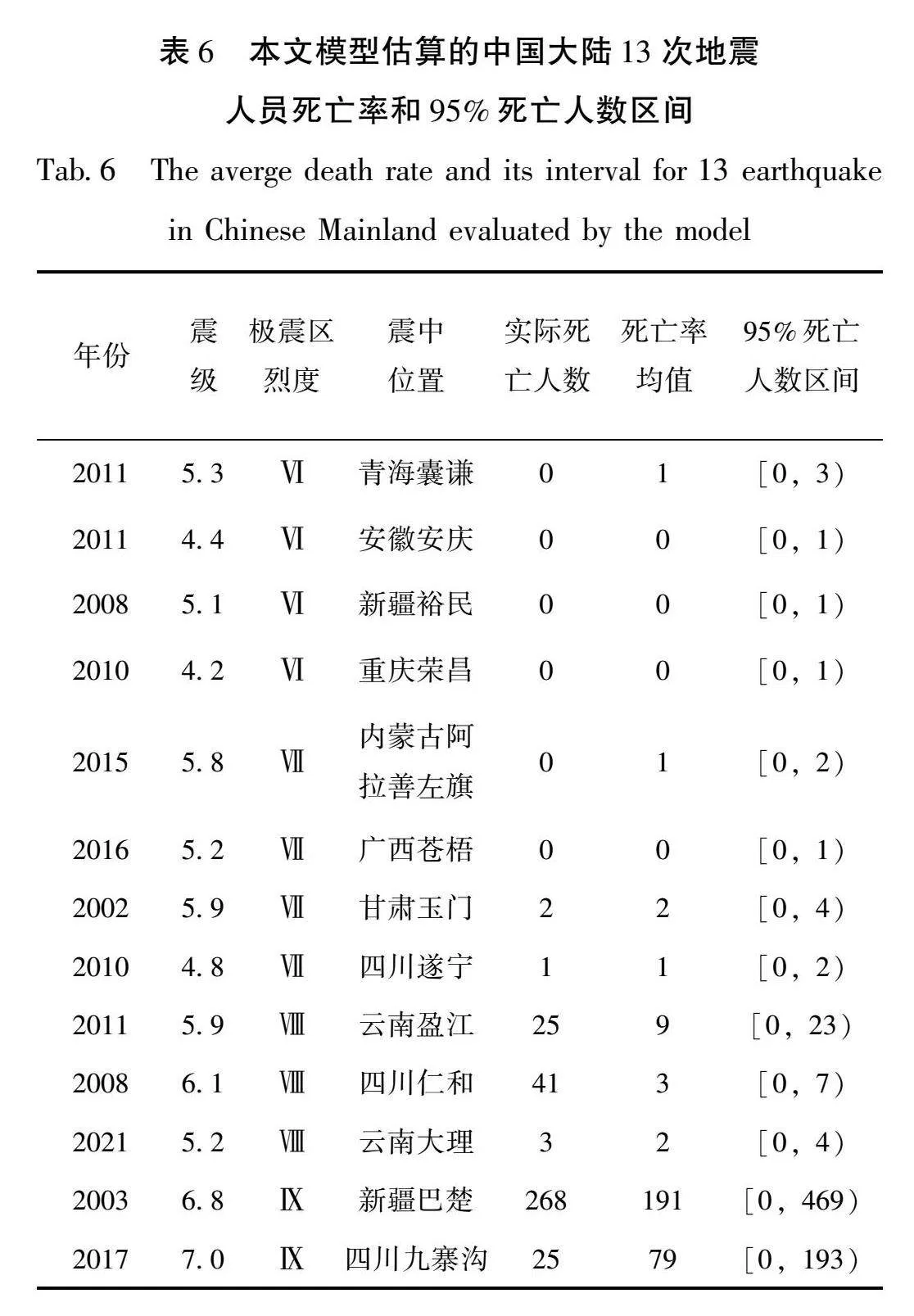
模型的准确性和可靠性，需要通过实际发生的震例进行验证，随机选取中国大陆地区13次地震的人员死亡数据，将其代入本文模型得到预测人员死亡数量，并与实际死亡人数进行对比。利用表5估算各场景下的死亡率与95%死亡人数区间，结果见表6。

由表6可见，模型总体评价效果较好，大多数震例的实际死亡人数与模型评价结果在同一数量级且被包含在区间内，评价结果较为准确。由于涉及众多不确定性因素，个别震例评估结果与实际情况存在一定出入。如模型估算的2011年云南盈江5.9级地震95%死亡人数上限值与实际死亡人数相差不大，相对来说较为合理；而2008年四川攀枝花凉山交界6.1级地震的评估结果与实际死亡人数悬殊较大，此次地震人员伤亡较多的主要原因是大量房屋倒塌和受损（张雪飞等，2008），进而导致评估结果与实际死亡人数相差较大。

4 结论

本文通过对1950—2022年中国大陆地区5级以上地震中的死亡人数进行整理和分析，选用极震区烈度、发震时间以及人口密度构建三级场景，采用Bootstrap抽样方法对各场景下的历史震例进行扩充，使用贝叶斯估计方法给出不同场景下地震人员死亡变化分布函数，最后随机选取历史地震灾害事件验证模型的精度，得出以下主要结论：

（1）从死亡率均值及95%死亡率区间结果来看，在极震区烈度为Ⅵ度时，由于场景中存在特殊震例，使地震人员95%死亡率不一定遵守夜间大于白天的一般规律。

（2）从模型验证结果来看，总体上，模型评估的95%死亡人数区间能够有效覆盖实际死亡人数，能为震后应急救援、合理地分配抗震救援和医疗人员提供决策支持和依据。

本文提出的以贝叶斯估计为主的人员死亡评估模型，给出人员死亡的概率区间，能够有效反映各场景下人员死亡的变化范围，但仍存在不足，在后续研究中有以下两点还需完善：

（1）本文研究结果受限于影响地震人员死亡因素的选取，换言之就是场景框架的建立。而实际上导致人员死亡的因素具有多样性，因此后续研究在建立地震应急基础场景时，可从完善其他影响因素数据的整理与收集入手，包括建筑物结构、次生灾害等，进而优化地震人员死亡快速评估模型，以提高模型的精度。

（2）由于我国大陆地区震例相对较少，为了获取更多震例数据，本文选取震例的时间跨度较大，应合理增加样本量。

本研究所使用的数据主要来源于南方科技大学地球与空间科学系李懿龙博士等编制的1950—2018年中国大陆综合破坏性地震目录，在此深表谢意。

参考文献：

陈通，郑通彦.2016.2015年中国大陆地震灾害损失述评［J］.灾害学，31（3）：133-137.Chen T，Zheng T Y.2016.Review of" earthquake damage losses in Chinese mainland in 2015［J］.Journal of Catastrophology，31（3）：133-137.（in Chinese）

陈尧.2015.破坏性地震人员伤亡快速评估方法研究［D］.哈尔滨：中国地震局工程力学研究所.Chen Y.2015.Study on rapid assessment method for destructive earthquake casualty［D］.Harbin：Institute of Engineering Mechanics，China Earthquake Administration.（in Chinese）

谷国梁，安立强，朱宏，等.2021.城市地震压埋人员分布评估研究——以天津市区为例［J］.地震工程学报，43（6）：1352-1360.Gu G L，An L Q，Zhu H，et al.2021.Assessment of seismic buried personnel in urban area：A case study of Tianjin urban area，China［J］. China Earthquake Engineering Journal，43（6）：1352-1360.（in Chinese）

刘金龙，林均岐.2012.基于震中烈度的地震人员伤亡评估方法研究［J］.自然灾害学报，21（5）：113-119.Liu J L，Lin J Q.2012.Study on assessment method for earthquake casualty based on epicentral intensity［J］.Journal of Natural Disasters，21（5）：113-119.（in Chinese）

茆诗松，王静龙，蹼晓龙.1998.高等数理统计［M］.北京：高等教育出版社.Mao S S，Wang J L，Pu X L.1998.Advanced mathematical statistics［M］.Beijing：Higher Education Press.（in Chinese）

茆诗松.1999.贝叶斯统计［M］.北京：中国统计出版社.Mao S S.1999.Bayesian statistics［M］.Beijing：China Statistics Press.（in Chinese）

文鑫涛，李华玥，段乙好，等.2021.2020年中国大陆地震灾害损失述评［J］.震灾防御技术，16（4）：651-656.Wen X T，Li H Y，Duan Y H，et al.2021.Earthquake disaster loss on Chinese Mainland in 2020［J］.Technology for Earthquake Disaster Prevention ，16（4）：651-656.（in Chinese）

文鑫涛，郑通彦.2018.2016年中国大陆地震灾害损失述评［J］.灾害学，33（3）：141-144.Wen X T，Zheng T Y.2018.Review of earthquake damage losses in Chinese Mainland in 2016［J］.Journal of Catastrophology，33（3）：141-144.（in Chinese）

尹之潜.1991.地震灾害损失预测研究［J］.地震工程与工程振动，11（4）：87-96.Yin Z Q.1991.A study for prediction of earthquake disaster［J］.Earthquake Engineering and Engineering Dynamics，11（4）：87-96.（in Chinese）

张雪飞，周永源，张天春，等.2008.四川攀枝花凉山交界发生6.1级地震［N］.云南日报，2008-08-31（001）.Zhang X F，Zhou Y Y，Zhang T C，et al.2008.A 6.1-magnitude earthquake struck the Liangshan and Panzhihua border region，Sichuan Province［N］.Yunnan Daily，2008-08-31（001）.（in Chinese）

赵煜，韩旭昊，孙艳萍，等.2024a.基于PSO-ELM的地震死亡人员评估方法研究［J］.地震工程学报，46（3）：742-750.Zhao Y，Han X H，SUN Y P，et al.2024a.Research on earthquake fatality assessment method based on PSO-ELM［J］.China Earthquake Engineering Journal，46（3）：742-750.（in Chinese）

赵煜，李娅妮，孙艳萍，等.2024b.基于GAN的地震人员死亡样本扩充方法研究［J］.灾害学，39（4）：40-46.Zhao Y，Li Y N，SUN Y P，et al.2024b.Research on earthquake fatalities sample augmentation method based on GAN［J］. Journal of Catastrophology，39（4）：40-46.（in Chinese）

赵振东，王毅超.1998.地震人员伤亡指数与人员伤亡状态函数［J］.自然灾害学报，7（3）：90-96.Zhao Z D，Wang Y C.1998.The index and state-function of casualties in earthquake［J］.Journal of Natural Disasters，7（3）：90-96.（in Chinese）

郑通彦，冯蔚，郑毅.2015.2014年中国大陆地震灾害损失述评［J］.世界地震工程，31（2）：202-208.Zheng T Y，Feng W，Zheng Y.2015.Review of" earthquake damage losses in Chinese Mainland in 2014［J］.World Earthquake Engineering，31（2）：202-208.（in Chinese）

郑通彦，郑毅.2012.2011年中国大陆地震灾害损失述评［J］.自然灾害学报，21（5）：88-97.Zheng T Y，Zheng Y.2012.Review of earthquake damage losses in Chinese Mainland in 2011［J］.Journal of Natural Disasters，21（5）：88-97.（in Chinese）

郑通彦，郑毅.2014.2012年中国大陆震灾害损失述评［J］.自然灾害学报，23（3）：166-170.Zheng T Y，Zheng Y.2014.Review of earthquake disasters in Chinese mainland" in 2012［J］.Journal of Natural Disasters，23（3）：166-170.（in Chinese）

郑通彦，郑毅.2015.2013年中国大陆地震灾害损失述评［J］.自然灾害学报，24（1）：239-246.Zheng T Y，Zheng Y.2015.Review of earthquake damage losses in Chinese Mainland" in 2013［J］.Journal of Natural Disasters，24（1）：239-246.（in Chinese）

周中红，陈文凯，何少林，等.2021.甘肃省不同地区不同时段人员在室率研究［J］.震灾防御技术，16（3）：501-509.Zhou Z H，Chen W K，He S L，et al.2021.Study on in-building probability of different periods and different regions in Gansu Province［J］.Earthquake Disaster Prevention Technology，16（3）：501-509.（in Chinese）

GB/T 17742—2008，中国地震烈度表［S］.GB/T 17742—2008，China seismic intensity scale［S］.（in Chinese）

Badal J，Vázquez-prada M，lvaro González.2005.Preliminary quantitative assessment of earthquake casualties and damages［J］.Natural Hazards，34（3）：353-374.

Christoskov L，Samardjieva E.1984.An approach for estimation of the possible nuámber of casualties during strong earthquakes［J］.Bulgarian Geophysical Journal，10（4）：94-106.

Crain B R.1979.Estimating the parameters of a truncated normal distribution［J］.Applied Mathematics amp; Computation，5（2）：149-156.

Efron B.1979.Bootstrap methods：another look at the jackknife［J］.The Annals of Statistics，7（1）：1-26.

Li Y L，Zhang Z G，Xin D H.2021.A composite catalog of damaging earthquakes for Chinese mainland［J］.Seismol Res Lett，92（6）：3767-3777.

Wald D J，Jaiswal K S，Marano K D，et al.2011.Earthquake impact scale［J］.Natural Hazards Review，12（3）：125-139.

Estimation of Earthquake Deaths Based on the Bayesian Estimationby the Bootstrap Sampling

ZHAO Yu1，WEI Maomao1，SUN Yanping2，SHI Yitong2，CHEN Wenkai2

（1.College of Statistics and Data Science，Lanzhou University of Finance and Economics，Lanzhou 730020，Gansu，China）

（2.Lanzhou Institute of Seismology，China Earthquake Administration，Lanzhou 730020，Gansu，China）

Abstract

The rapid post-earthquake assessment of the earthquake-caused casualty is crucial for decision-making and deployment of emergency response in earthquake scenarios.In this study，historical seismic data in Chinese mainland from 1950 to 2022 were selected for assessing the impact factors including the seismic intensity in the meizoseismal area，the original time，and the population density.Three levels of scenarios were established，and the Bootstrap sampling method was applied to expanding the historical seismic data for each scenario.Tthe Bayesian estimation was then employed in obtaining the distribution functions of the earthquake-caused casualties for different scenarios.Furthermore，truncation analysis was conducted based on real situations to determine the uncertainty range and the probability of mortality rate intervals.Finally，historical earthquake disasters were randomly selected to validate the accuracy of the model.The results showed that：①The mean and 95% interval estimates of the death rate of each scene basically accord with that the death rate of night in higher than that of day under the condition of the same intensity and the same population density in the earthquake area. ②The range of expected casualties estimated by the model effectively covered the actual statistical deaths.

Keywords：earthquake；earthquake-caused death；the Bootstrap sampling；the Bayesian estimation；death rate