被动柔性防护系统中减压环力学性能研究

摘要

减压环是被动柔性防护系统中重要的耗能装置，深入研究减压环力-位移关系对减压环设计和被动柔性防护系统性能具有重要意义。基于“等能量”原则，提出一种减压环力-位移关系双折线简化模型的方法。考虑材料非线性和几何非线性的影响，采用LS-DYNA软件建立减压环有限元模型，模拟了减压环在匀速动荷载作用下的拉伸过程，研究了钢管壁厚、钢管管径、钢管环径、铝套筒长度、铝套筒厚度和预紧力大小等因素对双折线模型参数第一刚度、第二刚度及屈服强度的影响，并给出了3个参数的拟合公式。研究表明，改变钢管壁厚、管径或环径会有效改变减压环的力学性能和耗能能力，改变铝套筒的长度或厚度对减压环的力-位移曲线影响较小，但过小的铝套筒厚度容易导致套筒发生撕裂破坏。

关键词

减压环;数值模拟;力-位移曲线;简化拟合参数;耗能

中图分类号：O242.21；U213.8"" 文献标志码：A"" 文章编号：1004-0366（2024）06-0050-08

被动柔性防护系统是一种常见的边坡落石灾害防治结构，一般由金属拦截网片、钢柱、耗能装置、钢丝绳等构件组成［1］。耗能器是被动柔性防护系统的重要耗能和缓冲装置［2］，承担整个系统60%以上的耗能［3］。减压环是一种结构简单，耗能能力强的耗能器，在被动柔性防护系统中得到广泛应用。目前国内工作能级500 kJ以上的被动柔性防护系统普遍采用GS-8002型减压环，每个减压环可消耗大约60 kJ的冲击能［4］。减压环由钢管、铝套筒、钢丝绳3部分组成，如图1所示。

目前减压环力-位移关系和耗能机制的研究方法主要包括拟静力试验和数值模拟。CASTRO-FRESNO等［5］对单套筒减压环与双套筒减压环进行了拟静力拉伸试验和数值模拟，研究了摩擦因数、预紧力对减压环耗能性能的影响。GENTILINI等［6］通过减压环拟静力拉伸试验获取了减压环力-位移关系曲线，对力-位移关系曲线进行简化并应用于被动柔性防护系统的数值模拟。汪敏等［7］通过对GS-8000型减压环拟静力试验和数值模拟，研究了不同拉伸速度对减压环的力-位移曲线的影响，发现随着冲击荷载速度的增加，减压环的启动荷载和耗能能力也逐渐增大。刘成清等［8］对GS-8000型减压环进行了拟静力试验和有限元仿真，拟合得到了减

压环三折线荷载-位移曲线，并对比了落石冲击情况下，安装与不安装减压环对被动柔性防护系统动力响应的影响，证明减压环可有效提高被动柔性防护系统的柔性。赵雅娜等［9］提出了一种适用于多跨式被动柔性防护系统的数值计算方法，在模拟减压环力-位移关系时提出了用启动荷载T0、最大拉伸荷载Tr、最大伸长量Lr 3个性能参数来描述减压环的拉伸工作过程，并根据这3个参数给出了串并联减压环刚度公式。齐欣等［10］对串、并联减压环组进行了动力冲击试验，得到了动力荷载作用下减压环的荷载-时间曲线，并分析了动力荷载作用下减压环组的变形和受力特征，给出了4折线的等代曲线模型。黄俊飞［11］对GS-8002减压环进行了中性盐雾腐蚀试验，并通过拟静力拉伸试验对比研究了不同腐蚀程度对减压环力-位移关系的影响，得到了减压环启动力、耗能能力与腐蚀后失重率的相关关系。

综上可知，目前国内外对减压环的研究主要思想是将减压环复杂的力-位移关系简化成双折线或多折线，以便于对被动柔性防护系统整体性能进行研究。但既有文献大多以钢丝绳荷载大小作为折线参数，而减压环在动力拉伸过程中荷载高低起伏变化较大，以荷载大小确定参数容易引起较大误差。本文尝试从“等能量”角度出发，兼顾减压环受力特点，以减压环自身刚度属性为基础，提出减压环力-位移关系的简化方法，然后通过数值方法系统研究铝套筒几何尺寸、铝套筒预紧力、钢管几何尺寸等因素对简化力-位移曲线各参数的影响，并给出力-位移曲线各参数的拟合公式，为被动柔性防护系统研究和减压环设计提供依据。

1 减压环数值模拟

减压环在冲击荷载作用下的响应较为复杂，涉及材料非线性、几何非线性、摩擦接触等问题［12］。采用LS-DYNA软件建立减压环数值模型，进行等速率冲击荷载作用下的减压环拉伸过程的数值模拟。建模以GS-8002减压环的尺寸为基础，钢管环径为460 mm，钢管管径为42 mm，钢管壁厚为3 mm，铝套筒长度为70 mm，铝套筒壁厚为13.5 mm。

1.1 单元类型

钢管与铝套筒采用solid164单元。考虑到钢丝绳抗弯刚度较低，主要承受轴向荷载［13］，故采用link160单元模拟。减压环网格单元如图2所示。

1.2 材料本构

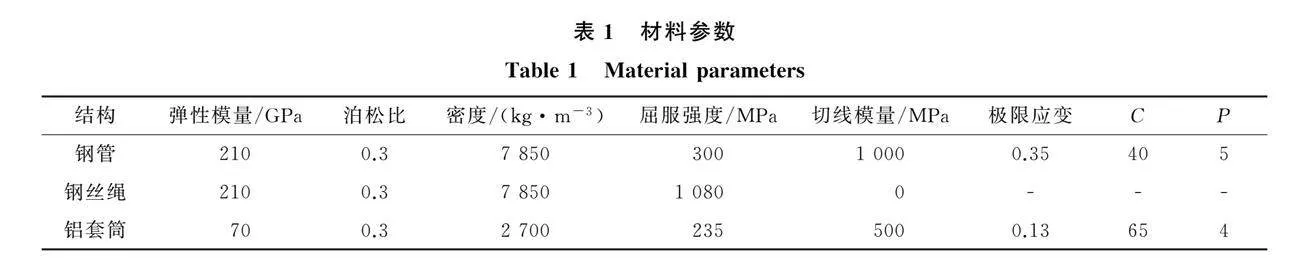
减压环各部件的材料参数如表1所列［8］。钢管、铝套筒采用塑性随动强化模型;钢丝绳采用双线性随动模型。钢材的切线模量采用真实应力-应变曲线［14］中的强化阶段的斜率。

由于钢管与铝套筒之间接触速率较大，应考虑材料应变率的影响［15］，故采取cowper-symonds模型模拟材料的应变率产生的硬化效应。应变率与屈服应力的关系为

σy=1+εC1P（σ0+βEpεeffp）， （1）

其中：σy为考虑应变率影响下的屈服应力;σ0为初始屈服应力;ε和εeffp分别为应变率和有效塑性应变;β为硬化参数;Ep为塑性硬化模量;C、P均为应变率参数，取值见表1。

1.3 接触

在减压环的实际工作过程中存在3个接触：钢管与铝套筒之间的接触;钢管与钢管自身的接触;钢管与钢丝绳之间的接触。在数值模拟中，钢管与钢丝绳之间采用自动梁面接触;考虑到钢管和铝套筒接触面需要进行双向检查防止穿透，采用自动面面接触;同理，钢管与钢管之间亦采用自动面面接触。接触类型与参数如表2所列。

接触过程中的摩擦系数由动摩擦因数、静摩擦因数、接触面相对速度共同决定，摩擦系数的表达式为

μc=FD+（FS-FD）e-DC|vrel|， （2）

其中：FS为静摩擦因数;FD为动摩擦因数;DC为指数衰减系数［16］;vrel为接触面相对速度。

1.4 边界条件

数值模拟过程中对减压环钢丝绳一端进行铰接固定，另一端使用速度荷载匀速进行拉伸。

1.5 加载方式

根据减压环在被动防护系统中的实际工作状况［17］，钢丝绳匀速拉伸速度为20 m/s。减压环最大拉伸位移取减压环的周长的70%，即取最大拉伸位移为1 m。

2 减压环力-位移曲线简化

2.1 仿真结果验证

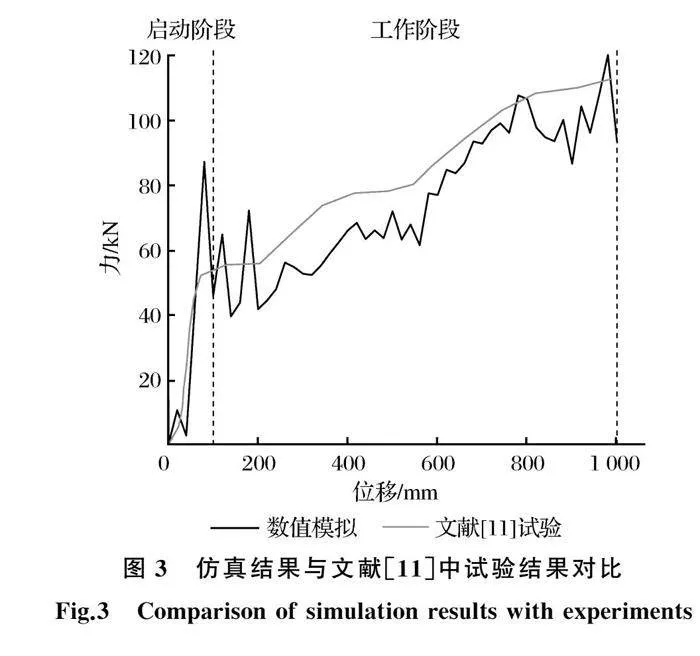
对GS-8002减压环基础模型进行仿真求解得到减压环的力-位移曲线，将仿真结果与文献［11］中拟静力试验结果进行对比（见图3），发现仿真结果与试验结果较为吻合，验证了模型的正确性。

2.2 阶段特征

根据文献［11］中试验与仿真模拟中减压环的力-位移曲线可知，减压环的受力过程可分为启动阶段与工作阶段。启动阶段减压环的力-位移曲线基本呈线性关系，此阶段内钢管和铝套筒未发生相对滑动，系统刚度为铝套筒和钢管组成的结构刚度。当拉伸位移达到最大拉伸位移的10%左右时［4］，钢管和铝套筒发生相对滑动，铝套筒不再对系统提供刚度，系统刚度仅由钢管提供，力-位移曲线经历短暂震荡后缓慢上升，耗能机制由钢管和铝套筒的摩擦耗能、钢管本身的屈服变形耗能组成。

2.3 简化原则与简化方法

根据减压环力-位移关系曲线特点，简化原则如下：（1）遵循“等能量”原则，即简化后曲线与x轴围成的面积和数值模拟曲线与x轴围成的面积相等;（2）遵循主要力学参数等效原则，即简化后曲线的主要力学参数及工作阶段要与数值模拟曲线相符。

由以上分析可知，减压环的力-位移关系分为启动阶段与工作阶段，故将减压环的力-位移关系简化为双折线模型，其主要力学参数为K1、 K2、T0，如图4所示。图4中K1为减压环第一刚度，即启动阶段的力-位移曲线的斜率;K2为减压环第二刚度，即工作阶段力-位移曲线的斜率;T0为减压环的屈服强度，x1为启动阶段的最大位移;x2为减压环最大拉伸位移，一般取x1=0.1x2。

K1、K2、T0的确定方法如下：采用最小二乘法对工作阶段力-位移曲线进行拟合，K2取拟合直线的斜率。根据“等能量”原则，令工作阶段简化前后的耗能Q相等（Q通过数值模拟结果得到），即可得到

（T0+T0+K2Δx）Δx2=Q， （3）

其中：Δx=x2-x1。经整理，有

T0=QΔx-K2Δx2。 （4）

然后可由屈服强度T0确定第一刚度K1：

K1=T0x1。 （5）

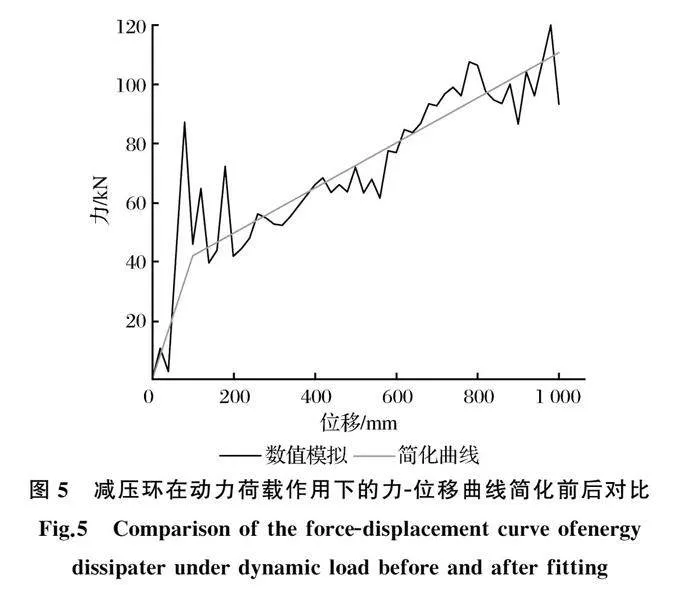
GS-8002减压环在匀速动荷载作用下的力-位移曲线简化前后的对比见图5。该简化方法确保了减压环在工作阶段耗能大小的一致性，并兼顾了减压环受力特性。简化曲线应用于被动柔性防护系统模型，既节省了计算工作量，又能保证耗能和受力等效。

3 减压环参数对力-位移曲线的影响与分析

3.1 钢管壁厚

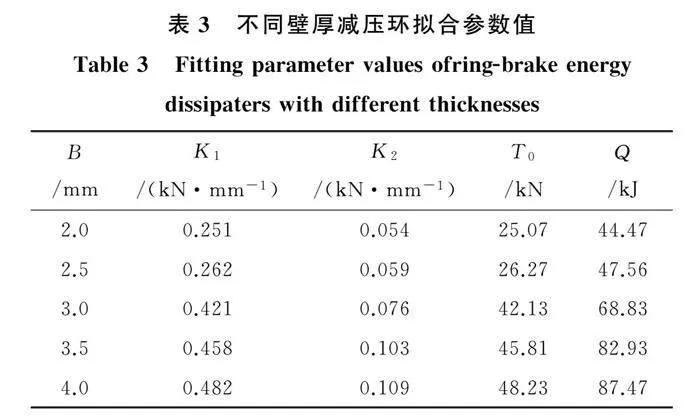
建立钢管厚度B分别为2 mm、2.5 mm、3 mm、3.5 mm、4 mm的5个减压环模型。不同钢管壁厚减压环力-位移曲线见图6，简化曲线拟合参数见表3。

由图6和表3可见，随着壁厚的增加，K1、K2、T0和Q均有不同程度的增大趋势。这是因为增加壁厚会增加钢管截面的抗弯刚度和强度，而钢管抗弯刚度对K1、K2有贡献，钢管抗弯强度对T0有贡献，且增加壁厚也对钢管在工作阶段的屈服变形耗能机制有贡献。因此，适当增加减压环壁厚可改善其力学性能，增加耗能能力。

3.2 钢管管径

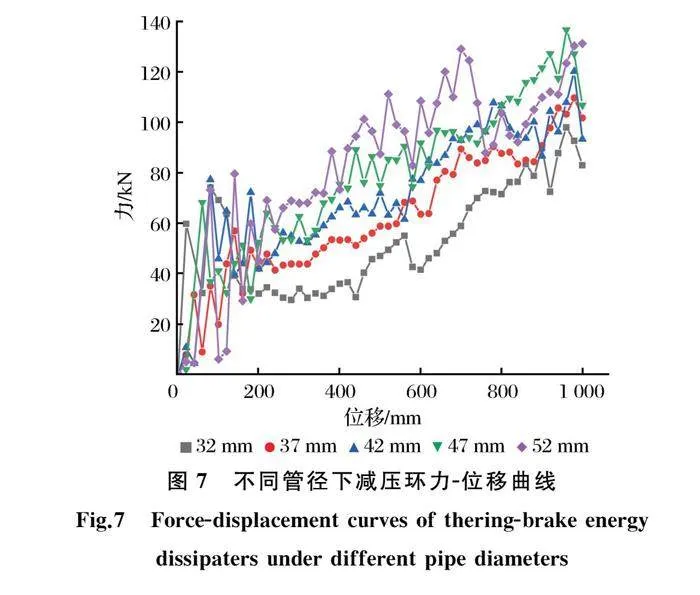
建立管径T分别为32 mm、37 mm、42 mm、47 mm、52 mm的5个减压环模型。不同钢管管径的减压环力-位移曲线见图7，简化曲线拟合参数见表4。

由图7和表4可见，随着管径的增加，K1、T0和Q均有不同程度的增大。原因是增加管径会增加钢管截面抗弯刚度、强度，以及增加钢管和铝套筒的摩擦接触面积。K2也是随着壁厚增加呈递增趋势，但在52 mm时突然递减，原因是管径增加而壁厚不变的情况下，钢管越来越趋近于薄壁空心结构，很容易引起管壁局部屈区。因此适当增加管径会改善减压环的力学性能和耗能能力，但应避免管径太大导致的局部屈区现象。

3.3 减压环环径

建立钢管环径D分别为400 mm、430 mm、460 mm、490 mm、520 mm的5个模型。不同钢管环径的减压环力-位移曲线见图8，简化曲线拟合参数见表5。

由图8和表5可见，随着减压环环径的增加，K1、K2呈递减趋势，原因是增加管径降低了钢管的抗弯刚度。随着环径的增加，T0出现小幅震荡递增后递减的趋势，理论上随着环径的增加，T0应呈现下降趋势，但由于管径增加也导致减压环最大拉伸长度增加，不同的最大拉伸长度在一定程度上影响了T0的数值。减压环耗能能力出现先递增后递减的趋势，这是K2递减和最大拉伸长度递增双重因素影响的结果。

3.4 预紧力

在减压环拉伸之前，减压环在实际加工情况下一般会对铝套筒表面施加一定的预紧力［18］。施加预紧力可以使钢管与铝套筒接触得更加紧密。分别施加20 MPa、35 MPa、50 MPa、65 MPa、80 MPa的预紧力F，然后进行减压环拉伸数值模拟。不同预紧力作用下减压环力-位移曲线见图9，简化曲线拟合参数见表6。

由图9和表6可见，随着预紧力的增加，T0呈递增的趋势，当预紧力增加至50 MPa后，T0增长极其缓慢;K1基本呈递增趋势;K2无明显变化规律;随着预紧力的持续增加，结构的耗能从64.9 kJ增加至69.5 kJ，但耗能变化不大。预紧力的增加会加大钢管与铝套筒之间的最大静摩擦力，进而会增加减压环的屈服强度。增加预紧力不改变钢管的刚度，所以预紧力的增加对减压环的K2无明显影响，仅使得减压环的K1有较小的增加趋势。

3.5 铝套筒长度

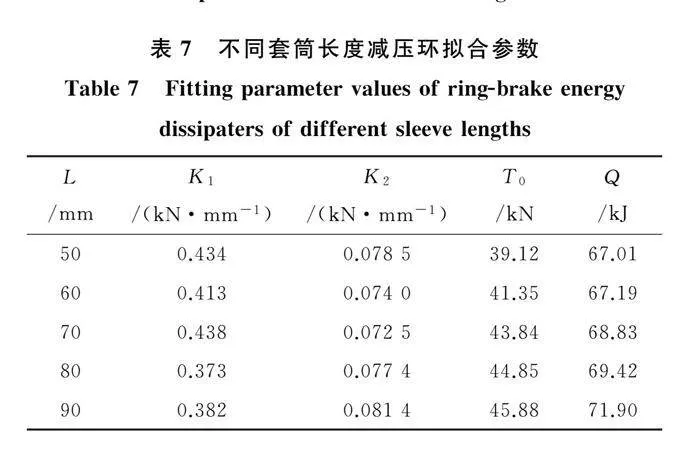
建立铝套筒长度L分别为50 mm、60 mm、70 mm、80 mm、90 mm的5个减压环模型。不同铝套筒长度的减压环力-位移曲线见图10，简化曲线拟合参数见表7。

由图10和表7可见，随着铝套筒长度的增加，T0呈递增趋势，K1、K2无明显变化规律。说明铝套筒长度的增加会加大套筒与钢管之间的摩擦力，使得屈服强度T0增加，但不改变钢管的刚度，使得K1、K2无明显变化规律。

3.6 铝套筒厚度

建立铝套筒厚度TB分别为8.5 mm、11 mm、13.5 mm、16 mm的4个减压环模型。不同铝套筒厚度的减压环力-位移曲线见图11，简化曲线拟合参数见表8。

由图11和表8可见，随着铝套筒厚度的增加，K1呈缓慢递增趋势，K2、T0和Q均表现为先递增后递减的趋势，但数值变化不大，在厚度为13.5 mm时出现极值。当铝套筒厚度为8.5 mm时，减压环的力-位移曲线在500 mm后出现急剧下降的趋势，这是由于铝套筒厚度不够发生强度破坏（见图12）。减压环厚度变化对各参数的影响不大，但应注意厚度值不能太小，以免拉伸过程中发生强度破坏。

4 减压环力-位移曲线参数公式拟合

根据不同影响因素作用下减压环拟合参数K1、K2、T0产生的变化规律进行总结，发现对K1产生影响的因素有钢管壁厚、钢管管径、钢管环径;对K2产生影响的因素有钢管壁厚、钢管管径、钢管环径;对T0产生影响的因素有铝套筒长度、预紧力大小、钢管壁厚、钢管管径。根据不同影响因素对应不同的参数取值，拟合出参数近似表达式，即

K1=15.482B1.104 6T1.519 8D-1.726 1， （6）

K2=345.537B1.120 3T0.455 3D-1.844 3， （7）

T0=0.006 48B1.122 3T1.537 9L0.240 8F0.185 9。 （8）

已知减压环尺寸，通过公式（6）～（8）可近似绘制出减压环的力-位移曲线。

5 结论

根据“等能量”原则，结合减压环的受力特点，提出了一套系统的减压环力-位移曲线的简化拟合方法。考虑到材料非线性和几何非线性的影响，通过数值模拟方法研究了减压环力-位移关系简化曲线参数的变化规律，得到了以下结论：

（1） 钢管的尺寸对减压环的力学性能影响较为明显。增加钢管的壁厚、管径均可明显增加减压环的刚度与耗能;增加钢管环径会降低减压环刚度，但同时也增加了减压环拉伸过程，在这两个因素影响下减压环的耗能存在极值。

（2） 铝套筒长度和厚度影响套筒与钢管之间的摩擦，进而影响减压环屈服强度，但对减压环的刚度影响不大。铝套筒的厚度应满足一定需求，否则铝套筒容易发生破坏，使减压环耗能性能大幅降低。

参考文献：

［1］ EOTA.Guideline for the European technical approval of falling rock protection kits［S］：European Organization for Technical Approvals，2013.

［2］ CASTANON-JANO L，BLANCO-FERNANDEZ E，CASTRO-FRESNO D，et al.Energy dissipating devices in falling rock protection barriers［J］.Rock Mechanics and Rock Engineering，2016（50）：603-619.

［3］ 赵世春，余志祥，赵雷，等.被动防护网系统强冲击作用下的传力破坏机制［J］.工程力学，2016，33（10）：24-34.

［4］ 柳春.柔性防护结构坡面地质灾害作用的离散化分析理论与方法［D］.成都：西南交通大学，2020.

［5］ CASTRO-FRESNO D，DAZ J D C J，NIETO J G P，et al.Comparative analysis of mechanical tensile tests and the explicit simulation of a brake energy dissipater by FEM［J］.International Journal of Nonlinear Sciences amp; Numerical Simulation，2009，10（8）：1059-1085.

［6］ GENTILINI C，GOTTARDI G，GOVONI L，et al.Design of falling rock protection barriers using numerical models［J］.Engineering Structures，2013（50）：96-106.

［7］ 汪敏，石少卿，阳友奎.减压环耗能性能的静力试验及动力有限元分析［J］.振动与冲击，2011，30（4）：188-193.

［8］ 刘成清，陈林雅，陈驰，等.被动柔性防护网中减压环力学试验及有限元分析［J］.岩石力学与工程学报，2016，35（6）：1245-1254.

［9］ 赵雅娜，余志祥，赵世春.多跨布置式环网柔性被动网结构数值计算方法［J］.振动与冲击，2019，38（17）：211-219.

［10］ 齐欣，许浒，余志祥，等.柔性拦截结构中减压环动态力学性能试验研究［J］.工程力学，2018，35（9）：188-196.

［11］ 黄俊飞.减压环腐蚀对柔性防护网系统力学性能影响［D］.成都：西南交通大学，2020.

［12］ 邓永祥.被动柔性防护网结构耗能器力学性能研究［D］.成都：西南交通大学，2017.

［13］ 向亮，陈艳，戴兰宏.轴向加载下不同捻向多股钢丝绳的力学行为研究［J］.应用力学学报，2023，40（5）：1025-1033.

［14］ 田芳，刘财喜，刘芳，等.Q235钢真实应力-应变曲线研究［J］.中南林业科技大学学报，2011，31（4）：182-186.

［15］ 张文帅，郭荣鑫，林志伟，等.加载应变速率对UHTCC薄板弯曲性能影响试验研究［J］.应用力学学报，2021，38（2）：523-529.

［16］ DAZ J D C J，NIETO J G P，CASTRO-FRESNO D，et al.Nonlinear explicit analysis and study of the behaviour of a new ring-type brake energy dissipator by FEM and experimental comparison［J］.Applied Mathematics and Computation，2010，216（5）：1571-1582.

［17］ TRAD A，LIMAM C，BERTRAND D，et al.Full-scale dynamic analysis of an innovative rockfall fence under impact using the discrete element method：from the local scale to the structure scale［J］.Rock Mechanics and Rock Engineering，2012，45（5）：885-900.

［18］ 赵雅娜.多跨布置式柔性被动网结构的关键构件及整体变形耗能性能分析［D］.成都：西南交通大学，2018.

Study on mechanical properties of ring-brake energy

dissipaters in passive flexible protection systems

AI Qinghua，WANG Yiming

（State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures，

Shijiazhuang Tiedao University，Shijiazhuang 050043，China）

Abstract

The ring-brake energy dissipaters is an important energy-dissipating device in the passive flexible protection system，and the in-depth study of the force-displacement relationship of the ring-brake energy dissipaters is of great significance for the design and the performance of the passive flexible protection system.Based on the principle of \"equal energy\"，this paper proposes a method of bi-polyline simplified model of ring-brake energy dissipaters force-displacement relation.Considering the influence of material nonlinearity and geometric nonlinearity，the finite element model of the ring-brake energy dissipaters was established by LS-DYNA software，the mechanical process of tensioning of the ring-brake energy dissipaters under dynamic load was simulated，and the sensitivity of the steel pipe wall thickness，steel pipe diameter，steel pipe ring diameter，aluminum sleeve length，aluminum sleeve thickness and preload to the parameters of the double polygonal model was studied，and the fitting formula of the three parameters was given.The results show that changing the wall thickness，pipe diameter or ring diameter of the steel pipe will effectively change the stiffness of the ring-brake energy dissipaters，and then have a great impact on the force-displacement curve of the ring-brake energy dissipaters，and changing the length or thickness of the aluminum sleeve will have little effect on the force-displacement curve of the ring-brake energy dissipaters，but if the aluminum sleeve thickness is too small it will easily lead to tearing damage of the sleeve.

Key words

Ring-brake energy dissipaters;Numerical simulation;Force-displacement curves;Simplify fitting parameters;Energy dissipation

（本文责编：葛 文）