基于自适应灰色区间模型的短时交通流不确定预测

摘要

为了更好地捕捉交通流随机波动的不确定性，提升短时交通流预测的准确性，进而为交通管理提供科学依据，提出一种自适应灰色区间模型，用于短时交通流的不确定预测。该自适应灰色区间模型由自适应灰色模型、粒子群算法和残差模型组成。首先，构建自适应灰色模型，预测短时交通流的均值，采用粒子群优化算法来实时获取自适应灰色模型的最优参数;然后，通过比较均值预测结果与真实值，得到残差序列，并对得到的残差序列进行绝对值处理，采用残差模型对经过绝对值处理的残差序列进行处理;最后，将均值预测结果与残差结果相结合，生成预测区间，实现对短时交通流的不确定量化。利用美国明尼苏达州高速公路采集的交通流数据对所提模型的性能进行评价，选择预测区间覆盖概率、预测区间宽度和综合指数作为不确定预测性能评价指标，并与灰色包络模型（GEPM）、灰色区间预测模型（GIPM）和线性灰色区间模型（LGIM）进行比较。结果表明，本文模型能够生成可行的交通流预测区间，通过比较不确定预测性能评价指标，表明本文模型有更好的预测精度，可以为智能交通系统提供决策支持。

关键词

智能交通;短时交通流预测;不确定预测;自适应灰色区间模型;粒子群优化

中图分类号：U491.1"" 文献标志码：A"" 文章编号：1004-0366（2024）06-0114-07

随着私家车数量和出行需求的不断增加，城市交通拥堵问题日趋严重［1］。为有效缓解这一问题，学者们相继提出各种缓解交通拥堵的策略方案。其中，智能交通系统成为缓解交通拥堵的主要手段之一，也成为当前研究的热点［2］。短时交通流预测作为智能交通系统的关键输入，是该研究的重点。

既有文献对短时交通流的预测多为均值预测［3］，根据一系列历史数据直接预测出交通流的平均值，但交通流预测的精度往往受到天气、事件、驾驶员行为等多种不确定因素的影响，因此需要提出一种能够实现对短时交通流不确定性预测的方法［4］。短时交通流不确定性预测是在均值预测的基础上生成一个区间，通常称为预测区间［2，5］，精确的预测区间能够在智能交通系统领域实现更可靠的应用，如出行者可以根据交通状况的上限和下限做出更优的出行选择［5］，管理者可以了解所做决策带来的最佳和最坏结果，从而制定对应的政策［6］。

目前，关于短时交通流不确定预测的文献较少，常见的方法主要包括随机波动模型（stochastic volatility model）［7-8］、广义自回归条件异方差（GARCH，generalized autoregressive conditional heteroscedasticity）模型［9］和Bootstrap模型［10］等。值得注意的是，这些不确定预测方法对数据样本量有较高的要求。然而，在某些国家和地区因采集设备故障或数据库受损，无法获取足够的数据，使得这些方法并不适用［11］。

DENG［12］提出的灰色模型在数据较少的情况下能够有效预测短时交通流的不确定性，如灰色包络模型（GEPM）［13］、灰色区间预测模型（GIPM）［14］和线性灰色区间模型（LGIM）［15］。上述灰色模型的核心在于构建区间数据序列，但大多数方法将原始数据划分为上限和下限序列，在白化过程中可能导致信息丢失，从而影响短时交通流不确定预测的精度［16］。交通流具有实时动态变化的特点，而上述灰色模型多是离线模型，无法根据实时数据进行调整，难以适应交通流的瞬时波动。这使得上述模型在应对实际的交通流预测时存在局限性，无法提供及时、准确的预测结果。

因此，本文提出一种自适应灰色区间模型，实现对短时交通流的实时不确定预测。该模型由自适应灰色模型、粒子群算法和残差模型组成，由自适应灰色模型预测短时交通流的均值，再由残差模型预测短时交通流均值的残差，通过均值与残差的结合生成预测区间，实现对短时交通流的不确定量化。以美国明尼苏达州高速公路交通流数据为实验数据，通过区间预测性能评价指标来验证本文模型的不确定预测性能。

1 "研究方法

本文提出一种基于自适应灰色区间模型的短时交通流不确定预测框架，该框架内容由自适应灰色模型、粒子群优化算法以及灰色残差模型组成。

1.1 自适应灰色模型

自适应灰色模型是在传统灰色模型基础上引入了自适应的机制，其模型如下：

设t时刻数据序列为Xt=［x（t-T+1），…，x（t-1），x（t）］，其中T为时间窗口，通过敏感性分析得到。采用一阶累加生成算子（1-AGO，1-accumulating generation operator）来生成Xt的一次累加序列Yt，即

Yt（i）=∑ij=1Xt（j）， i=1，2，…，n （1）

再生成Xt序列的紧邻生成序列，称为背景值序列Zt，即

Zt（i）=αYt（i）+（1-α）Yt（i）， （2）

其中：α为权重系数，一般取0.5。

累加序列Yt可将随机波动序列Xt转换为具有单调特征的序列，所以可以建立Xt与Yt之间的关系，这种灰色预测模型的基本结构为

Xt（i）+aYt（i）=b。 （3）

DENG［12］发现式（3）预测结果存在较大误差，故采用背景值序列Zt代替Yt对式（3）进行改进，即

Xt（i）+aZt（i）=b， （4）

其中：a为灰色预测模型的发展系数;b为灰色预测模型的灰作用量。

将求得的参数a、b代入式（4）中，可得对应的白化微分方程的解为

t（i）=Xt（1）-bae-a（i-1）+ba， i=1，2，…（5）

其中：参数a、b可以通过粒子群优化算法得到。

由一阶累减还原算子累减还原后，得到原始数据的预测值为

Yt（1）=Xt（1），i=1

t（i）=Yt（i）-Yt（i-1），i=2，3，…（6）

其中：t（i）表示预测的累加序列;t（i）表示通过累减还原得到的预测序列。

1.2 粒子群优化算法

对于t时刻灰色模型，有a、b两个参数需要优化，以满足交通状况实时变化的特征。本文提出的自适应灰色模型本质上是自适应的，自适应机制采用粒子群优化（PSO，particle swarm optimization）方法寻找t时刻的最优参数实现。PSO通过模拟多个个体（即粒子）在搜索空间中的运动来找到最优解。每个粒子代表一个潜在的解决方案，粒子通过跟踪自己历史上的最优位置以及群体中最优位置来调整自己的速度和位置。粒子在不断迭代的过程中趋向于最优解，此过程包括4个步骤：种群初始化、目标函数计算、粒子速度和位置更新、优化参数输出。其优化过程说明如下：

（1） 种群初始化。在搜索空间中随机生成多个粒子，每个粒子都有一个位置向量和速度向量。位置向量表示待优化的两个参数（a和b）的信息，代表一个潜在解；速度向量表示在下一轮迭代中移动的方向和距离。粒子的初始位置和速度通常是随机设置的。由于待优化参数的个数为2，因此搜索维度设置为2，种群规模设置为200。

（2） 目标函数计算。每个粒子代表一个解，对应一个灰色模型，将训练样本输入该灰色模型得到相应的输出值，通过与真实值比较得到误差作为目标函数，目标函数公式为

MSE=1p∑pi=1（Xt（i）-t（i））， （7）

其中：Xt（i）为t时刻的真实值;t（i）为通过灰色模型得到的t时刻的预测值;p为训练样本个数。

（3） 粒子速度和位置更新。比较当前粒子适应值与上一次迭代的适应值，若当前粒子适应值更优，则按照公式

vk+1i，j=wvk+1i，j+l1rand（pki，j，pbest-pki，j）+l2rand（gkj，pbest-pki，j），（8）

pk+1i，j=pki，j+vk+1i，j （9）

进行粒子速度和位置的更新，其中：vk+1i，j为粒子i在第j维第k+1迭代的初始速度;pk+1i，j为粒子i在第j维第k+1的初始位置;j=2为搜索维度;w为（0.4，2）之间的惯性权重;rand（.）为（0，1）之间的随机数;l1为（0，4）之间的自学习因子;l2为（0，4）之间的群学习因子。本文中w取0.8，l1和l2取1.5。

（4） 优化参数输出。

设定最大迭代次数为50次，优化过程中重复步骤（2）～（3），直至达到最大迭代次数，优化过程停止后，确定最优的解a和b。

1.3 残差模型

自适应灰色模型得到预测序列后，再与真实值进行比较，得到残差序列εt（i），即

1.4 "整体框架

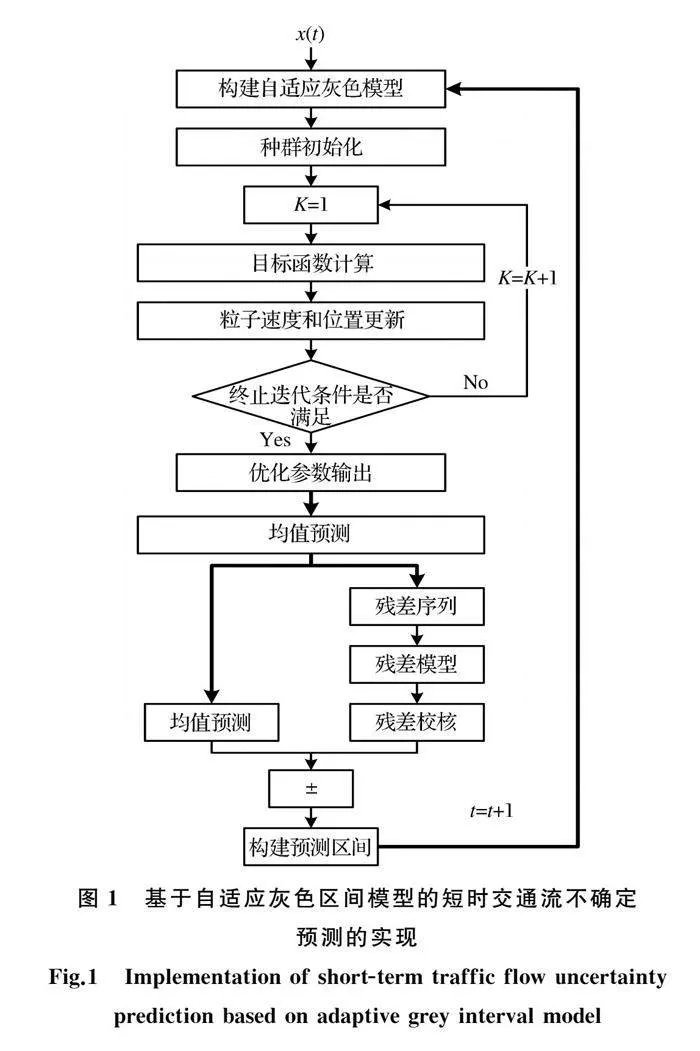
基于自适应灰色区间模型的短时交通流不确定预测的实现过程如图1所示，按照以下步骤开展短时交通流的不确定预测：

步骤1 构建自适应灰色模型;

步骤2 用粒子群优化算法获得自适应灰色模型的最优系数;

步骤3 基于最优系数的自适应灰色模型进行均值预测;

步骤4 比较均值预测结果和真实值，生成残差序列，并对残差序列进行绝对值处理;

步骤5 基于取绝对值后的残差序列，构建残差模型;

步骤6 将均值预测结果和残差校核结果相结合生成预测区间，实现对短时交通流的不确定预测。

本文模型具有自适应性，即根据输入交通数据序列的不同自适应调整模型的结构，从而完成交通流实时不确定预测。首先利用输入的交通数据序列更新模型，然后基于更新后的模型生成预测值，即在完成t时刻的均值预测后，生成t时刻的残差序列，获得t时刻的不确定预测结果（预测区间），再将t+1时刻的观测交通流数据滚入原交通流数据序列中，并移除原交通流数据序列中最早的交通流数据，从而形成更新后的交通流数据序列，即t+1时刻的新交通流数据序列。由t+1时刻的新交通流数据序列构建t+1时刻的模型结构，并完成t+1时刻的均值预测、t+1时刻的残差序列，从而生成t+1时刻的不确定预测结果（预测区间）。以此方式实现模型的自适应，并完成短时交通流的实时不确定预测。

2 实例分析

2.1 "研究对象

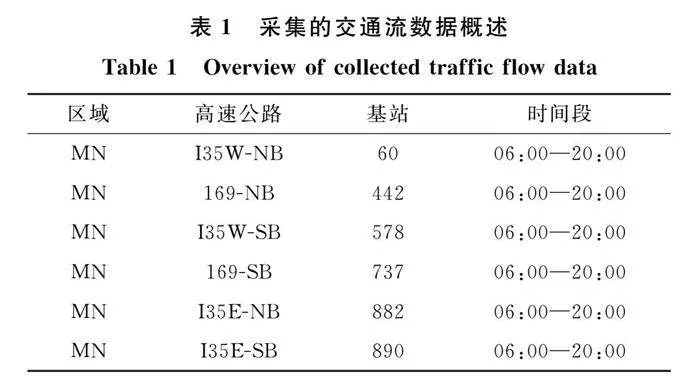
从美国明尼苏达州高速公路系统中选择6个基站（60，578，882，890，442，737）的交通数据来验证本文模型的区间预测性能。所选时段为2019年6月18日06：00—20：00，采集间隔为15 min，其交通流数据概览如表1所列。

2.2 评价标准

为了更好地验证本文模型的预测性能，选择GEPM［13］、GIPM［14］和LGIM［15］作为比较模型。不同于以往短时交通流均值预测性能评价，本次研究的目的是以预测区间的形式来量化短时交通流的不确定性，因此，需要选择预测区间的评价指标来评估短时交通流不确定预测的性能。基于已有文献［2，11，17］中关于短时交通流不确定预测评价指标的研究，选择3个性能指标来评估预测区间的性能，即预测区间覆盖概率（PICP）、平均宽度区间（WI）、指数P［11，17］。PICP的计算方法是落入预测区间内的实际观测值的数量除以实际观测值的样本量。PICP预计没有原始真实值会落在预测区间之外。平均WI 是预测区间的平均带宽，窄WI比宽WI更具信息量。理想情况下，当PICP较大且平均WI较窄时，我们期望预测区间更好。因此，采用综合衡量指标P来评估区间预测性能。3个指标的计算公式如下：

PICP=1n∑ni=1ci， （17）

ci=1，lowilt;xilt;upi

0，lowigt;xiorxigt;upi （18）

WI=1n∑ni=1（upi-lowi）， （19）

P=2×PICP×1WIPICP+1WI， （20）

其中：xi为原始真实值;lowi为预测下限;upi为预测上限;n为原始真实值的总数。理想情况下，PICP期望没有原始真实值会落在预测区间之外，窄WI比宽 WI更具信息量，而P值越高意味着测试模型越有效。

2.3 不确定预测结果

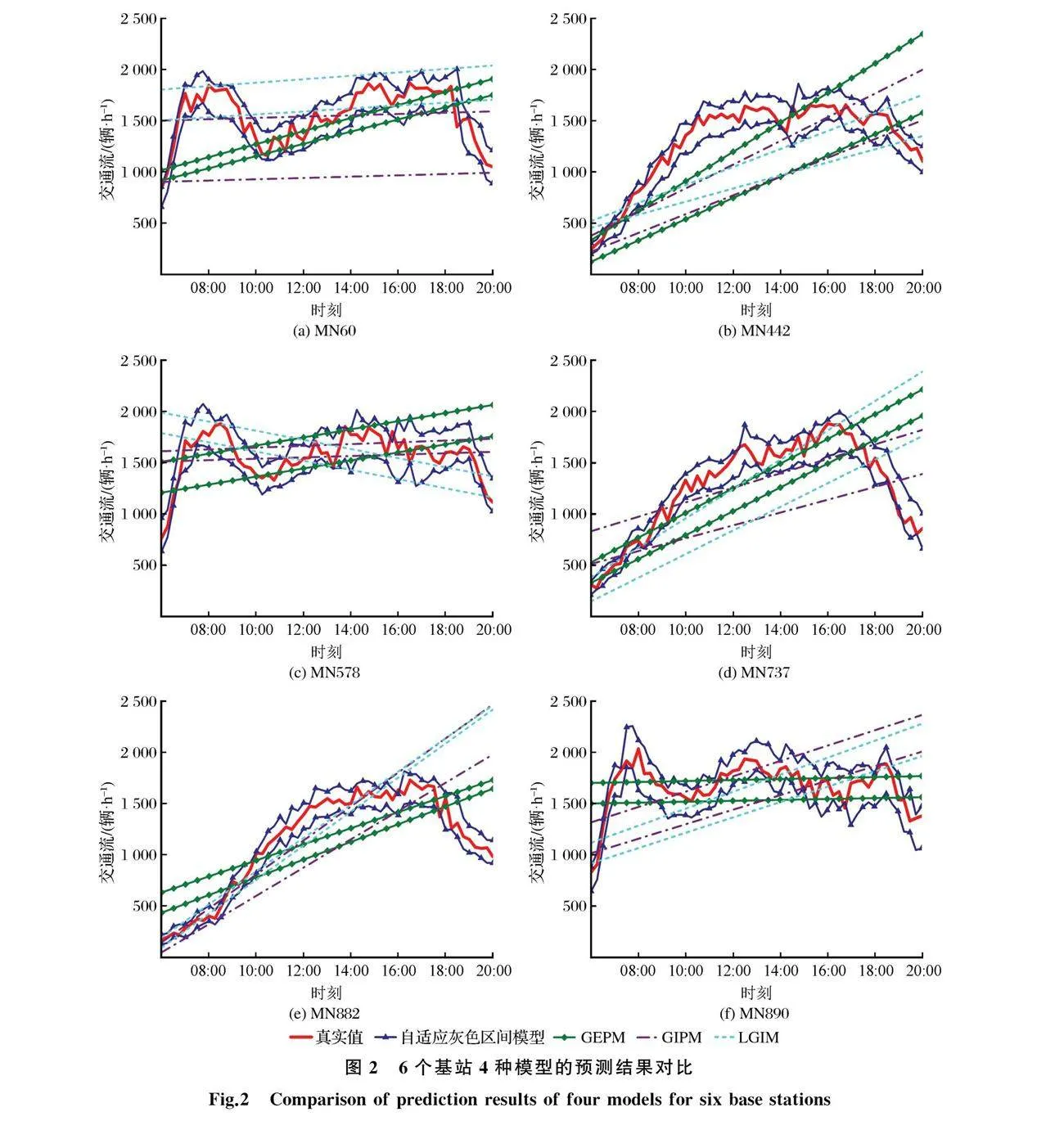
06：00—20：00时间段6个基站4种不同模型的短时交通流的预测区间如图2所示。由图2可知，4种模型均能生成可行的预测区间，说明提出自适应灰色区间模型能够有效量化短时交通流的不确定性；GEPM、GIPM和LGIM的区间预测结果呈现单调递增或递减的特性，但不能反映车速数据序列的随机振荡趋势，对交通流预测区间效果不佳；自适应灰色区间模型可以跟踪现场实测交通流的变化趋势，说明本文模型对交通流数据进行不确定预测的结果能更好地捕捉交通流数据在不同时刻的波动特征。

2.4 不确定预测性能分析

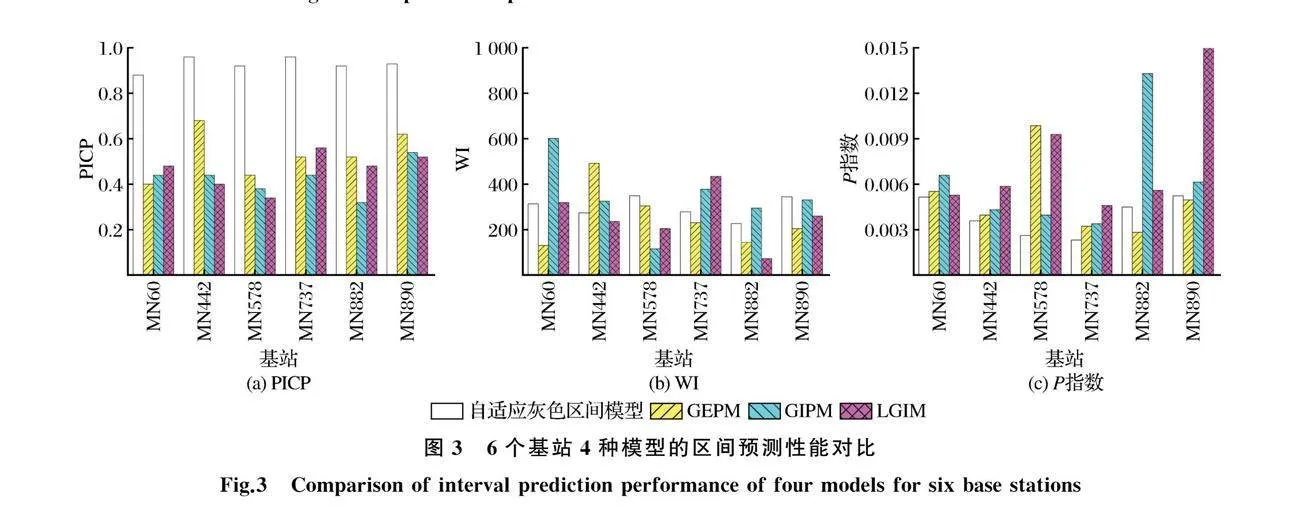
为进一步调查自适应灰色区间预测模型在短时交通流不确定预测方面的性能，运用3个性能指标（PICP、WI和P指数）来衡量模型性能，如图3所示。由图3（a）可知，本文模型的 PICPgt;80%，在每个基站都明显大于比较模型GEPM、GIPM和LGIM的 PICP，但从图3（b）的WI值可以看出，GEPM、GIPM和LGIM 模型的WI值较小，所以其预测效果要优于本文模型，这是因为区间宽度越大，交通流落在预测区间的概率越大，则覆盖率越大。虽然本文模型的WI值比其他3个模型大，但是本文模型的PICP值却优于其他3个模型。因此，为了清楚地说明不同模型预测区间的性能，根据式（20）计算综合指数P来进一步判断本文模型的性能水平［见图3（c）］。图3（c）显示本文模型的P值是

4个模型中最小的，对于这6个基站，本文模型的表现均优于其他3个模型，说明本文模型估计的预测区间具有更好的性能。综合考虑4个区间预测模型（GEPM、GIPM、LGIM和自适应灰色区间模型）的性能指标结果，发现自适应灰色区间模型的区间预测结果性能最优。

3 结论

考虑到短时交通流预测的准确性受到天气、事故和驾驶员行为等各种不确定因素的影响，提出自适应灰色区间模型用于预测短时交通流的不确定性，得到的预测区间能更准确地反映这些不确定特征，提高了预测的准确性。采用美国明尼苏达州高速公路采集的真实交通流数据，使用3个性能指标（PICP、WI和P指数），并与GEPM、GIPM和LGIM进行比较，以评价本文模型的有效性。研究得出以下结论：

（1） 本文模型的性能优于其他模型，表明利用本文模型估计预测区间可以获得覆盖率更高、区间带宽更窄的高质量预测区间，更有利于短时交通流的区间建模。

（2） 本文模型可以跟踪现场实测交通流的变化趋势，说明本文模型对交通流数据进行不确定预测的结果能更好地捕捉交通流数据随不同时刻的波动特征。

（3） 本文模型生成的预测区间可以有效应用于智能交通系统，可在提升交通管理的智能化水平、优化出行体验、提高公共交通服务效率等方面广泛应用。尤其在高峰时段，面对复杂、多变的交通环境时，区间预测结果能够更有效应对不确定性，为交通系统的高效运行提供决策支持。

参考文献：

［1］ 张俊溪，曲仕茹，张志腾，等.时空相关的道路网络短时交通流预测模型［J］.北京交通大学学报，2024，48（3）：74-82.

［2］ LI M，FANG L，JIA W W，et al，Traffic condition uncertainty quantification under nonnormal distributions［J］.Journal of Transportation Engineering，2022，148（10）：1-14.

［3］ 李秀丽，李星毅.多断面相关性区间预测法在短期交通流预测中的应用［J］.电子设计工程，2017，25（19）：10-15.

［4］ 李丹华，秦涛，张为.高速公路区间交通态势预测系统设计［J］.中国交通信息化，2022，266（2）：119-122.

［5］ WANG Y P，KE S P，AN C C，et al.A hybrid framework combining LSTM NN and BNN for short-term traffic flow prediction and uncertainty quantification［J］.KSCE Journal of Civil Engineering，2023，28（1）：363-374.

［6］ LI Y，CHAI S，WANG G，et al.Quantifying the uncertainty in long-term traffic prediction based on PI-ConvLSTM network［J］.IEEE Transactions on Intelligent Transportation Systems，2022，23（11）：20429-20441.

［7］ TSEKERIS T，STATHOPOULOS A.Short-term prediction of urban traffic variability：stochastic volatility modeling approach［J］.Journal of Transportation Engineering，2010，136（7）：606-613.

［8］ ZHANG Y R，HAGHANI A，SUN R Y.Stochastic volatility modeling approach that accounts for uncertainties in travel time reliability forecasting［J］.Transportation Research Record，2014，2442（1）：62-70.

［9］ 王晓全，邵春福，尹超英，等.基于ARIMA-GARCH-M模型的短时交通流预测方法［J］.北京交通大学学报，2018，42（4）：79-84.

［10］ NAIK B，RILETT L R，APPIAH J，et al.Resampling methods for estimating travel time uncertainty：application of the gap bootstrap［J］.Transportation Research Record，2018，2672（42）：137-147.

［11］ SONG Z G，FENG W，LIU W W.Interval prediction of short-term traffic speed with limited data input：application of fuzzy-grey combined prediction model［J］.Expert System Application，2022（187）：115878.

［12］ DENG J L.Introduction to grey system theory［J］.Journal of Grey System，1989，1（1）：1-24.

［13］ 肖代全，马荣国.交通量的灰包络预测［J］.交通科技与经济，2005，32（6）：53-55.

［14］ CHEN Y Y，LIU H T，HSIEH H L.Time series interval forecast using GM（1，1） and NGBM（1，1） models［J］.Soft Computing，2019，23（5）：1541-1555.

［15］ HUANG Y，LIN C.Developing an interval forecasting method to predict undulated demand［J］.Quality Quantity，2011，45（3）：513-524.

［16］ WU W Z，ZHANG T.An improved gray interval forecast method and its application［J］.Communications in Statistics-Theory and Methods，2020，49（5）：1120-1131.

［17］ YUAN X H，CHEN C，JIANG M，et al，Prediction interval of wind power using parameter optimized Beta distribution based LSTM model［J］.Applied Soft Computing Journal，2019（82）：105550.

Uncertainty prediction of short-term traffic flow

based on adaptive grey interval model

LI Hao

（Civil Engineering College，Shaanxi Polytechnic Institute，Xianyang 712000，China）

Abstract

In order to better capture the uncertainty of random fluctuations in traffic flow and improve the accuracy of short-term traffic flow prediction，an adaptive grey interval model is proposed in this paper for uncertain prediction of short-term traffic flow.The adaptive grey interval model consists of an adaptive grey model，a particle swarm optimization algorithm and a residual model.First，an adaptive grey model is constructed to predict the mean of short-term traffic flow.The particle swarm optimization algorithm is used to obtain the optimal parameters of the adaptive grey model in real time.Then，the residual sequence is obtained by comparing the mean prediction result with the true value，the obtained residual sequence is processed by absolute value，and the residual model is used to process the residual sequence processed by absolute value.Finally，the mean prediction result is combined with the residual result to generate a prediction interval to realize the uncertainty quantification of short-term traffic flow.The performance of the proposed model is evaluated using traffic flow data collected from highways in Minnesota，USA.The prediction interval coverage probability，prediction interval width and comprehensive index are selected as uncertainty prediction performance evaluation indicators，and compared with the grey envelope model （GEPM），grey interval prediction model （GIPM） and linear grey interval model （LGIM）.The results show that the proposed model can generate feasible traffic flow prediction intervals.By comparing the uncertain prediction performance evaluation indicators，it is shown that the proposed model has better prediction accuracy and can provide decision support for intelligent transportation systems.

Key words

Intelligent transportation system;Short-term traffic prediction;Uncertainty prediction;Adaptive grey interval model;Particle swarm optimization

（本文责编：冯 婷）