LTNE条件下多孔方腔内Cu-水纳米流体自然对流研究

摘要

采用局部非热平衡假设，对固体骨架分别为玻璃球和泡沫铝的多孔介质方腔内Cu-水纳米流体自然对流进行数值模拟。研究了无量纲容积换热系数、瑞利数、孔隙率和纳米颗粒体积分数对多孔方腔内纳米流体自然对流传热特性的影响。结果表明，当瑞利数较小时，可以用局部热平衡模型代替局部非热平衡模型计算多孔腔体内的自然对流。当瑞利数较大时，对于填充玻璃球的多孔腔体自然对流，孔隙率较大时可以采用局部热平衡模型计算，而对于填充泡沫铝的多孔腔体自然对流应采用局部非热平衡模型计算。填充泡沫铝的腔体内使用Cu-水纳米流体时，总的传热速率并没有明显的变化。对于填充玻璃球的腔体，当瑞利数较小时使用Cu-水纳米流体可以明显增加腔体的传热速率，而当瑞利数较大时填充玻璃球的腔体传热速率随纳米颗粒体积分数的增大而降低。

关键词

纳米流体;多孔介质;自然对流;局部非热平衡

中图分类号：TK124"" 文献标志码：A"" 文章编号：1004-0366（2024）06-0137-07

多孔介质内的传热可以用局部热平衡（LTE，local thermal equilibrium）模型和局部非热平衡（LTNE，local thermal non-equilibrium）模型进行描述，与LTE模型相比，LTNE模型考虑了流体和固体骨架之间的热量传输。对于大多数多孔介质内流动传热的研究，通常都假定构成多孔介质的固体骨架和流体满足LTE假设，对含水层或油气储层进行传热现象建模通常采用这种方法。然而，有时多孔介质中的固体骨架和流体之间的温差不可忽略，LTE假设可能不适用于核反应堆、高导热性泡沫金属和电子设备内的流动传热现象［1］。

与传统流体水和油相比，纳米流体具有更高的导热系数［2］。多孔介质腔体内的纳米流体自然对流在电子元器件冷却［3］、太阳能发电厂［4］、蓄热系统［5］等领域中有着潜在的应用价值。许多学者对LTNE条件下多孔腔体内纳米流体的自然对流进行了研究，如SIDDHESHWAR等［6］研究了LTNE条件下多孔介质腔体内Cu-水纳米流体的自然对流，结果表明，固体骨架与纳米液体的导热系数接近时LTE模型是可以使用的;IZADI等［7］首次采用LTNE模型和微极流动理论数值研究了多孔介质方腔内CuO-水纳米流体的自然对流，其结果表明，随着孔隙率的增大，微旋转的强度降低，微极性流动转变为典型流动；MEHRYAN等［8］采用LTNE模型数值研究了多孔方腔内混合纳米流体的自然对流，其结果表明，使用纳米流体降低了固相和液相的传热速率，同时削弱了LTNE效应；SIVASANKARAN等［5］采用LTNE模型数值研究了倾斜多孔介质方腔中Cu-水纳米流体的自然对流；TAYEBI等［9］采用LTNE模型数值研究了Cu-水纳米流体在多孔圆环中的自然对流。

综上所述，当固体骨架和液相间存在温差时，会导致多孔介质不满足LTE假设，并且涉及自然对流的许多工程中都存在非均匀加热或冷却的热边界条件。因此，对固体骨架分别为玻璃球和泡沫铝的多孔方腔内Cu-水纳米流体自然对流传热进行数值研究，其中方腔热壁面为正弦温度边界条件，分析了LTNE条件下无量纲容积换热系数Nhs、瑞利数Ra、孔隙率ε和纳米颗粒体积分数φ对传热特性的影响。

1 物理问题描述及数值方法

充满饱和多孔介质的方腔如图1所示。方腔左侧壁面保持正弦温度分布T=Tc+（Th-Tc）sin（πy/L），右侧壁面保持低温Tc，上下壁面绝热，同时壁面不可渗透且无滑移。以玻璃球（ks=1.05 W·m-1·K-1）、铝金属泡沫（ks=205 W·m-1·K-1）作为多孔介质固体骨架。腔体内工作流体为Cu-水纳米流体，Cu纳米颗粒的直径为25 nm。计算中所涉及的水和Cu纳米颗粒的热物性参数［5，10］如表1所列。纳米流体的热物性参数按照表2所列的公式计算［11-12］。Tfr是基液的冰点温度，ReB和uB分别是纳米颗粒布朗运动雷诺数和纳米颗粒布朗运动速度，定义为［11］

ReB=ρfuBdnpμf，uB=2kbTπμfd2np， （1）

其中：dnp为Cu纳米颗粒的直径（m）;kb为玻尔兹曼常数，kb=1.38×10-23 J/K;参数的下标np、nf和f分别表示纳米颗粒、纳米流体和基液。

充满纳米流体的多孔介质的有效导热系数以及热扩散系数为

kmnf=εknf+（1-ε）ks，αmnf=kmnf/（ρcp）nf，（2）

其中：参数下标mnf和s分别代表充满纳米流体的多孔介质和多孔介质固体骨架。

假设流体与固体骨架温度不等，腔体内的流动为层流，且流体为不可压缩的Cu-水纳米流体，忽略黏性耗散的影响。同时引入Boussinesq假设考虑自然对流效应。对于LTNE条件下多孔介质方腔内Cu-水纳米流体的二维稳态层流自然对流，无量纲控制方程［9，13］为

UX+VY=0， （3）

1ε2UUX+VUY=-PX+νnfPrνfε2UX2+2UY2-νnfPrνfDaU-CFDaU2+V2U， （4）

1ε2UVX+VVY=-PY+νnfPrνfε2VX2+2VY2-νnfPrνfDaV-CFDaU2+V2V+βnfβfRaPrθnf， （5）

1εUθnfX+VθnfY=knfkf（ρcp）f（ρcp）nf2θnfX2+2θnfY2+（ρcp）f（ρcp）nfNhs（θs-θnf），（6）

0=2θsX2+2θsY2+γNhs（θnf-θs）， （7）

涉及的无量纲量如下：

X=xL，Y=yL，U=uLαf，V=vLαf，Pr=νfαf，

P=pρnf（αf/L）2，θ=T-TcTh-Tc，Nhs=hL2εkf，

Ra=gβf（Th-Tc）L3νfαf，Da=KL2，γ=εkf（1-ε）ks，（8）

其中：U、V分别为X、Y方向的无量纲速度;g为重力加速度（m/s2）;K为多孔介质渗透率（m2）;ε为孔隙率;h为容积换热系数［W/（m2·K）］;CF为惯性系数，其计算式［14］为

CF=1.75150ε3。 （9）

边界条件为：

上下壁面：U=V=0，θs/Y=θnf/Y=0

左侧壁面：U=V=0，θnf=θs=sin（πY）

右侧壁面：U=V=0，θ=0。（10）

液相和固相在左侧壁面的局部努塞尔数Nunf及Nus定义为

Nunf=-knfkfθnfXX=0，Nus=-kskfθsXX=0。（11）

将固液两相局部努塞尔数加权得到左侧壁面总的局部努塞尔数Nu为

Nu=εNunf+（1-ε）Nus， （12）

总的平均努塞尔数Nu定义为

Nu=kmnfkf∫10-θXX=0dY。 （13）

为了分析使用纳米流体对传热的影响，引入Nu数比R：

R=NuNuφ=0。 （14）

采用SIMPLE算法对上述问题进行数值计算。为保证计算程序的可靠性，对文献［15］中LTNE条件下多孔方腔内纳米流体的自然对流问题进行数值模拟，结果如表3所列。Nunf及Nus与文献值吻合较好，表明所使用的程序是可靠的。同时发现当网格为100×100时，网格数的变化将不再对数值计算的结果造成影响，得到网格无关解。

2 结果分析与讨论

在Da=10-2的条件下，对正弦温度边界条件下固体骨架分别为玻璃球和铝金属泡沫的多孔介质方腔内Cu-水纳米流体自然对流传热进行了数值研究，分析了无量纲容积换热系数（Nhs=10～1 000）、Ra（Ra=103～105）、孔隙率（ε=0.1～0.9）和纳米颗粒体积分数（φ=0～0.04）对传热特性的影响。

图2为Ra=105、φ=0.01、ε=0.5及Nhs=10时，分别填充不同固体骨架的多孔介质方腔内的固液相温度场。填充不同类型固体骨架的多孔介质方腔内的固相温度场分布相似，如图2（a）和图2（c）所示。填充不同类型固体骨架的多孔介质方腔内的液相温度场分布也相似，如图2（b）和图2（d）所示。这是由于固相和液相间传热较为微弱，固相和液相温度场互相没有干扰导致的。

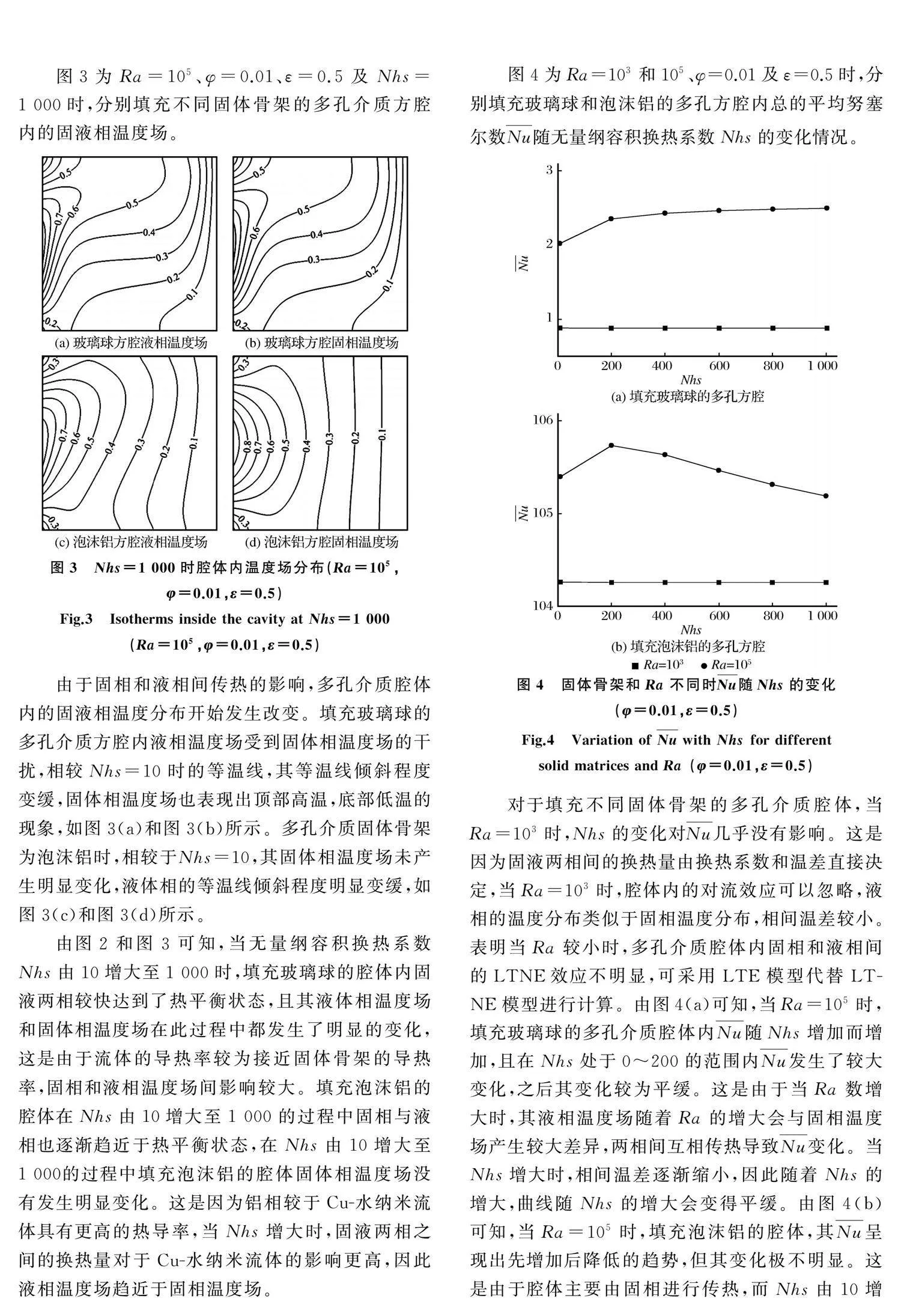
图3为Ra=105、φ=0.01、ε=0.5及Nhs=1 000时，分别填充不同固体骨架的多孔介质方腔内的固液相温度场。

由于固相和液相间传热的影响，多孔介质腔体内的固液相温度分布开始发生改变。填充玻璃球的多孔介质方腔内液相温度场受到固体相温度场的干扰，相较Nhs=10时的等温线，其等温线倾斜程度变缓，固体相温度场也表现出顶部高温，底部低温的现象，如图3（a）和图3（b）所示。多孔介质固体骨架为泡沫铝时，相较于Nhs=10，其固体相温度场未产生明显变化，液体相的等温线倾斜程度明显变缓，如图3（c）和图3（d）所示。

由图2和图3可知，当无量纲容积换热系数Nhs由10增大至1 000时，填充玻璃球的腔体内固液两相较快达到了热平衡状态，且其液体相温度场和固体相温度场在此过程中都发生了明显的变化，这是由于流体的导热率较为接近固体骨架的导热率，固相和液相温度场间影响较大。填充泡沫铝的腔体在Nhs由10增大至1 000的过程中固相与液相也逐渐趋近于热平衡状态，在Nhs由10增大至1 000的过程中填充泡沫铝的腔体固体相温度场没有发生明显变化。这是因为铝相较于Cu-水纳米流体具有更高的热导率，当Nhs增大时，固液两相之间的换热量对于Cu-水纳米流体的影响更高，因此液相温度场趋近于固相温度场。

图4为Ra=103和105、φ=0.01及ε=0.5时，分别填充玻璃球和泡沫铝的多孔方腔内总的平均努塞尔数Nu随无量纲容积换热系数Nhs的变化情况。

对于填充不同固体骨架的多孔介质腔体，当Ra=103时，Nhs的变化对Nu几乎没有影响。这是因为固液两相间的换热量由换热系数和温差直接决定，当Ra=103时，腔体内的对流效应可以忽略，液相的温度分布类似于固相温度分布，相间温差较小。表明当Ra较小时，多孔介质腔体内固相和液相间的LTNE效应不明显，可采用LTE模型代替LTNE模型进行计算。由图4（a）可知，当Ra=105时，填充玻璃球的多孔介质腔体内Nu随Nhs增加而增加，且在Nhs处于0～200的范围内Nu发生了较大变化，之后其变化较为平缓。这是由于当Ra数增大时，其液相温度场随着Ra的增大会与固相温度场产生较大差异，两相间互相传热导致Nu变化。当Nhs增大时，相间温差逐渐缩小，因此随着Nhs的增大，曲线随Nhs的增大会变得平缓。由图4（b）可知，当Ra=105时，填充泡沫铝的腔体，其Nu呈现出先增加后降低的趋势，但其变化极不明显。这是由于腔体主要由固相进行传热，而Nhs由10增大到1 000时，填充泡沫铝的腔体固相温度场几乎不发生变化。

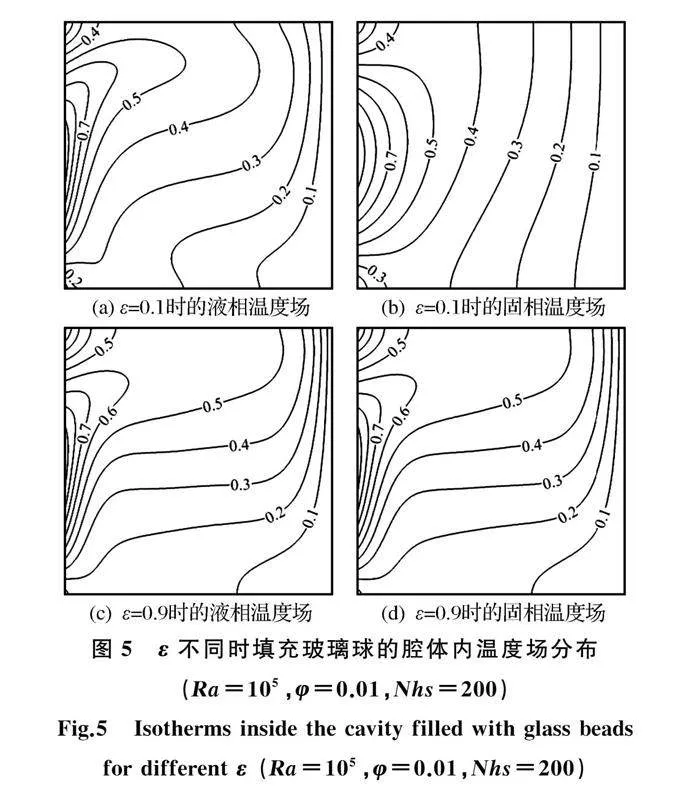
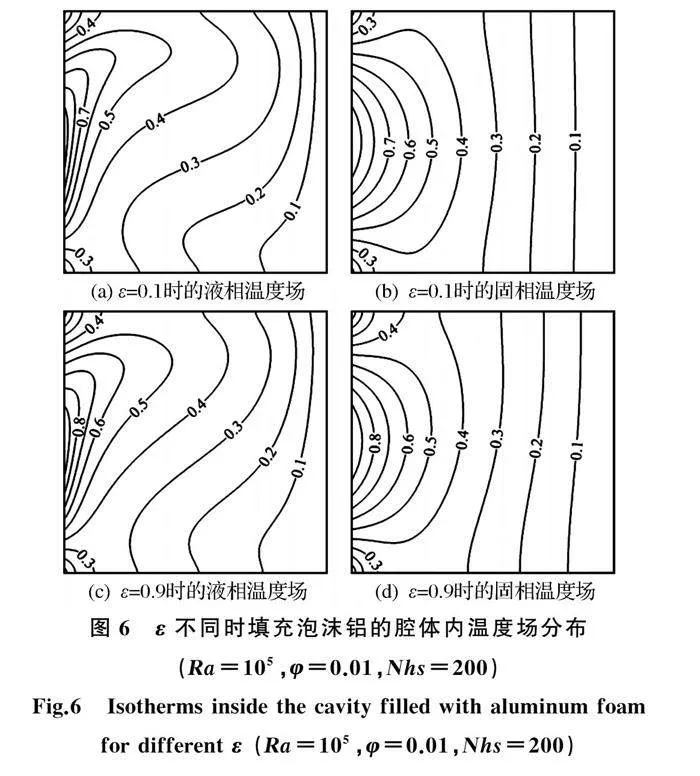
在Ra=105、φ=0.01、Nhs=200的条件下，腔体填充玻璃球和泡沫铝时，不同孔隙率ε下的固液相温度场如图5和图6所示。

由图5（a）和（c）可知，对于填充玻璃球的腔体，ε由0.1增大到0.9时，腔体中部的液相等温线趋近于水平方向。由图5（b）和（d）可知，随着ε的增大，固相温度场在腔体的右上角和左侧壁面附近形成了温度边界层，且腔体内的固相温度分布趋向于液相温度场。这意味着，当ε较低时，填充玻璃球的多孔介质腔体内固相和液相间的非热平衡效应较为明显，此时应考虑采用双能量方程模拟自然对流温度场。而当ε较大时，可以考虑采用热平衡模型计算自然对流。由图6（b）和（d）可知，对于填充泡沫铝的多孔介质腔体，当ε由0.1增大到0.9时，其固相温度场的变化较为微弱。如图6（c）和（d）可知，当ε增大到0.9时，固相温度场和液相温度场仍具有很大差异，表明对于填充泡沫铝多孔腔体，模拟自然对流时应采用LTNE模型。

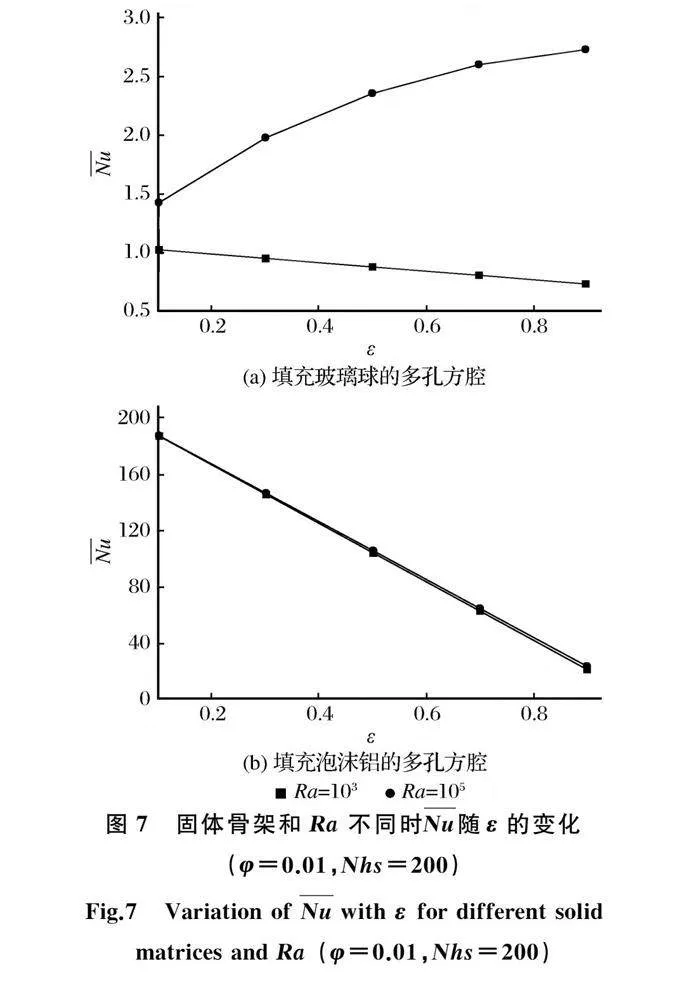
图7为Ra=103和105、φ=0.01、Nhs=200及固体骨架不同时方腔总的平均努塞尔数Nu随ε的变化情况。由图7（a）可知，对于填充玻璃球的多孔腔体，当Ra=103时，随ε的增加Nu减少，而Ra=105时ε的增大有利于传热。这是因为玻璃球的导热率接近Cu-水纳米流体，固相和液相传递的热量处于同一量级。当Ra数较大时，由于ε的增大增加了流体流通量，使得液相传热增加，抵消了固相传热的降低，因此总的传热量增大。由图7（b）可知，

对于填充泡沫铝的多孔腔体，增大ε严重降低了腔体的传热速率。这是因为泡沫铝具有较大的导热率，导致热壁面产生的热量主要由固相传递至冷壁面，而ε增大严重降低了固相的传热量，使得总的传热速率降低。

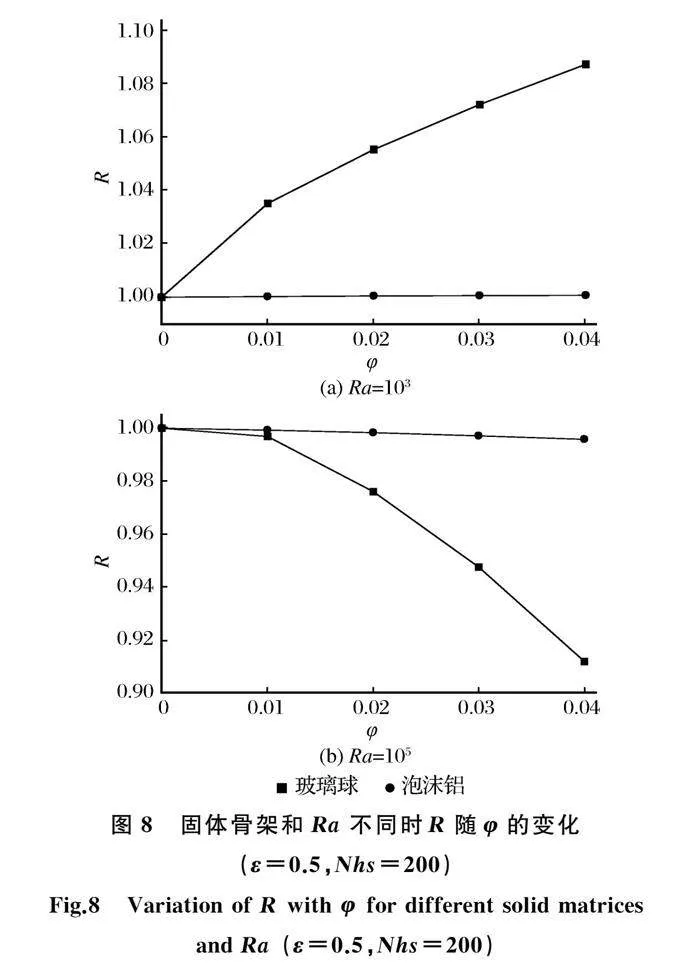
图8为Ra=103和105、ε=0.5、Nhs=200及固体骨架不同时的平均努塞尔数与流体为纯水时的平均努塞尔数之比R随φ的变化情况。

由图8（a）可知，当Ra=103时，对于固体骨架为玻璃球的多孔腔体，相较于纯水，使用Cu-水纳米流体明显增加了腔体的传热速率，在φ达到0.04时，同纯水相比腔体的传热速率增加了8.72%。而填充泡沫铝的腔体内使用Cu-水纳米流体，总的传热速率并没有明显的变化。由图8（b）可知，当Ra=105时，填充玻璃球的腔体传热速率随φ的增大而降低，当φ达到0.04时，腔体传热速率降低了8.80%，而使用Cu-水纳米流体对填充泡沫铝的腔体传热速率几乎没有影响。

3 结论

在Da=10-2的条件下，对固体骨架分别为玻璃球和泡沫铝的多孔介质方腔内Cu-水纳米流体自然对流传热进行了数值模拟，并讨论了不同多孔介质腔体在LTNE条件下的无量纲容积换热系数、Ra数、孔隙率ε和纳米颗粒体积分数对传热特性的影响。主要结论如下：

（1） 当Ra较小时，填充不同固体骨架的腔体传热速率几乎不随Nhs的增大发生变化;当Ra较大时，填充玻璃球的多孔介质腔体传热速率随Nhs增加而增加，而填充泡沫铝的腔体，Nhs的增大对传热速率几乎没有影响。

（2） 当Ra较小时，可以用LTE模型代替LTNE模型对两种不同固体骨架的多孔腔体自然对流计算;当Ra较大时，对于填充玻璃球的多孔腔体自然对流当孔隙率较大时可以采用LTE模型计算，而对于填充泡沫铝和泡沫铜的多孔腔体自然对流应采用LTNE模型计算。

（3） 对于填充泡沫铝的多孔腔体，增大ε严重降低了腔体的传热速率。对于填充玻璃球的多孔腔体，当Ra较小时腔体传热速率随ε的增大而降低，当Ra较大时腔体传热速率随ε的增大而增大。

（4） 当Ra较小时，填充玻璃球的腔体内使用Cu-水纳米流体可以明显增加腔体的传热速率。填充泡沫铝的腔体内使用Cu-水纳米流体，总的传热速率并没有明显的变化。当Ra较大时，填充玻璃球的腔体换热速率随φ的增大而降低，而使用Cu-水纳米流体对填充泡沫铝腔体的换热速率几乎没有影响。

参考文献：

［1］ NIELD D A，BEJAN A.Convection in porous media［M］.4th Edition.New York：Springer，2017.

［2］ XIE H Q，LEE H，YOUN W，et al.Nanofluids containing multiwalled carbon nanotubes and their enhanced thermal conductivities［J］.Journal of Applied Physics，2003，94（8）：4967-4971.

［3］ MOLANA M，DOGONCHI A S，ARMAGHANI T，et al.Investigation of hydrothermal behavior of Fe3O4-H2O nanofluid natural convection in a novel shape of porous cavity subjected to magnetic field dependent （MFD） viscosity［J］.Journal of Energy Storage，2020（30）：101395.

［4］ MOHEBBI R，MEHRYAN S A M，IZADI M，et al.Natural convection of hybrid nanofluids inside a partitioned porous cavity for application in solar power plants［J］.Journal of Thermal Analysis and Calorimetry，2019，137（5）：1719-1733.

［5］ SIVASANKARAN S，ALSABERY A I，HASHIM I.Internal heat generation effect on transient natural convection in a nanofluid-saturated local thermal non-equilibrium porous inclined cavity［J］.Physica A：Statistical Mechanics and Its Applications，2018（509）：275-293.

［6］ SIDDHESHWAR P G，VEENA B N.Study of natural convection with local thermal non equilibrium effects in nanoliquid-saturated low porosity enclosures［J］.International Journal of Applied and Computational Mathematics，2022，8（1）：1-20.

［7］ IZADI M，MEHRYAN S A M，SHEREMET M A.Natural convection of CuO-Water micropolar nanofluids inside a porous enclosure using local thermal non-equilibrium condition［J］.Journal of the Taiwan Institute of Chemical Engineers，2018（88）：89-103.

［8］ MEHRYAN S A M，GHALAMBAZ M，CHAMKHA A J，et al.Numerical study on natural convection of Ag-MgO hybrid/water nanofluid inside a porous enclosure：a local thermal non-equilibrium model［J］.Powder Technology，2020（367）：443-455.

［9］ TAYEBI T，CHAMKHA A J，ZTOP H F，et al.Local thermal non-equilibrium （LTNE） effects on thermal-free convection in a nanofluid-saturated horizontal elliptical non-darcian porous annulus［J］.Mathematics and Computers in Simulation，2022（194）：124-140.

［10］ 陶文铨.传热学［M］.第5版.北京：高等教育出版社，2019.

［11］ CORCIONE M.Empirical correlating equations for predicting the effective thermal conductivity and dynamic viscosity of nanofluids［J］.Energy Conversion and Management，2010，52（1）：789-793.

［12］ XUAN Y M，ROETZEL W.Conceptions for heat transfer correlation of nanofluids［J］.International Journal of heat and Mass transfer，2000，43（19）：3701-3707.

［13］ NITHIARASU P，SEETHARAMU K N，SUNDARARAJAN T.Natural convective heat transfer in a fluid saturated variable porosity medium［J］.International Journal of Heat and Mass Transfer，1997，40（16）：3955-3967.

［14］ ERGUN S.Fluid flow through packed columns［J］.Chemical Engineering Progress，1952，48（2）：89-94.

［15］ SHEREMET M A，POP I，NAZAR R.Natural convection in a square cavity filled with a porous medium saturated with a nanofluid using the thermal nonequilibrium model with a tiwari and das nanofluid model［J］.International Journal of Mechanical Sciences，2015（100）：312-321.

Study on natural convection of Cu-water nanofluid in

a square porous cavity under LTNE condition

LIU Chenxi，MA Bingshan，WANG Gang

（School of Civil Engineering，Lanzhou University of Technology，Lanzhou 730050，China）

Abstract

Using the local thermal non-equilibrium assumption，a numerical study is conducted on the natural convection of Cu-water nanofluid in a porous square cavity with solid matrix of glass beads and foam aluminum，respectively.The effects of dimensionless interphase heat transfer coefficient，Rayleigh number，porosity，and nanoparticle volume fraction on the heat transfer characteristics on the natural convection heat transfer characteristics of nanofluid in porous square cavity are investigated.The results show that the local thermal equilibrium model can replace the local thermal non-equilibrium model to calculate the natural convection inside a porous cavity when the Rayleigh number is low.When the Rayleigh number is high，for the natural convection in the porous cavity filled with glass beads，the local thermal equilibrium model can be used to calculate the heat transfer when the porosity is high，while the local thermal non-equilibrium model should be used to calculate the heat transfer for the porous cavity filled with foam aluminum.When Cu-water nanofluid is used in the cavity filled with foam aluminum，the overall heat transfer rate remains unchanged.For the cavity filled with glass beads，the use of Cu-water nanofluid can significantly increase the heat transfer rate when the Rayleigh number is low，while the heat transfer rate of the cavity filled with glass beads decreases with the increase of the volume fraction of nanoparticles when the Rayleigh number is high.

Key words

Nanofluid;Porous medium;Natural convection;Local thermal non-equilibrium

（本文责编：毛鸿艳）